Entregatze epea: martxoak 31, asteazkena, laborategi horretako ordua ere erabil daitekelarik praktika egiteko.

==== WEKA formatoko datubaseak: kurtso guztian zehar eta praktika guztietarako erabil itzazu ====

== Gomendioa: galdera enuntziatuak ez dira motzak. Lehenengo irakurri, osoki. Eta gero, joan pausuz pausu egiten, jarraitzen esandakoa ==

 

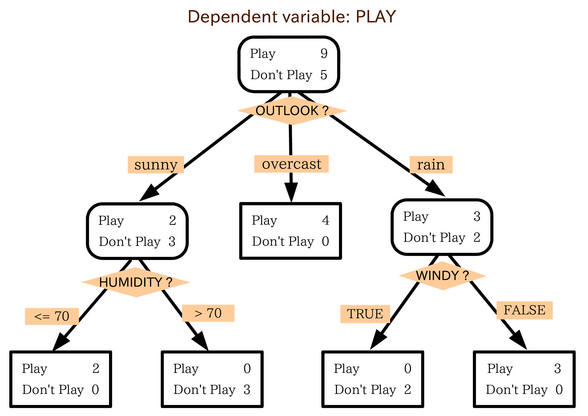
[Galdera 1 -- Sailkapen zuhaitzak -- Inausketa ("pruning") egin edo ez] -- WEKA formatoan dagoen eta 300 kasu baino gehiago dituen datubase bat aukeratu ariketarako (baina ezta ere haundiegia ez dena arbola ikus ahal izateko pantailan, arbola haundiegia izan ez dadin ere). WEKA-ren C4.5 metodoarekin (WEKA-n J48 izena du) bi sailkapen zuhaitz eraiki:

• inausketa egiten duen zuhaitza
• inausketa egiten ez duen zuhaitza

J48-ren "unpruned" parametroak inausketa aktibatu edo desaktibatzen du. Kasu guztiekin eraikitako bi arbolen bertsio grafikoak ikusiz ("Result list"-en propiedadeak), erantzun:

• eraikitako bi arbolak desberdinak al dira? ze neurriraino? tarteko aldagai askotan? hosto kopuruan? Komentatu diferentzi kualitatiboak.
• arbola bakoitzarako, erantzun: nodo kopurua (tarteko aldagai edo partizio kopurua), hosto kopurua. Datubasearen aldagai prediktore original guztiak agertzen al dira arboletan?
• zer uste duzu agertzen dutela dutela hostoetako zenbakiak? Dezimalak ahaztuz, batu itzazu hosto bakoitzean ezkerreko parteko zenbakia. Zer izan daiteke (ahaztuz dezimalak) eskubiko zenbakia hosto bakoitzean?

 

 

[Galdera 2 -- Bi sailkatzaileen asmatze tasak konparatu ------ Hipotesi testak ------ J48-ez-inausiz vs J48-bai-inausiz] -- WEKA bezalako software baten abantaila problema berezi batentzako sailkatzaile desberdin askoren asmatze tasak konparatzean datza, onenarekin geratzeko (adibidez). Sailkatzaileen asmatze tasak kalkulatzeko hainbat metodo daude. Horietako metodo bat "H metodoa" ("Hold-out") da (ikusi klaseko apunteak).

Pentsa dezagun datubase batetan J48-ez-inausiz eta J48-bai-inausiz sailkapen zuhaitzak konparatzeko, BEHIN estimatzen dugula bakoitzaren asmatze tasa H-metodoaren bidez exekuzio bakarrarekin ("Percentage split, 66% for training"), eta bi estimazioetatik onena daukanarekin geratzen gara ("Correctly Classified Instances"):
  - zer pentsatzen duzu honi buruz?
  - justua iruditzen al zaizu H-metodoaren exekuzio bakar batekin erabakitzea zein den bietako sailkatzailerik "onena"?

Argi dago H-metodoaren ("Hold-out") bidez asmatzen tasaren estimazioa hobetu daitekela bera hainbat aldiz exekutatuz, training-test banaketa egiterakoan erabiltzen den "hazia" ("seed") aldatuz ("More options"). Proposatzen dizuet sailkatzaile berezi batentzat 5 aldiz exekutatzea H-metodoa eta bere asmatze tasaren estimazioa izango da 5 exekuzio hauen tasaren batazbestekoa (+/- desbiazio standard-a). [ikus klaseko gardenkiak]

Laborategian esplikatuko dizuet bi batazbesteko hauek erabili beharrean bi sailkatzaileak konparatzeko (eta erabakitzeko bietatik zein den onena, asmatze tasa handienekoa), batazbesteko onena duena kontutan hartzea ez dela nahikoa. Bi batazbesteko konparatzea baino teknika hobeak daude: konparaketa estatistiko bat egingo dugu, test-ez-parametriko bat erabiliz (Mann-Whitney test-a) H-metodoaren 5 exekuzio hauen asmatze tasak erabiliz (ikus ezazu probako SPSS softwarearen probazko fitxategi hau).

Aukera ezazu WEKA formatoko datubase bat, 300 kasu baino gehiagokoa, ETA JOKUA EMATEN DIZUNA KONPARAKETA HAU EGITEKO (hau da, exekuziotik exekuziora asmatze tasak alda daitezela). Konparaketan, sailkatzaile bakoitzaren asmatze tasa estimatzeko, J48-ez-inausiz H-metodoaren 5 exekuzio eta J48-bai-inausiz H-metodoaren 5 exekuzioen artean egingo dugu.

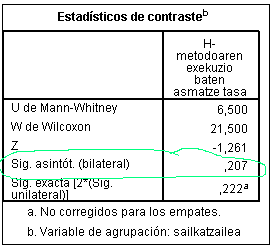
Edozein konparaketa estatistiko bat egiterakoan (gure kasuan "Mann Whitney" test-arena), test-aren "significancia asintótica"-n edo "p-value"-n (edo test-aren "esangarritasuna") dago gure galderaren erantzunaren oinarria, hau da, ea sailkatzaile bietako bat ote dagoen bestearen gainetik (irabazle / galtzaile). Bi zenbaki multzo konparatu ditugu, bakoitza 5 zenbakitakoa. "Esangarritasun asintotiko"-aren nere esplikazio intuitiboa ondokoa da:

• probabilitate bat da, 0 eta 1 artekoa. Kontuz!!! SPSS-aren irteeran komaren ezkerrean "0"-a ez da agertzen. Hobeto ulertzeko, probabilitate hori ehunekoetara (%) pasa.
• "Esangarritasun asintotiko"-ak adierazten digu konparatu ditugun bi zenbaki multzoek zenbateko "berdintasun-antzekotasun maila" duten.
• "Esangarritasun asintotiko"-aren beste definizio pixka bat zailagoa ondokoa da: konparatu ditugun bi zenbaki multzoen artean dauden diferentziak esplikatzeko, "azarrak"-"zoriak" duen pisua.
• "Esangarritasun asintotiko" honen balio %5-a baino txikiagoa bada, onartzen da konparatu ditugun bi sailkatzaileen artean diferentzi handia ("esangarria") dagoela → orduan, onartzen da H-metodoaren 5 exekuzioen asmatze tasen batazbesteko onena duen sailkatzailea HOBEA DELA ESTATISTIKOKI, eta sailkatzaile IRABAZLE batetaz hitzegin dezakegula.
• %5-eko muga hau estatistikaren muga klasiko bat da, arbitrarioa ere bai. Baina "Esangarritasun asintotiko"-aren maila %5-a baino handiagoa bada, eta nahiz eta konparatutako asmatze tasak berdinak ez izan, ezin dezakegu hitzegin sailkatzaile irabazle/galtzaile batetaz ("ezin gara busti").

Guzti hau ikusita, zein ondorio ateratzen dituzu egindako J48-ez-inausiz vs J48-bai-inausiz egindako konparaketaz H-metodoaren 5 exekuzioetan oinarrituta?

Hipotesi nuloa: J48-ez-inausiz-ren asmatze tasa ≈≈ J48-bai-inausiz-ren asmatze tasa Hipotesi alternatiboa: aurrekoa ez da egia. Beraz asmatze tasaren batazbesteko handiena duena, beste sailkatzailearen baino asmatze tasa hobea du (hau oinarri estatistiko batekin esan daiteke) p-value edo significancia asintótica ≈≈ Hipotesi nuloaren "pisua"-"sinesgarritasuna"

 

Badago noski software librea hipotesi test-ak ezagutzeko. SPSS erakutsi dizuet estatistikako "klasiko" bat delako, EHU-k bere lizentzia ordaindua duelako, eta zientziaren arlo askotan erreferentzia delako: medikuntzan, psikologian... Horrela, beste bi alternatiba hipotesi testak egiteko, non ikusi ditugun kontzeptu guztiak mantentzen diren, oso antzeko nomenklaturekin:

• WINKS softwarea (Fakultateko ordenagailuetan ere badago)
• EEBB-ko Vassar College-ren ondoko web orrian, on-line egin daitezke test estatistiko asko. Mann-Whitney test-a "ordinal data"-ren barruan dago ("value of n for sample A", esan nahi du konparatuko dugun lehen multzoaren zenbaki kopurua (gure kasuan 5). "value of n for sample B", berdin. Gero, "raw data" sartu ("Data entry" -- "Raw data for sample A", "Raw data for sample B") (datu gordinak, zure asmatze tasak, WEKA-k ematen dizkizunak H-metodoaren estimazio bakoitzean), eta "raw data"-tik kalkulatu beharko da. "Raw data" ≈ datu gordina ≈ "dato en crudo".
  Egindako test-aren esangarritasun estatistikoa ("significancia asintótica") "P₍₂₎" zutabean-balioan topatuko dugu ("p-value").

 

[Galdera 3 -- Naive Bayes sailkatzailea] -- Sinplea bere estrukturan baina asmatze-tasa handitakoa da Naive Bayes sailkatzailea. Ikerlari batzuk ere badiote: "Idiot Bayes: not so stupid after all". Gogoratu bere teoria: ikusi bere asuntzio nagusia dela aldagai prediktoreak, klasea ezagututa, beraien artean independienteak direla. Hortaz erabiltzen dituen estatistikoak p(C=c|X₁=x_1, X₂=x_{2, ...,} X_n=x_n) kalkulatzeko: p(X_i=x_i|C=c) eta p(C=c). Asuntzio hau erabiltzen du kasu berri batentzat, klase posible bakoitzarentzat kalkulatzeko bere "a-posteriori" probabilitatea, "p(C=c|kasu_berria)=p(C=c|X₁=x_1, X₂=x_{2, ...,} X_n=x_n)".

Goazen ariketa bat egitea "Hepatitis.arff" datubasearekin: lehenengo hau ireki textu editorearekin eta ulertu problemaren natura (klasearen balio posibleak, aldagai iragarle batzuk...). Goazen bakarrik bere ondoko aldagaiekin lan egitea: "fatigue" (nekea), "malaise" (ezinegona, "malestar"), "anorexia", "spleen_palpable" (ea bare-organoa  -"bazo" gazteleraz-  puztuta dagoen eta ikutu daiteken); eta noski, klasea - gaixoaren pronostikoa ("die" edo "live" balioak ditu, hau da, gaixoa hil edo bizirik dirau). Beste aldagai guztiak ezabatu itzazu (preprocess -- aukeratu eta remove). Geratu den aldagai bakoitzaren gainean klikatuz, ulertu itzazu histogramak eta bere koloreak ("Preprocess" leihoan, behe eskubi partean).

Orain, 4 prediktore horiek erabiliko ditugu "Klasea (die, live)" predizitzen saiatuko den Naive Bayes sailkatzaile bat sortzeko, aukeratu WEKA-n: "Classifier -- Bayes -- NaiveBayesSimple". Sailkatzailea eraiki eta saiatuko gara ulertzen "Classifer output" eskubiko partean agertzen zaiguna, hau da, Naive Bayes sailkatzaileak erabiltzen dituen estatistikoak. Output horren parte bat hartuko dut eta esplikatuko dut, eta honen antzekoa izango da (eskubiko parteko irudia naive Bayes-en beste problema batentzako irudia da soilik, besterik ez):

=== Classifier model (full training set) === Naive Bayes (simple) Class DIE: P(C) = 0.21019108 Attribute FATIGUE no yes 0.08823529 0.91176471 .................................................

Lehenengo, klase bakoitzaren "argazki" bat ateratzen digu, datubaseko kasu guztientzat, sailkatzailea bera. Lehenengo, "Die" klasearen a-priorizko proportzioa datubasean (output-ean beherago dago "Live" klasearen output-a). Gero, X _i aldagai prediktore bakoitzarentzat, "p(X_i=x_i|C=c)" estatistikoen balioak erakusten dizkigu. Adibidez, "Class=Die" kasuentzako, "nekea" ("Fatigue") somatu duten probabilitatea 0.911 da, p(Fatigue=yes | Class=Die) = 0.911, eta "nekea" somatu ez dutenen proportzioa p(Fatigue=yes | Class=Die) = 0.0882 da (bien batura 1 izatea, ez da?). Estatistiko eta proportzio guzti hauek datubasetik kalkulatuak izan dira!! Hepatitis.arff-ren 155 kasuetan!! Ez ditu asmatu!! Eta hauek erabiltzen ditu kasu berri bat sailkatzeko. Ateratako "Classifier output"-aren gainean, markatu ezazu zein den "p(X_i=x_i|C=c)" bakoitza. 

 Saiatu guzti hau ulertzen, eta demagun kasu berri bat etortzen zaigula (156. kasua: zergatik diot hau??), non medikuak ez dakien zein den bere klasea (ez dago zihur pronostikoa egiterako orduan), eta erabakitzen da ikasitako NaiveBayesSimple sailkatzailea erabiltzen dugula kasu hau sailkatzeko (pronostikoa egiteko). Kasu berria demagun ondokoa dela:

Fatigue = yes; Malaise = yes; Anorexia = yes; Spleen_palpable = yes

Egin eskuz naive Bayes-en lana, eta kalkulatu klase bakoitzaren "p(C=c|kasu_berria)" (hau da, bai C=Die eta bai C=live- rentzako). Zein da naive Bayes-ek egiten duen apostua, predikzioa? Gogoratu klaseko apunteak eta teoria. Ulertzen al da naive Bayes-en logika eta funtzionatzeko forma?

Egin berbera ondoko beste kasu honentzat, kalkulatuz naive Bayes-en formula erabiliz, kasu berriaren "p(C=Die|kasu_berria)" eta "p(C=Live|kasu_berria)":

Fatigue = no; Malaise = no; Anorexia = yes; Spleen_palpable = no

Nolakoa uste duzu izan beharko zela guztiz garrantzigabekoa klasea predizitzeko, eta bi balio dituen den prediktore bat (adibidez, demagun X_i aldagai boolearra dela ea "Donostian euria egin duen ala ez")? Nolakoak uste duzu izango zirela bere "p(X_i=x_i|C=c)" estatistikoak klasearen balio bakoitzarentzat (C=Die, C= Live)?

 

[Galdera 4 -- Testu zientifiko baten ulermena eta laburpena ----- k-dependence Bayesian classifier (k-db)] -- Stanford Unibertsitateko Mehran Sahami ikerlariak 1996-an "Learning limited dependence Bayesian classifiers" lana publikatu zuen. Ez da kasualidadea Stanford-eko Unibertsitatekoa: bere informatika fakultatetik data-mining-eko ikerlari onentsuenak atera dira, hala nola Google, Ebay edo HP bezalako konpainiak. 
Artikulu honetan, klasean ikusitako "K-Mendekotasuneko Sailkatzaile Bayestarra" (k-dependence Bayesian classifier) aurkezten du era ulerterraz batetan. Lehenengo, momentu horretararte ezagutzen ziren sailkatzaile Bayestarrak gogoratu (naive Bayes eta sare Bayesiarrak orokorrean), gero bere proposamena aurkeztu (k-db), hainbat datubasetan testatu bere teknika eta konparatu, bukatuz testuan erabilitako erreferentzia bibliografikoekin. Testu hau "klasiko" bat da adimen artifizialean, eta sailkapenaren munduan. Ideia sinplea baina logika handikoa.
Artikuluaren pdf-a bilatu Internet-en.
Egin ezazu artikuluaren laburpen bat (orri batekoa, bi orritakoa gehienez), jarraituz artikuluak dituen atalak ("sections") laburpena idazteko.

 

[Galdera 5 -- k-db erako estruktura Bayestarrak sortzen WEKA-rekin, eta ulertzen] --  WEKA-n ez dago zehatz-mehatz Sahami-ren "k-db" teknika berdin berdina inplementatuta. Ordea, "Bayes" sailkatzaile gainbegiratuen familiaren barruan, "BayesNet" sailkatzaileak aukera asko ematen dizkigu. Bere parametroak ikus itzazu klikatuz negritaz dagoen bere izenaren gainean. Parametro horietako bat da "search algorithm" da: honen bidez, era eta konplexidade desberdin askotako estruktura Bayestarrak "bilatu" ("search") daitezke.
"Search" parametro honen aukeretako bat "K2" teknika da (Himalaya-ko mendi tontor ezagunari omenaldia eginez, hau da, pausuz pausu sortuko bait du soluzioa, "greedy" eran).  K2 teknika honek sare Bayesiar eta sailkatzaile Bayesiar mota desberdinekoak eraiki dezake.
Horretarako, K2-ren parametroak ikus itzazu bere izenaren gainean klikatuz. Horietako bat "maximum number of parents" da. Ikusi parametro honen explikazioa:

 

Hau da, beti dependentzi gezi bat jartzen du klasea eta aldagai iragarle guztien artean. Hortik aurrera, "maximum number of parents" parametroari 2-ko balioa emanez, "zuhaitzera zabaldutako naive Bayes" ("tree augmented naive Bayes") estrukturak sor daitezke. Eta parametro honi 3 edo balio altuagoak emanez, k-db (k-menpekotasuneko sailkatzaile Bayesiarra) erako estrukturak.

Hurrengo lanak egiteko "Hepatitis.arff" datubasea aukeratu.

K2 algoritmoa aukeratuta, "Maximum number of parents" parametroari 2-ko balioa emanez, "zuhaitzera zabaldutako naive Bayes" ("tree augmented naive Bayes") estruktura sor ezazu. Aukeratu eta eraiki ezazu dagokion sailkatzailea. Eraikitako estruktura grafikoa (hau da"zuhaitz" estruktura) ikus ezazu "Result list"-en propiedadetan ikusiz bere "Visualize graph". Ohartu zaitez eraikitako grafo-estrukturaz, non, klase aldagaiak kondizionatzen ditu aldagai iragarle guztien balioak: eta gero zuhaitz erako estruktura eraikitzen duen aldagai iragarleen artean (hau da, aldagai iragarle bakoitzak beste aldagai iragarle bat du gehienez guraso bezala estrukturan -- klaseaz aparte).

"Malaise" ("ezinegona") aldagaiaren-sintomaren gainean klikatuz gero, ondoko pantalla atera beharko zaigu:

 

Atera zaigun taula, "Probability Distribution Table for MALAISE", ezinbestekoa da ulertzea. Taula horretan, sailkapena egiteko ezinbestekoak diren hainbat probabilitate daude. "Malaise" aldagai iragarlearen probabilitate banaketaren "argazkia" da, estrukturan dituen bi gurasoen kondizio-pean ("Class"-klasea eta "Fatigue": ikusi ezkerreko partea). "Malaise" aldagaiaren probabilitate banaketa agertzen da, bere gurasoen balio konbinaketa guztientzako: horregatik, lau probabilitate banaketa daude (ohartu ilara bakoitzean bi probabilitateen batura 1 dela), guraso bakoitzak bi balio posible dituelako. Horrela, adibidez:
    p(Malaise=no | Class=die , Fatigue=yes) = 0,242             p(Malaise=yes | Class=die , Fatigue=yes) = 0,758
Eman itzazu falta diren beste 6 probabilitateak, zehaztuz bakoitza zein aldagai eta baliori dagokion.

Dauden 4 probabilitate banaketak ("Probability distribution Table"-ko 4 ilarak) kontutan hartuz, horietako zeintzuk izan dute eragin gehiago K2 algoritmoak erabakitzeko dependentzi geziak "Class" eta "Fatigue"-tik "Malaise"-ra???? Azken ilara eta azken-aurrekoko distribuzio banaketak oso desberdinak dira... Zergatikan esaten da ilara bakoitza "probabilitate banaketa kondizionatu" bat dela? Nori kondizionatuta?
Noiz dugu "informazio gehiago "malaise"-ren balio posibletaz, azken ilararen kasuan (Class=live, Fatigue=yes) edo azken-aurreko ilararen kasuan (Class=live,Fatigue=no)?

 

"Maximum number of parents" parametroari 3-ko balioa emanez, "3-db" (3-mendekotasuneko sailkatzaile Bayestarra) estruktura sor ezazu, non aldagai iragarle batek gehienez 3 aldagai guraso izan ditzake estrukturan, bere balioak kondizionatzen dituztenak (WEKA-rentzat beti, guraso horietako bat klasea da). "Result list"-en propiedadetatik bere estruktura ikus ezazu ("Visualize graph").
Ohartu zaitez "Bilirubin" aldagai iragarleak 3 guraso dituela: Class, Anorexia eta Varices (gibelean barizeak izan edo ez, zain puztuak). Bilirubinaren balio altua izatea ez da izaten sintoma ona medikutzan... "Bilirubin" nodoan (aldagaian) klikatu eta bere "Probability Distribution Table" erakutsi. Lehenengo, taula ikusiz (zutabetako balioak), ohartu zaitez WEKA-k erabaki duela bi balio diskretotan diskretizatzea "Bilirubin"-en balio jarraiak (-infinitotik 1'65-ra; eta 1'65-tik infinitora).
Erantzun ondorengo galderei, "Probability Distribution Table for BILIRUBIN"-en inguruan:
    - zenbat ilara ditu (taula honen ilara bakoitza probabilitate banaketa bat da, aldagai honen gurasoen balioetara kondizionatuta... ulertu ezazu esan dudana)? Zergatik daude esan duzun ilara kopurua?
    - emaizkidazu agertzen diren "p(Bilirubin | Class, Anorexia, Varices)" probabilitate guztiak, banan banan (adibidez, zein izango zen "p(Bilirubin=between 1'65 and infinite | Class=die, Anorexia=no, Varices=yes)" probabilitatearen balioa? (eta beste guztiena ere eman)).

---