El
Modelo SLIM
La
Ecuación del Software
La cantidad de trabajo que se encuentra en cualquier
producto se puede ver como el producto del esfuerzo realizado en un periodo de
tiempo, y se puede escribir como
Producto = (Constante) · Esfuerzo · Tiempo
donde
Producto
representa cierta medida sobre la funcionalidad del mismo, y se cree
proporcional al producto Esfuerzo · Tiempo. La medida SLOC suele ser una medida
habitual de la funcionalidad.
Esfuerzo
representa el trabajo humano, medido en personas-mes o personas-año.
Tiempo
representa la duración del trabajo, medido en meses o años.
La Constante es
un factor de proporcionalidad. Una vez establecidas las otras tres variables,
esta constante permite igualarlos. Sin embargo parece que la cantidad de producto
depende también de "cómo se hacen las cosas", puesto que con el mismo
esfuerzo y tiempo, y dependiendo del entorno de trabajo, podremos conseguir
mayor o menor cantidad de producto.
Productividad del Proceso.
La ecuación anterior tiene mayor sentido si la expresamos
como
Producto = Productividad · Esfuerzo · Tiempo
de donde podemos obtener
el valor de Productividad, si
conocemos los otros términos, como
Productividad = Producto/(Esfuerzo · Tiempo).
Aunque de esta manera la Productividad no está definida
precisamente, se supone que incluye un conjunto de factores que afectan a toda
la organización, incluyendo
• la gestión del proyecto
• la utilización de buenos requerimientos, diseños,
codificaciones, inspecciones y pruebas
• el nivel del lenguaje de programación
• el estado de la tecnología
• la experiencia de los miembros del grupo
• la complejidad de la aplicación.
En un determinado
momento del proyecto, el valor de la Productividad es fijo. Sin embargo, la
evolución en el tiempo y la acción de la dirección puede hacer cambiar su
valor. Esta productividad es un conjunto de factores y se puede denominar
"parámetro de productividad del proceso".
Refinamiento de la Ecuación Software.
Basándonos en las tendencias establecidas por la base de
datos QSM, podemos deducir que la relación entre los términos es no lineal
Producto = Parámetro de Productividad · (Esfuerzo/B)(1/3)· Tiempo(4/3)
donde
• la funcionalidad del producto se mide en SLOC
• el parámetro de productividad se obtiene por calibración
de proyectos ya realizados
• esfuerzo es el trabajo en personas-año
• B es un factor de destreza especial que es función del
tamaño. Se incrementa ligeramente de las 18.000 a las 100.000 SLOC, como se
muestra en la tabla 2.1.
Esta ecuación se obtuvo inicialmente mediante el análisis
de una docena de grandes proyectos software de la década de los 70.
Justificación de las potencias 1/3 y 4/3.
Es importante la validación de esa relación potencial,
puesto que en ocasiones el resto de los factores se suponen constantes, y la
ecuación software queda como
Esfuerzo = Constante/Tiempo4.
Se observa que pequeños cambios en el tiempo de
desarrollo provocan grandes modificaciones en el esfuerzo. Por ejemplo,
extendiendo el tiempo de desarrollo de 18 meses a 19 meses (5.5% más),
disminuye el esfuerzo en un 19.5%.
Empíricamente se validó esta relación posteriormente con
70 sistemas más. Después, a mediados de los 80 se utilizaron 750 sistemas. El
método de validación fue el de reordenar la ecuación como
Esfuerzo = [tamaño · B1/3/Parámetro de productividad]3 · (1/Tiempo4).
Para un sistema concreto, los términos entre corchetes
son constantes. Se buscó en la base de datos clases para los que el factor
entre corchetes era parecido, encontrándose 8 grupos. Para cada grupo se buscó
esa relación potencial, tal como se muestra en la tabla 2.2. En la figura 2.1.
se muestra el ajuste para el mayor subgrupo (G). El valor medio del exponente
para los ocho grupos es de 3.721 con una desviación estándar de 0.215. La
probabilidad que el valor real del exponente esté entre 3.5 y 4.5 es del 84%.
Con estos datos, y por razones prácticas se concluyó que el exponente de 4 era
un valor razonable en esa ecuación.
El parámetro de la productividad del proceso
Se obtiene calibrando sistemas terminados. Por ejemplo,
dado un sistema de 30.000 líneas de Cobol, finalizado en 17 meses con un gasto
de recursos de 146 personas-mes, tenemos
Parámetro de productividad = (SLOC)/(Esfuerzo/B)(1/3) · Tiempo(4/3) =
= 30.000 /(12.17/0.28)(1/3) (1.42)(4/3).
El
índice de productividad.
El índice de productividad (PI) es una escala de enteros asociada a los valores del PP obtenidos para la base de datos QSM (Tabla 2.3). Este PI se comporta exponencialmente (ver figura 2.2) siendo el valor factor multiplicador de un índice al siguiente de 1.3.
Rango
del índice.
El PI y el PP constituyen una macromedida del entorno general de desarrollo. Valores bajos se asocian a entornos elementales y herramientas inadecuadas, o a un alto grado de la complejidad del producto (como microcódigo o firmware). Valores altos se asocian a buenos entornos, personal experimentado o a productos de baja complejidad que se comprenden bien. El PI medio se extiende desde 2 a 16 (para los 11 tipos de aplicación).
Valoración
económica.
Dado que el PI representa el PP exponencial, una pequeña mejora en este índice tiene gran importancia económica, como se muestra en la tabla 2.4 para el anterior sistema en Cobol. Otro ejemplo se muestra en la tabla 2.5.
Productividad
convencional.
El PP tiene un significado más complejo que la medida de productividad en SLOC (personas-mes) puesto que es la medida de la efectividad en el desarrollo de software en una organización o proyecto.
Utilización de la Ecuación para Estimación.
La utilización básica es la de estimar tiempo y esfuerzo
al comienzo de un nuevo proyecto software. Se deben conocer el PI (y el PP) a
través de proyectos anteriores. Quedan dos incógnitas en la ecuación. Se puede
resolver como
• solución determinista
• simulación
• programación lineal
Solución
determinista
Consisten en poner la ecuación como sigue
(esfuerzo/B)1/3 · tiempo4/3 = SLOC/PP
y añadir una segunda
ecuación basada en la "tasa de acumulación de esfuerzo humano", y se
expresa como el parámetro de acumulación del esfuerzo":
esfuerzo total acumulado/tiempo3 = parámetro MBP.
Para un proyecto ya acabado es fácil obtener este
parámetro calibrado. El MBP (con su MBI asociado) permite establecer un
"tiempo mínimo de desarrollo"
Simulación
Montecarlo.
Consiste en incorporar la incertidumbre tanto en el
tamaño SLOC como en el MBI. Se simula mediante el método de Montecarlo desde
100 a 1000 veces, calculándose después la media y la desviación típica.
Programación
lineal.
Se pueden aplicar al proceso de estimación cinco
restricciones
• máximo MBP
• máximo pico de esfuerzo
• mínimo pico de esfuerzo
• plazo de entrega
• presupuesto monetario para el desarrollo
Estas restricciones se pueden expresar en términos de
esfuerzo total (K), tiempo de desarrollo (td), y personas-año/año (y´), coste/persona-año medio.
Entre los extremos se encuentran soluciones de compromiso.
Modelo del Ciclo de Vida. Modelo teórico de Norden
Un modelo propuesto por para mostrar la evolución del desarrollo de un proyecto es el de Norden-Rayleigh, basado en la curva de Rayleigh (figura 3.2) cuyas ecuaciones y diferentes formas de la curva se muestran en la figura 3.3. El método de estimación de Putnam se basa en ese modelo teórico que establece el soporte para desarrollar otras hipótesis.
Acumulación de Personal
La tasa de contratación de personal en un proyecto
debiera ser igual a la tasa de necesidades del mismo.
Parámetro de acumulación
de personal.
Es claro en la curva de Rayleigh que la tasa de
contratación tiene implicaciones en td y E. Un gran incremento temprano en el
personal acorta td
.
El MBP se calcula como
.
Se calculó el MBP para toda la base de datos QSM,
considerándose seis valores representativos a los que se les asocia el índice
MBI (tabla 3.1). El efecto gráfico de este parámetro se muestra en la figura
3.5. El nivel seis representa un proyecto en el que todo el personal se
contrata al comienzo, con el objetivo de disminuir el tiempo de desarrollo.
El MBI indica que acumular personal moderadamente reduce
el esfuerzo de desarrollo, en comparación con hacerlo más intensamente. La
tabla 3.2 muestra el efecto de incrementar el MBI en un proyecto Cobol de
30.000 líneas con un PI constante de 11. Se observa que aunque es posible una
reducción del plazo, sólo se consigue con un gasto elevado. El coste o
incremento de esfuerzo entre un MBI de 1 y un MBI de 3 se muestra en la figura
3.6. Con el MBI de 1 el nivel máximo de personal es de cinco y con el de 3 es
de 12.
Mínimo
tiempo de desarrollo.
La ecuación software se puede reordenar como
tamaño/PI= esfuerzo · tiempo,
y se puede representar
según la figura 5.1. Para un proyecto dado, la relación tamaño/PI es fija,
indicando que a medida que el tiempo aumenta, el esfuerzo disminuye. Esta línea
puede ser diferente en otros proyectos.
El MBI es otra expresión del esfuerzo y tiempo
MBI = esfuerzo/tiempo3
y su línea también es
fija para un determinado proyecto: a medida que el esfuerzo aumenta, el tiempo
también lo hace. Empíricamente no se han encontrado proyectos a la izquierda de
la línea MBI, y así se ha denominado en la figura 5.2 "región imposible"
a esa zona, y se obtiene el "tiempo mínimo", que corresponde al
máximo esfuerzo.
Los tres factores subyacentes
Este tiempo mínimo es función de tres factores: el PI, el
MBI y el tamaño.
Productividad.
Para desarrollar un producto con menor tiempo y esfuerzo
es necesario mejorar el PI tal como se muestra en la figura 5.3.
Acumulación
de personal.
El sistema Cobol de 96.000 líneas (figura 5.3) se realizó
con un MBI de 3; sin embargo el MBI también afecta al tiempo mínimo de
desarrollo y el esfuerzo, como se muestra en la figura 5.4 donde, con un PI de
15, a medida que aumenta el MBI disminuye el tiempo mínimo y aumenta el
esfuerzo. En la figura 5.5 se muestran valores para el mismo proyecto con otros
PI diferentes. El MBI se obtiene por calibrado de proyectos anteriores, y
representa el entorno y estilo de gestión de la empresa.
Tamaño.
El tercer factor es el tamaño del sistema, puesto que
cuanto mayor es el sistema, más elevados son el tiempo mínimo y el esfuerzo
(figura 5.6)
Región
Imposible.
En la figura 5.7 aparece un diagrama con la "región
imposible" para el sistema Cobol de 96.000 líneas (PI=19). Las líneas
diagonales son las correspondientes al esfuerzo. La línea gruesa marca el
tiempo mínimo de desarrollo para cada tamaño del proyecto. El esfuerzo resulta
ser de 2.4 años.
La figura 5.8 muestra el mismo sistema para un PI de 11.
El tiempo mínimo es ahora de 2.2 años, y el esfuerzo es de 28 personas-año. La
región imposible representa estrategias de personal inalcanzables, puesto que
por diversas circunstancias, no se puede acelerar el desarrollo de software
todo lo que uno quiera.
Interpretación analítica del
modelo Norden-Rayleigh de distribución del esfuerzo
K es el esfuerzo total en personas-año de todo el proyecto (no sólo del desarrollo). El esfuerzo acumulado C(t) es nulo al comienzo y se va acercando hacia K. La tasa de variación de este esfuerzo acumulado dC/dt representa el número de personas involucradas en el desarrollo en cualquier punto de tiempo m(t). El esfuerzo acumulado es
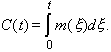
Una asunción de Norden
es que el número óptimo de personas para el proyecto en un momento dado es
proporcional al número de problemas a ser resueltos, de donde
con k factor de proporcionalidad. La efectividad para resolver
problemas aumenta a medida que el proyecto avanza. Este factor se representa
por p(t)
que resolviéndola queda
.
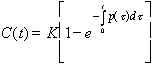Norden asumió que la función de aprendizaje p(t) era
lineal p(t)=2at, y entonces
El nivel de personal m(t) se obtiene diferenciando la
ecuación anterior
Derivando m(t) e
igualando a cero podemos obtener la relación entre el tiempo en el que el nivel
de personal es máximo y el parámetro a
y sustituyendo el valor
de a encontramos el máximo nivel de personal
.
Relación
con la ecuación software.
La ecuación software nos da el esfuerzo E y el tiempo td. Empíricamente Putnam observó que el
pico de personal estaba muy cercano al tiempo de desarrollo del sistema, que
denominó td. td también es la fecha en la que el sistema está
completamente operativo. En la ecuación de Rayleigh, a establece la forma de la ecuación y está relacionado con el td como
sigue
.
E representa el esfuerzo
hasta td, y las relaciones de la figura 3.3
dan
K = E/0.39.
Con K y td ya establecidos, la ecuación de
Rayleigh se convierte en una expresión en esfuerzo y tiempo (y' y t)
.
Dificultad.
La pendiente de la distribución del personal tiene varias
propiedades. Diferenciando m(t)
para t = 0
El cociente 
se denomina
"dificultad". Un proyecto es más difícil cuando la demanda de
personal elevada o cuando el plazo es corto.
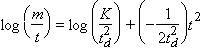(figura 4.2)
D está relacionda también con el nivel máximo de personal
m0 y td
.
Si el plazo es corto, el coeficiente de Norden a es alto y m0 proporciona un valor más elevado, lo
que implica mayor número de personas.
Acumulación de personal.
Vamos a ver la sensibilidad de D con respecto a K y td:
D'(K) es siempre menor que D'(td), y quiere decir que el desarrollo de
software es sensible al plazo.
Putnam observó que D'(td) tenía gran importancia y constató
que si el esfuerzo se incrementa, el tiempo también lo hace, de tal manera que 
permanece constante
alrededor de un valor. Esta cantidad se representa por 
. (
es el MBP o parámetro de acumulación de personal)
El MBP (
) tiene gran influencia en la forma de la distribución del
personal. Cuanto mayor sea 
, más apuntada será la distribución y más rápida la
acumulación de personal. 
es la
"acumulación de personal" (figura 4.3).
Coste acumulado de
personal.
El esfuerzo (coste) de personal en la fecha de entrega td
se obtiene poniendo t = td.
.
Esto quiere decir que una vez que se ha entregado el
sistema sólo se ha gastado el 39% del esfuerzo total, en el que se incluyen
modificaciones y mantenimiento. En td,
m(t) tiene un máximo, con un valor
Productividad vs
Dificultad.
Dibujando (en escalas logarítmicas) la
"productividad de desarrollo" y la "dificultad" de cada
proyecto como en la figura 4.6 se sugiere una relación tal como
donde
y Cn es una constante de proporcionalidad
que depende del entorno. En este modelo Pr no es utilizable directamente.
La ecuación software
Como el tamaño del
producto S es
S = productividad · 0.39K
donde la productividad =
tamaño/esfuerzo. Previamente se definió
de donde
y sustituyendo D
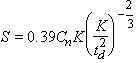de donde
0.39Cn
se remplaza por el coeficiente PP o parámetro de productividad (inicialmente
denominado Factor Tecnológico)
Un
Método Simple de Estimación
Es aplicable sólo a medios y grandes proyectos, y las
condiciones a cumplir son:
• más de 5000 líneas de código
• más de 6 meses de tiempo de desarrollo
• esfuerzo de más de 18-20 personas-mes
• el máximo nivel de personal es mayor de 3 personas.
Calibrado.
Se trata de obtener el PP de la organización.
1) Se introduce el factor B puesto que le tamaño afecta
al PP.
La figura 14.1 ilustra los términos. B se obtiene de la
tabla 2.1.
2) Se elige de la tabla 2.3 el valor del PP más cercano
al obtenido en 1)
Tamaño.
Se puede estimar bien en la fase de requerimientos o en
la fase de análisis funcional.
Requerimientos.
a: mínimo tamaño posible (SLOC)
b: máximo tamaño posible (SLOC)
Tamaño esperado=(a+b)/2
Desviación típica = (b-a)/6
Análisis funcional.
Para cada subsistema (considerar de 3 a 10 subsistemas)
a: tamaño mínimo posible
m: tamaño probable del subsistema
b: tamaño posible máximo
Tamaño esperado en F
F = (a + 4m + b) / 6
Desviación típica
SD = (b - a) / 6
Tamaño esperado del sistema completo = F1 + F2 + ... + Fn
con
Estimaciones.
Tiempo mínimo de desarrollo:
Esfuerzo máximo:
Fecha de pico de personal:
tpicoMP = fracción · td-min
la fracción se obtiene de la tabla 14.1.
Pico de personal.
Personal medio.
Planes del personal.
En las figuras 14.2A, 14.2B, 14.2C, 14.2D se muestran
cuatro posibilidades de nivel de personal de acuerdo con el tamaño del proyecto.
Las escalas están normalizadas con respecto al valor medio del personal y al
td. 1.0 en la escala vertical representa el personal medio.
Estudio de viabilidad
No hay fórmula empírica para determinar las necesidades
de personal, pero se puede considerar y´feas = 1 a 5.
Efeas = y´feas · td-min/4.
Análisis funcional (figura 14.4).
El esfuerzo es una fracción del esfuerzo de desarrollo,
como se indica en la tabla 14.2
Efunc = fracción (E).