Validez
de las Predicciones en la Estimación de Costes
Javier Dolado © dolado@si.ehu.es
(5-Enero-1999)
Trabajo realizado con apoyo de los proyectos CICYT TIC98 1179-E
y UPV-EHU 141.226 EA083/98
Introducción
De todos es sabido que una buena estimación inicial del coste
de un proyecto es una de las mayores necesidades en la gestión del
proyecto. Existen diversos métodos para realizar estimaciones iniciales
del esfuerzo de desarrollo, y casi todos ellos utilizan datos de proyectos
anteriores para calcular las nuevas predicciones. Nos podemos imaginar
que, dependiendo del método utilizado, obtendremos mejores o peores
resultados. Se han utilizado diversos métodos en la estimación,
comenzando por la regresión clásica, razonamiento basado
en casos, redes neuronales, programación genética y otros.
Aunque existen diferencias entre los mismos, y unos métodos funcionan
mejor que otros, todavía no se puede decir que exista un procedimiento
notablemente superior al resto. La elección de uno u otro método
de estimación se realiza según las características
del entorno de estimación (experiencia con los métodos, etc.)
y según los valores que proporcionan determinadas variables estadísticas.
En los párrafos siguientes se definen las variables más habituales
para evaluar los resultados..
Algunas medidas muy comunes, tales como el coeficiente de correlación
y el coeficiente de determinación R2, pueden dar una
idea equivocada sobre las capacidades predictivas del modelo de estimación
en cuestión. Por lo tanto, se debieran examinar también medidas,
claramente predictivas, como son el Nivel de Predicción y la Magnitud
Media del Error Relativo. Aunque no se estudiará en estas páginas,
también es una cuestión importante para la definición
de modelos de estimación la de si se utiliza una parte de la muestra
para construcción y otra para evaluación del modelo, o si
se utiliza el mismo conjunto de datos para la construcción del modelo
de estimación y para la evaluación.
Algunas medidas de la bondad de la estimación
y de la capacidad de predicción
En la literatura se suele encontrar que los criterios para determinar
la bondad de las predicciones se basa en el examen de los valores del coeficiente
de correlación y, principalmente, del coeficiente de determinación
R2 (también denominado coeficiente de correlación
múltiple al cuadrado o coeficiente de determinación múltiple).
-
Coeficiente de determinación múltiple, R2,
y R2 ajustado, son algunas medidas habituales en el análisis
de regresión, denotando el porcentaje de varianza justificado por
las variables independientes. El R2 ajustado tiene en cuenta
el tamaño del conjunto de datos, y su valor es ligeramente inferior
al de su correspondiente R2 [Norusis, 1993].
El R2 es un criterio de valoración de la capacidad de
explicación
de los modelos de regresión, y representa el porcentaje de
la varianza justificado por la variable independiente. Se puede interpretar
como el cuadrado del coeficiente de correlación de Pearson entre
las variables dependiente e independiente, o también como el cuadrado
del coeficiente de correlación entre los valores reales de una variable
y sus estimaciones. Si todas las observaciones están en la línea
de regresión, el valor de R2 es 1, y si no hay relación
lineal entre las variables dependiente e independiente, el valor de R2
es 0. El coeficiente R2 es una medida de la relación
lineal entre dos variables. A medida que su valor es mayor, el ajuste de
la recta a los datos es mejor, puesto que la variación explicada
es mayor; así, el desajuste provocado por la sustitución
de los valores observados por los predichos es menor.
Los valores que se han obtenido para el coeficiente R2 en
los diferentes estudios publicados, por ejemplo, sobre los puntos de función
varían desde 0,44 hasta 0,87. Apoyándose en estos valores,
algunos autores afirman la validez de la técnica de los puntos de
función. Sin embargo, es una conclusión que no se desprende
directamente de esos datos. Fijémonos que son valores explicativos,
no predictivos. Tanto el R2 como el coeficiente de correlación
no son las medidas más adecuadas para evaluar la predicción
de un modelo; en el mejor de los casos se trata de medidas del ajuste de
la ecuación a los datos, no de la capacidad predictiva del modelo.
En algunos casos la idea que nos transmite el R2 puede coincidir
con la de las variables que a continuación se muestran, pero en
otros no.
Desde este punto de vista, las variables más convenientes para
la evaluación son PRED(0,25), nivel de predicción al 25%,
y MMRE, magnitud media del error relativo, definidas en [Conte et
al., 1986], y descritas a continuación.
-
Magnitud Media del Error Relativo, MMRE, se define como
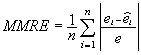 ,
donde e es el valor real de la variable, ê es su valor
estimado y n es el número de proyectos. Así si el
MMRE es pequeño, entonces tenemos un buen conjunto de predicciones.
Un criterio habitual para considerar un modelo como bueno es el de MMRE
< 0,25. La Figura 1 muestra las distancias que se utilizan para el cálculo
de esta medida.
,
donde e es el valor real de la variable, ê es su valor
estimado y n es el número de proyectos. Así si el
MMRE es pequeño, entonces tenemos un buen conjunto de predicciones.
Un criterio habitual para considerar un modelo como bueno es el de MMRE
< 0,25. La Figura 1 muestra las distancias que se utilizan para el cálculo
de esta medida.
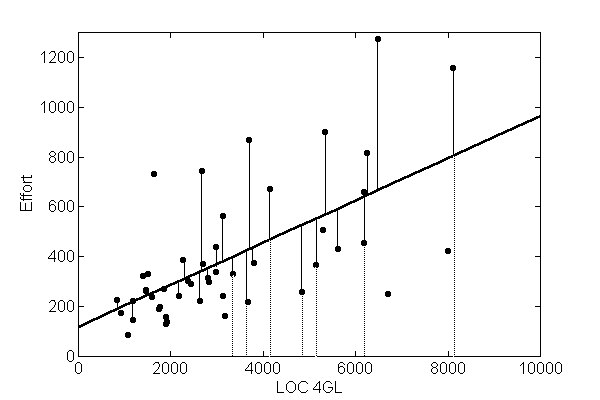
Figura 1. Distancias utilizadas en el MMRE. Las líneas continuas
representan la diferencia entre el valor real y el estimado.
-
Predicción de Nivel l -PRED(l)-, donde l es un porcentaje,
se define como el cociente del número de casos en los que las estimaciones
están dentro del límite absoluto l de los valores
reales entre el número total de casos. Por ejemplo PRED(0.1) = 0,9
quiere decir que 90% de los casos tienen estimaciones dentro del 10% de
sus valores reales; PRED(0,25) = 0,9 quiere decir que el 90% de los casos
tiene estimaciones dentro del 25% de sus valores reales. Un criterio habitual
para aceptar un modelo suele ser el de PRED(0,25) ³
0,75, aunque algunos autores rebajan este requisito. La Figura 2 representa
gráficamente el nivel de predicción.
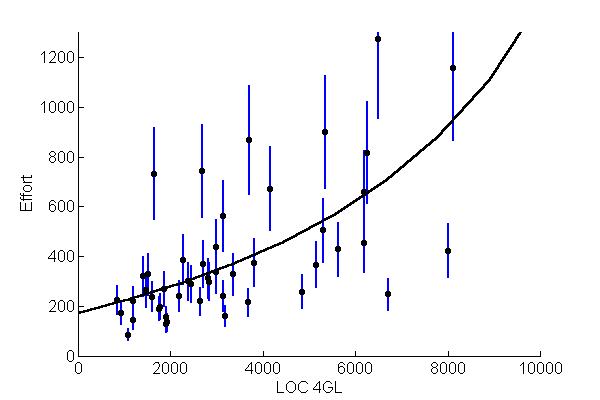
Figura 2. El nivel de predicción se calcula
sumando el número de veces que la línea continua se corta
con los trazos verticales (rango del 25% de los valores reales), y después
dividiendo esa suma entre el número total de puntos.
Volviendo a lo comentado anteriormente sobre los puntos de función
y utilizando estos dos criterios, la supuesta capacidad de predicción
de esas variables disminuye notablemente. Este es un caso donde los valores
de explicación pueden desfigurar la verdadera capacidad predictiva
[Dolado y Fernández, 1998]. Igual ocurre en algunos modelos de estimación
de costes mediante las líneas de código.
Análisis de varios conjuntos
de datos
La Tabla 1 muestra los resultados finales obtenidos para diversos conjuntos
de datos. En la columna "Valores de Explicación" aparecen descritos
el coeficiente de correlación múltiple R (Multiple R), el
R2 (R Square) -en negrita-, y el R2 ajustado (Adjusted
R Square). En la última columna se muestra la ecuación que
mejores valores consigue en el PRED(0,25) y en el MMRE. De esta manera
podemos comparar los valores explicativos con los valores predictivos.
En todos los casos observamos el "optimismo" del R2 en comparación
con las variables explicativas. Excepto en el último caso (datos
de 1997, en el J. of Systems and Software), donde el R2 presenta
un valor bajo (0,4) y unos valores no muy buenos de las variables explicativas,
en el resto de datos el R2 nos invita a pensar en buenas capacidades
predictivas, cuando lo único que tenemos es una cierta explicación.
Por ejemplo, en el primer conjunto de datos el valor del R2
de 0,84 es excesivamente bueno para después obtener un PRED(0,25)=53,4,
que no se puede considerar muy aceptable. No obstante el MMRE entra dentro
del límite de lo aceptable.
Los R2 expuestos son los que corresponden a los mejores valores
predictivos según lo denotado por las variables PRED(0,25) y MMRE,
lo que todavía nos indica que pueden existir diferencias mayores
a las presentadas en la tabla; de hecho esto ocurre, puesto que han aparecido
algunas ecuaciones de regresión con mejores valores en el R2
que los mostrados en la tabla 1.
Es curioso el caso de los conocidos datos de B. Boehm en los que una
simple regresión sobre los datos consigue unos valores predictivos
muy pobres. Sin embargo COCOMO mejora considerablemente los resultados
predicitvos, indicando que las ecuaciones de COCOMO incorporan "conocimiento"
a los datos, sobre todo a través de los multiplicadores.
Tabla 1. Valores de R2, PRED(0,25) y MMRE para diversos conjuntos
de datos
|
Origen de los Datos
|
VALORES DE EXPLICACION
|
|
ESTIMACIÓN DE LA CURVA
Y VALORES DE LAS VARIABLES DE PREDICCIÓN
|
|
Abran y Robillard, IEEE TSE, 1996
|
Multiple R .91844
R Square .84353
Adjusted R Square .82614
|
Ecuación |
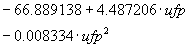
|
| |
|
Pred
(0.25) |
57.14
|
|
|
|
MMRE |
0.2339
|
|
Miyazaki et al., JSS, 1994
|
Multiple R .88005
R Square .77450
Adjusted R Square .76949
|
Ecuación |
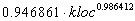
|
|
|
|
Pred
(0.25) |
42.55
|
| |
|
MMRE |
0.3999
|
|
Aproximación a los datos de Matson et al, IEEE TSE,
1994
|
Multiple R .72057
R Square .51922
Adjusted R Square .51450
|
Ecuación |
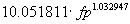
|
| |
|
Pred
(0.25) |
27.88
|
| |
|
MMRE |
0.8485
|
|
Belady y Lehman, 1979
|
Multiple R .88388
R Square .78124
Adjusted R Square .77418
|
Ecuación |
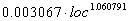
|
| |
|
Pred
(0.25) |
33.33
|
| |
|
MMRE |
0.6258
|
|
Boehm, 1981
|
Multiple R .85862
R Square .73723
Adjusted R Square .73293
|
Ecuación |
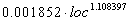
|
| |
|
Pred
(0.25) |
17.46
|
| |
|
MMRE |
1.1336
|
Conjunto de datos combinación de los de Albrecht y
Gaffney, (IEEE TSE 1983) y los de Kemerer, CACM, 1987
|
Multiple R .72805
R Square .53006
Adjusted R Square .51735
|
Ecuación |
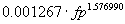
|
| |
|
Pred
(0.25) |
7.69
|
| |
|
MMRE |
1.18
|
|
Dolado, JSS, 1997
|
Multiple R .63998
R Square .40957
Adjusted R Square .39674
|
Ecuación |
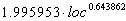
|
| |
|
Pred
(0.25) |
37.99
|
| |
|
MMRE |
0.4375
|
Conclusión
En bastantes artículos sobre modelos de estimación nos
podemos encontrar con validaciones de modelos (o de métodos) en
los que las únicas variables documentadas son el coeficiente de
correlación y el coeficiente de determinación, que son variables
estadísticas relacionadas con el ajuste a los datos del modelo especificado.
Y téngase en cuenta también que el R2 se construye
desde el punto de vista de la regresión lineal. Bien es cierto que
las transformaciones de las variables dependiente e independiente nos permiten
construir otros tipos de relaciones y seguir utilizando el R2,
correctamente, para la explicación. Pero resulta inaplicable
a otros modos de estimar como, por ejemplo, el juicio de expertos, razonamiento
basado en casos, etc.
En definitiva, lo que queremos es realizar predicciones lo más
acertadas posibles, sin importarnos el método; aceptaríamos
hasta la bola mágica, si ésta funcionara. Y para medir esa
capacidad de predicción se deben utilizar variables predictivas
principalmente, no sólo explicativas. Además, siempre
deben tenerse en cuenta la aparición de casos anómalos, la
normalidad de los datos (difícilmente conseguible, por otra parte),
la colinealidad entre variables independientes y muchas otras.
Se pueden cuestionar todavía más aspectos problemáticos
a la hora de dar validez a un modelo predictivo, y que muchas veces son
descuidados cuando se construyen, validan e, incluso, se enseñan.
Sólo una visión global de todas las variables, las de ajuste
y las puramente expresivas de capacidad de predicción nos pueden
mostrar verdaderamente las posibilidades de nuestro método y de
nuestros datos.
Referencias
-
[Conte et al., 1986] S.D. Conte, H.E. Dunsmore y V.Y. Shen, Software
Engineering Metrics and Models, Benjamin/Cummings, 1986
Es el primer libro de texto dedicado a la medición. Aunque gran
parte del texto está ya obsoleto, todavía se puede aprender
mucho en algunas de sus páginas. El capítulo dedicado al
análisis estadístico es una buena introducción a los
problemas de análisis de las estimaciones.
-
[Dolado y Fernández, 1998] J.J. Dolado y L. Fernández, “Genetic
programming, neural networks and linear regression in software project
estimation”, INSPIRE III, pp 157-171, 1998.
Se comparan diversos métodos de estimación utilizando, además,
diferentes muestras en cada conjunto de datos.
-
[Norusis, 1993] M. J. Norusis, Documentation SPSS for Windows, SPSS, Inc.,
Chicago, 1993.
Sorprendentemente, este manual de un producto comercial es uno de los textos
más didácticos sobre estadística aplicada, y sus capítulos
sobre regresión son muy claros.
Origen de los datos
Los datos utilizados en la tabla 1 se pueden conseguir en las siguientes
referencias:
A. Abran y P.N. Robillard, “Function Point Analysis: An Empirical Study
of Its Measurement Processes”, IEEE Trans on Software Engineering, Vol.
12, No. 12, December 1996, pp. 895-910
A.J. Albrecht, y J.E. Gaffney, "Software Functions, Source Lines
of Code, and Development Effort Prediction: A Software Science Validation",
IEEE Trans. Software Eng., vol. 9, no. 6, Nov. 1983.
B. Boehm, Software Engineering Economics, Prentice-Hall, 1981
J.J. Dolado, A Study of the Relationships among Albrecht and Mark II
Function Points, Lines of Code 4GL and Effort, Journal of Systems and Software,
Vol. 37, pp 161-173, May 1997
Y. Miyazaki, M. Terakado, K. Ozaki y H. Nozaki, Robust Regression for
Developing Software Estimation Models, Journal of Systems and Software,
Vol. 27, pp. 3-16, 1994
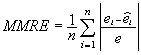 ,
donde e es el valor real de la variable, ê es su valor
estimado y n es el número de proyectos. Así si el
MMRE es pequeño, entonces tenemos un buen conjunto de predicciones.
Un criterio habitual para considerar un modelo como bueno es el de MMRE
< 0,25. La Figura 1 muestra las distancias que se utilizan para el cálculo
de esta medida.
,
donde e es el valor real de la variable, ê es su valor
estimado y n es el número de proyectos. Así si el
MMRE es pequeño, entonces tenemos un buen conjunto de predicciones.
Un criterio habitual para considerar un modelo como bueno es el de MMRE
< 0,25. La Figura 1 muestra las distancias que se utilizan para el cálculo
de esta medida.