Movimiento bajo la acción de fuerzas centrales. Conservación del momento angular
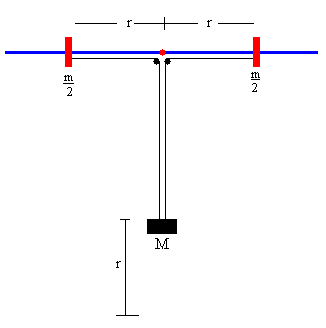
En esta página, se simula una experiencia de laboratorio que nos muestra la conservación del momento angular. Consta de una varilla horizontal que supondremos de masa despreciable que gira alrededor de un eje vertical que pasa por su centro con velocidad angular ω. A lo largo de la varilla, deslizan sin rozamiento dos masas puntuales iguales.
Las partículas deslizantes, de masa m/2 cada una, están unidas mediante cuerdas a un bloque de masa M que cuelga, tal como se muestra en la figura.
 |
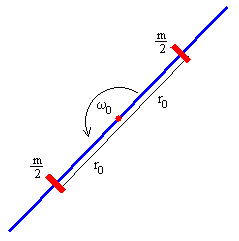 |
Inicialmente, se fijan las masas puntuales a una distancia r0 del eje de rotación y el sistema gira con velocidad angular ω0. Se liberan las masas deslizantes mediante algún dispositivo y se observa el movimiento del sistema.
Momento angular
El momento angular inicial es el producto del momento de inercia por la velocidad angular ω0. El momento de inercia es la suma del momento de inercia de la varilla que supondremos despreciable y el de las dos masas deslizantes iguales que distan r0 del eje de rotación
El momento angular, cuando las masas deslizantes se encuentran a una distancia r del eje de rotación, vale
L=mr2ω
Como las fuerzas que actúan sobre el sistema pasan por el eje de rotación. La constancia del momento angular implica que cuando las masas deslizantes se alejan del eje de rotación la velocidad angular ω disminuye y cuando se acercan ω aumenta.
Movimiento de las masas deslizantes
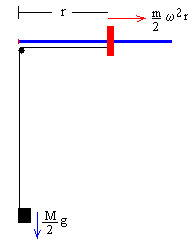 Para estudiar el movimiento de las dos masas
deslizantes y del bloque que cuelga, nos situamos en el Sistema de Referencia no inercial que gira con la varilla con velocidad
angular ω. Consideremos el sistema formado por una masa deslizante situada a
una distancia r del eje de rotación y medio bloque que cuelga.
Para estudiar el movimiento de las dos masas
deslizantes y del bloque que cuelga, nos situamos en el Sistema de Referencia no inercial que gira con la varilla con velocidad
angular ω. Consideremos el sistema formado por una masa deslizante situada a
una distancia r del eje de rotación y medio bloque que cuelga.
- El bloque que cuelga ejerce una fuerza Mg/2
- La fuerza centrífuga Fc=(m/2)ω2r.
Bajo la acción de estas fuerzas, las masas deslizantes experimentan una aceleración a=d2r/dt2 en la dirección radial, a lo largo de la varilla; el bloque se mueve verticalmente con la misma aceleración. La segunda ley de Newton se escribe
Resolvemos esta ecuación diferencial mediante procedimientos numéricos con las siguientes condiciones iniciales: en el instante t=0, la velocidad radial de la masa deslizante es dr/dt=0, y su distancia al eje r=r0.
Conocida la distancia r de las masas deslizantes al eje de rotación en el instante t, se calcula la velocidad angular ω de rotación sabiendo que el momento angular L permanece constante.
La posición de equilibrio re, cuando la fuerza neta sobre la masa deslizante es cero, es
Curvas de energía potencial
La energía inicial del sistema, cuando las masas se encuentran sujetas, es la suma de
- la energía cinética de las dos masas deslizantes que se mueven con velocidad tangencial ω0·r0.
- la energía potencial del bloque de masa M que está a una altura r0 sobre el origen.
Al cabo de un cierto tiempo t, las masas deslizantes distan r del eje de rotación, y la varilla gira con velocidad angular ω=dθ/dt. Cada una de las masas lleva una velocidad en la dirección radial vr=dr/dt y en la dirección tangencial vθ=r(dθ/dt). El bloque se mueve con velocidad vr=dr/dt. La energía total del sistema es
- El primer término, es la energía cinética del bloque
- El segundo término, es la energía cinética de las masas deslizantes
- El tercer término, es la energía potencial del bloque que cuelga
Teniendo en cuenta que el momento angular es constante, podemos escribir la energía E del sistema en función de r y de su derivada dr/dt,
Si dividimos la energía E entre las dos masas iguales, podemos considerar que cada una de ellas se mueve en un potencial efectivo
La fuerza resultante sobre cada una de las masas deslizantes y medio bloque se obtiene derivando la energía potencial y cambiando de signo.
que como vemos es la diferencia entre la fuerza centrífuga y la fuerza que ejerce el medio bloque que cuelga.
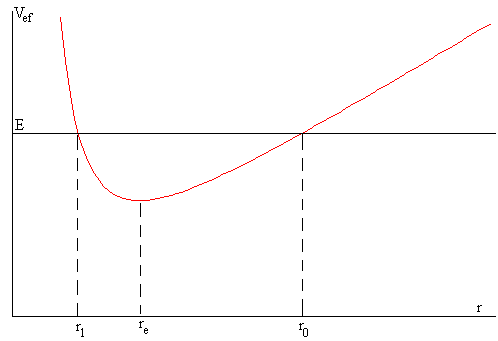
En la figura, vemos la representación gráfica de la energía potencial efectiva Vef(r) cuando las masas deslizantes salen de la posición inicial r0, con velocidad radial nula dr/dt=0. Si su energía total es E (recta horizontal), las masas llegan a la posición de retorno r1 al cabo de un cierto tiempo, cambian el sentido de la velocidad radial y regresan a la posición r0, oscilando con un determinado periodo.
La posición de retorno r1 se calcula resolviendo la ecuación Vef(r)=E
Como una de las raíces es r0, la ecuación cúbica se transforma en una ecuación de segundo grado
La raíz positiva de la ecuación de segundo grado es
Como vemos en la figura, la curva de la energía potencial efectiva presenta un mínimo, en la posición re. Este mínimo se obtiene igualando la derivada primera de Vef(r) a cero, es decir, cuando f(r)=-dVef(r)/dr=0
Ejemplo
-
Masa de las partículas deslizantes m/2=0.5 kg
-
Masa del bloque que cuelga M=0.5 kg
-
Velocidad angular inicial de rotación ω0=1.0 rad/s
-
Las masas deslizantes se liberan cuando su distancia al eje de rotación es r0=0.6 m
Momento angular
La energía del sistema es
Posición de equilibrio es
Posición de retorno dr/dt=0 de las masas deslizantes es
La velocidad angular ω1 de rotación cuando las masas deslizantes se encuentran en esta posición es
Las masas deslizantes oscilan entre las posiciones r0 y r1.
Actividades
Se introduce
-
La masa M del bloque que cuelga, en el control de edición titulado Masa bloque
-
La masa de las dos partículas deslizantes se ha fijado en m=1 kg, 0.5 kg cada una
-
La velocidad angular inicial de rotación se ha fijado en ω0=1 rad/s
-
La distancia r0 de las masas deslizantes al eje de rotación, actuando en la barra de desplazamiento titulada Distancia al eje
Se pulsa el botón titulado Nuevo
Se observa el sistema en el estado inicial. Las masas deslizantes fijadas a la distancia r0 del eje de rotación, el bloque a una altura r0 por encima del origen. La varilla y las masas deslizantes están girando con velocidad angular uniforme de ω0=1 rad/s.
Se pulsa el botón titulado Empieza
Se liberan las masas deslizantes y se observa su movimiento a lo largo de la varilla y del bloque hacia arriba y hacia abajo. Se dibujan las fuerzas sobre una masa deslizante:
-
La fuerza centrífuga, en color rojo
-
La mitad del peso del bloque que cuelga, en color azul.
El programa interactivo resuelve la ecuación diferencial del movimiento de las masas deslizantes a lo largo de la dirección radial por el procedimiento de Runge-Kutta. Verifica que se cumple el principio de conservación de la energía, comparando la energía inicial del sistema E0 y la energía E del sistema en el instante t.
Se denomina error relativo al cociente
Si esta cantidad es mayor que el 1% ó 0.01 el programa interactivo se detiene, e invita al usuario a disminuir la masa del bloque.
Si se activa la casilla titulada Gráfica, podemos ver la curva de la energía potencial efectiva de una masa deslizante, Vef(r) en función de la distancia r al eje de rotación. Para una energía total E de la masa deslizante (línea horizontal de color negro), se muestra:
-
la energía potencial, un segmento vertical de color rojo
-
la energía cinética correspondiente al movimiento en la dirección radial, un segmento de color azul.
En las posiciones extremas de retorno, la velocidad radial es cero.
En el mínimo, la masa deslizante está en equilibrio.
Referencias
Telfair D., Brooks J. T., Motion subject to a central force. An apparatus for demostrating orbital stability. Am. J. Phys. 30 (1962) pp.561-564
