Movimiento curvilíneo
Supongamos que el movimiento tiene lugar en el plano XY. Situamos un origen y unos ejes y representamos la trayectoria del móvil, es decir, el conjunto de puntos por los que pasa el móvil. Las magnitudes que describen un movimiento curvilíneo son:
Vector posición.
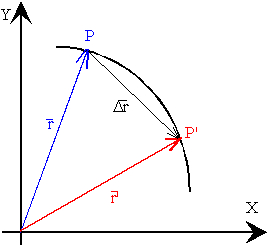 Como la posición del móvil cambia con el tiempo. En el instante t, el móvil se encuentra en el punto P, o en otras palabras, su vector posición es r y en el instante t' se encuentra en el punto P', su posición viene dada por el
vector r'.
Como la posición del móvil cambia con el tiempo. En el instante t, el móvil se encuentra en el punto P, o en otras palabras, su vector posición es r y en el instante t' se encuentra en el punto P', su posición viene dada por el
vector r'.
Diremos que el móvil se ha desplazado Δr=r’-r en el intervalo de tiempo Δt=t'-t. Dicho vector tiene la dirección de la secante que une los puntos P y P'.
Vector velocidad
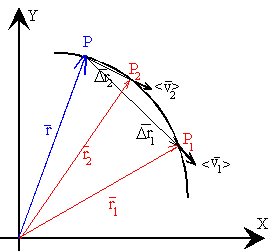 El vector velocidad media, se define como el cociente entre el vector
desplazamiento Δr y el tiempo que ha empleado en
desplazarse Δt.
El vector velocidad media, se define como el cociente entre el vector
desplazamiento Δr y el tiempo que ha empleado en
desplazarse Δt.
El vector velocidad media tiene la misma dirección que el vector desplazamiento, la secante que une los puntos P y P1 cuando se calcula la velocidad media <v1> entre los instantes t y t1.
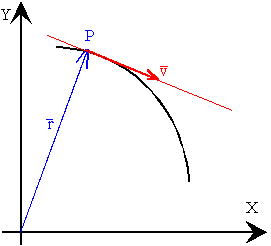 El vector velocidad en un instante, es el límite del vector velocidad
media cuando el intervalo de tiempo tiende a cero.
El vector velocidad en un instante, es el límite del vector velocidad
media cuando el intervalo de tiempo tiende a cero.
Como podemos ver en la figura, a medida que hacemos tender el intervalo de tiempo a cero, la dirección del vector velocidad media, la recta secante que une sucesivamente los puntos P, con los puntos P1, P2....., tiende hacia la tangente a la trayectoria en el punto P.
En el instante t, el móvil se encuentra en P y tiene una velocidad v cuya dirección es tangente a la trayectoria en dicho punto.
Vector aceleración
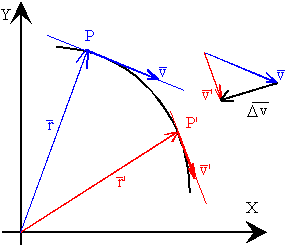 En el instante t el móvil se encuentra en P y tiene una velocidad v cuya dirección es tangente a la trayectoria en dicho punto.
En el instante t el móvil se encuentra en P y tiene una velocidad v cuya dirección es tangente a la trayectoria en dicho punto.
En el instante t' el móvil se encuentra en el punto P' y tiene una velocidad v'.
El móvil ha cambiado, en general, su velocidad tanto en módulo como en dirección, en la cantidad dada por el vector diferencia Δv=v’-v.
Se define la aceleración media como el cociente entre el vector cambio de velocidad Δv y el intervalo de tiempo Δt=t'-t, en el que tiene lugar dicho cambio.
Y la aceleración a en un instante
Resumiendo, las ecuaciones del movimiento curvilíneo en el plano XY son
La primera fila corresponde, a las ecuaciones de un movimiento rectilíneo a lo largo del eje X, la segunda fila corresponde, a las ecuaciones de un movimiento rectilíneo a lo largo del eje Y, y lo mismo podemos decir respecto del eje Z.
Por tanto, podemos considerar un movimiento curvilíneo como la composición de movimientos rectilíneos a lo largo de los ejes coordenados.
Ejemplo 1:
Un automóvil describe una curva plana tal que sus coordenadas rectangulares, en función del tiempo están dadas por las expresiones: x=2t3-3t2, y=t2-2t+1 m. Calcular:
- Las componentes de la velocidad en cualquier instante.
vx=dx/dt=6t2-6t m/s
vy=dy/dt=2t-2 m/s
- Las componentes de la aceleración en cualquier instante.
ax=dvx/dt=12t-6 m/s2
ay=dvy/dt=2 m/s2
Ejemplo 2:
Un punto se mueve en el plano de tal forma que las componentes rectangulares de la velocidad en función del tiempo vienen dadas por las expresiones: vx=4t3+4t, vy=4t m/s. Si en el instante inicial t0=0 s, el móvil se encontraba en la posición x0=1, y0=2 m. Calcular:
- Las componentes de la aceleración en cualquier instante
- Las coordenadas x e y, del móvil, en función del tiempo.
Dada la velocidad vx=4t3+4t del móvil, el desplazamiento x-1 entre los instantes 0 y t se calcula mediante la integral
Dada la velocidad vy=4t del móvil, el desplazamiento y-2 entre los instantes 0 y t se calcula mediante la integral
Ejemplo 3:
Se lanza una pelota verticalmente hacia arriba con una velocidad de 20 m/s desde la azotea de un edificio de 50 m de altura. La pelota además es empujada por el viento, produciendo un movimiento horizontal con una aceleración de 2 m/s2Calcular:
- La distancia horizontal entre el punto de lanzamiento y de impacto
- La altura máxima
- Los
instantes y los valores de las componentes de la velocidad cuando la pelota
se encuentra a 60 m de altura sobre el suelo.
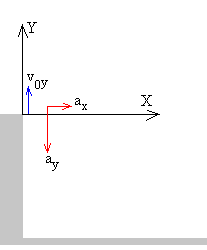
-
Primero, se establece el origen en el punto del lanzamiento y los ejes X e Y apuntando hacia arriba.
-
Se determinan los signos de las velocidades iniciales v0x=0 y v0y=20 y de la aceleración ay=-10.
- Se escriben las ecuaciones del movimiento:
- Movimiento uniformemente acelerado a lo largo del eje X
ax=2
vx=2t
x=2t2/2
- Movimiento uniformemente acelerado a lo largo del eje Y
(movimiento de caída de los cuerpos)
ay=-10
vy=20+(-10)t
y=20t+(-10)t2/2
- El
punto de impacto tiene de coordenadas x desconocida e y=-50
m. Dado y se obtiene el valor de t y luego el valor de x.
y=-50 m
t=1.74 s
x=3.03 m
- La altura máxima se obtiene cuando la velocidad vertical es
cero
vy=0 m/s
t=2 s
y=20 m
La altura desde el suelo es 20+50=70 m.
- El móvil se encuentra en dos instantes a 60 m de altura sobre
el suelo (10 sobre el origen), ya que su trayectoria corta en dos puntos a
la recta horizontal y=10 m. La ecuación de segundo grado tiene dos raíces
10=20t+(-10)t2/2
t1=0.59 s y t2=3.41 s.
