Torpedo a la caza de un submarino

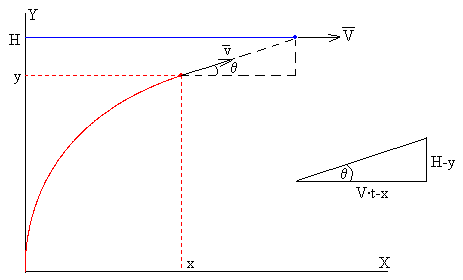
En esta página, se describe la trayectoria que sigue un torpedo disparado desde el origen cuando persigue a un submarino que se mueve con velocidad constante V a lo largo de la trayectoria rectilínea y=H. El torpedo se mueve con velocidad constante v, pero su dirección apunta siempre hacia el submarino, tal como se muestra en la figura.

Ecuación del movimiento del torpedo

En el triángulo rectángulo de la figura, la base es la diferencia entre el desplazamiento del submarino V·t y la del torpedo x. La altura es la diferencia H-y. Como la dirección de la velocidad del torpedo es la línea recta que pasa por la posición del torpedo y la del submarino en el instante t, tendremos que

$\tan θ = \frac{v_{y}}{v_{x}} = \frac{H - y}{V \cdot t - x} v = \sqrt{v_{x}^{2} + v_{y}^{2}}$

o de forma alternativa

$V \cdot t - x = (H - y) \frac{v_{x}}{v_{y}}$

Diferenciando ambos miembros con respecto del tiempo

$\begin{array}{l} V - v_{x} = - v_{y} \frac{v_{x}}{v_{y}} + (H - y) \frac{d}{d t} (\frac{v_{x}}{v_{y}}) \frac{V}{H - y} = \frac{d}{d t} \sqrt{\frac{v^{2}}{v_{y}^{2}} - 1} \\ \frac{V}{H - y} = \frac{- v^{2}}{v_{y}^{2} \sqrt{v^{2} - v_{y}^{2}}} \frac{d v_{y}}{d t} \end{array}$

Teniendo en cuenta que

$\begin{array}{l} \frac{d v_{y}}{d t} = \frac{d y}{d t} \frac{d v_{y}}{d y} = v_{y} \frac{d v_{y}}{d y} \\ \frac{V}{H - y} d y = \frac{- v^{2}}{v_{y} \sqrt{v^{2} - v_{y}^{2}}} d v_{y} \end{array}$

Integramos ambos miembros, sabiendo que el torpedo parte del origen y=0, y su velocidad inicial es v_y=v, dirigida a lo largo del eje Y.

$\int_{0}^{y} \frac{V}{H - y} d y = - v^{2} \int_{v}^{v_{y}} \frac{d v_{y}}{v_{y} \sqrt{v^{2} - v_{y}^{2}}}$

Para resolver la integral de la derecha, se hace el cambio de variable z=1/v_y

$\int \frac{- d z}{\sqrt{v^{2} z^{2} - 1}} = - \frac{1}{v} \ln | v z + \sqrt{v^{2} z^{2} - 1} | + c$

Deshaciendo el cambio de variable y evaluando ambas integrales en los límites inferior y superior, se obtiene.

$\begin{array}{l} - \frac{V}{v} \ln (\frac{H - y}{H}) = \ln (\frac{v + \sqrt{v^{2} - v_{y}^{2}}}{v_{y}}) \\ v_{y} {(1 - \frac{y}{H})}^{- V / v} - v = \sqrt{v^{2} - v_{y}^{2}} \end{array}$

Elevando ambos miembros al cuadrado y despejando v_y

$v_{y} = \frac{2 v}{{(1 - \frac{y}{H})}^{V / v} + {(1 - \frac{y}{H})}^{- V / v}}$

Resolvemos la ecuación diferencial de primer orden

$\frac{d y}{d t} - \frac{2 v}{{(1 - \frac{y}{H})}^{V / v} + {(1 - \frac{y}{H})}^{- V / v}} = 0$

con las condiciones iniciales siguientes: en el instante t=0, el torpedo parte del origen, y=0.

Alternativamente, integramos de nuevo para obtener la ordenada y del torpedo en función del tiempo t.

Para ello, hacemos el cambio de variable z=1-y/H.

$\begin{array}{l} - H \int_{1}^{z} (z^{V / v} + z^{- V / v}) d z = \int_{0}^{t} 2 v \cdot d t \\ t = - \frac{H}{2} {\frac{z^{V / v + 1}}{V + v} + \frac{z^{- V / v + 1}}{- V + v} - \frac{2 v}{- V^{2} + v^{2}}} \end{array}$

Esta es una ecuación implícita de la ordenada y en función del tiempo t.

Una vez obtenida la ordenada y en función del tiempo t, se calcula la abscisa x, mediante la relación deducida al principio de esta página.

$\begin{array}{l} V \cdot t - x = (H - y) \frac{v_{x}}{v_{y}} \\ x = V \cdot t - H z \frac{v_{x}}{v_{y}} \\ v_{y} = \frac{2 v}{z^{V / v} + z^{- V / v}} v_{x} = \sqrt{v^{2} - v_{y}^{2}} = v \frac{1 - z^{2 V / v}}{1 + z^{2 V / v}} \end{array}$

Sustituimos el tiempo t y obtenemos la ecuación de la trayectoria

$\frac{x}{H} = \frac{1}{2} \cdot \frac{z^{1 + V / v}}{1 + V / v} - \frac{1}{2} \cdot \frac{z^{1 - V / v}}{1 - V / v} + \frac{V / v}{1 - V^{2} / v^{2}}$

Distintos casos

Cuando la velocidad del torpedo es mayor que la del submarino, v>V.

Cuando y=H ó z=0 se produce el impacto del torpedo y la posible destrucción del submarino.

La posición del punto de impacto es

$x = H \frac{V / v}{1 - V^{2} / v^{2}}$

que es positivo solamente si v>V. La velocidad v del torpedo tiene que ser necesariamente mayor que la velocidad V del submarino para que haya impacto.

El instante t en el que se produce es

$t = H \frac{v}{v^{2} - V^{2}}$

Cuando la velocidad del torpedo es menor que la del submarino, v<V.

El torpedo y el submarino se aproximan hasta una distancia mínima y luego se alejan.

$L = \sqrt{{(V \cdot t - x)}^{2} + {(H - y)}^{2}} = (H - y) \frac{v}{v_{y}} = H z \frac{v}{v_{y}} = \frac{H}{2} (z^{1 - V / v} + z^{1 - V / v})$

El mínimo se obtiene derivando L respecto de z e igualando a cero.

$(1 - \frac{V}{v}) z^{- V / v} + (1 + \frac{V}{v}) z^{V / v} = 0$

Haciendo algunas operaciones obtenemos

$L_{\min} = \frac{H}{\sqrt{1 - v^{2} / V^{2}}} {(\frac{V - v}{V + v})}^{v / (2 V)}$

Cuando la velocidad del submarino y del torpedo es la misma, V=v.

La componente Y de la velocidad del torpedo vale

$\frac{d y}{d t} = \frac{2 v}{(1 - \frac{y}{H}) + {(1 - \frac{y}{H})}^{- 1}}$

Hacemos el cambio de variable z=1-y/H para integrar

$\begin{array}{l} - H \int_{1}^{z} (z + \frac{1}{z}) d z = \int_{0}^{t} 2 v \cdot d t \\ t = \frac{H}{4 v} (1 - z^{2} - 2 \ln z) \end{array}$

La ecuación de la trayectoria es

$\frac{x}{H} = \frac{z^{2} - 1}{4} - \frac{1}{2} \ln z$

Cuando v→V, la distancia entre el submarino L_min y el torpedo tiende a H/2, como puede comprobarse fácilmente

Ejemplo.

Cuando la velocidad v del torpedo es menor que la del submarino V=1. Por ejemplo, v=0.8.

La distancia de máximo acercamiento es

$L_{\min} = \frac{1.0}{\sqrt{1 - {0.8}^{2}}} {(\frac{1 - 0.8}{1 + 0.8})}^{0.8 / 2} = 0.692$

En la posición

$\begin{array}{l} (1 - \frac{V}{v}) z^{- V / v} + (1 + \frac{V}{v}) z^{V / v} = 0 \\ - 0.25 \cdot z^{- 1.25} + 2.25 \cdot z^{1.25} = 0 \end{array}$

z=0.415, y=0.585

En el instante

$\begin{array}{l} t = - \frac{H}{2} {\frac{z^{V / v + 1}}{V + v} + \frac{z^{- V / v + 1}}{- V + v} - \frac{2 v}{- V^{2} + v^{2}}} \\ t = - \frac{1}{2} {\frac{{0.415}^{}}{1.8} + \frac{{0.415}^{- 0.25}}{- 0.2} - \frac{2 \cdot 0.8}{- 1^{2} + {0.8}^{2}}} = 0.854 \end{array}$

La abscisa x se obtiene a partir de la ecuación de la trayectoria

$\begin{array}{l} \frac{x}{H} = \frac{1}{2} \cdot \frac{z^{1 + V / v}}{1 + V / v} - \frac{1}{2} \cdot \frac{z^{1 - V / v}}{1 - V / v} + \frac{V / v}{1 - V^{2} / v^{2}} \\ x = \frac{1}{2} \frac{{0.415}^{2.25}}{2.25} - \frac{1}{2} \frac{{0.415}^{- 0.25}}{- 0.25} + \frac{1.25}{1 - {1.25}^{2}} = 0.300 \end{array}$

Cuando la velocidad v del torpedo es mayor que la del submarino V=1. Por ejemplo, v=2.

La posición del punto de impacto es

$\begin{array}{l} x = H \frac{V / v}{1 - V^{2} / v^{2}} \\ x = 1 \cdot \frac{0.5}{1 - {0.5}^{2}} = \frac{2}{3} \end{array}$

en el instante

$\begin{array}{l} t = H \frac{v}{v^{2} - V^{2}} \\ t = 1 \cdot \frac{2}{2^{2} - 1^{2}} = \frac{2}{3} \end{array}$

Actividades

Se introduce

La velocidad v del torpedo, actuando en la barra de desplazamiento titulada V. torpedo.
La velocidad V del submarino se ha fijado en V=1
La distancia inicial H entre el torpedo y el submarino se ha fijado en H=1.

Se pulsa el botón titulado Empieza.

Se observa la trayectoria curvilínea del torpedo (en color rojo) y la rectilínea del submarino (en color azul).

La flecha de color negro, representa la velocidad del torpedo, su dirección es tangente a la trayectoria que es a su vez, la recta que une el torpedo y el submarino.

El programa interactivo resuelve numéricamente la ecuación diferencial de primer orden que proporciona el valor de la ordenada y en función del tiempo t, y luego calcula la abscisa x, mediante la relación geométrica establecida al principio de esta página.

CinemaApplet5 aparecerá en un explorador compatible con JDK 1.1.

Referencias

Mungan C. E., A classic chase problem solved from a physics perspective. Eur. J. Phys. 26 (2005), pp. 985-990