Barreras de potencial
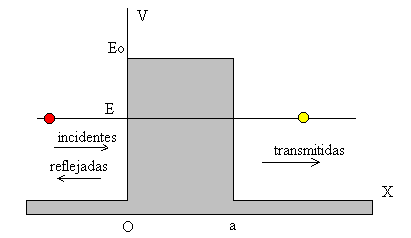
El hecho de que la función de onda pueda extenderse más allá de los límites clásicos del movimiento da lugar a un importante fenómeno llamado penetración de la barrera de potencial. Consideremos el potencial representado en la figura que consta de dos escalones y que se denomina barrera de potencial de altura E0 y anchura a.
El caso más interesante se da, cuando la energía de las partículas sea menor que la de la barrera. La Mecánica Clásica requiere que una partícula proveniente de la izquierda con E<E0 se refleje en el origen x=0, ya que en la región (0, a) la energía cinética de la partícula es negativa.
Las partículas que hayan penetrado una distancia mayor o igual que a, tendrían una energía cinética igual a su energía total (la energía potencial vuelve a ser cero) y por tanto, se moverán hacia la derecha con igual velocidad que las incidentes. Estas partículas que han atravesado la barrera se denominan transmitidas y han pasado de la primera a la tercera región de potencial a través de la región intermedia, clásicamente prohibida (la energía cinética de la partícula es negativa).
Una barrera de potencial
Discutiremos ahora el problema desde el punto de vista de la Mecánica Cuántica, resolviendo la ecuación de Schrödinger en las tres regiones y aplicando las condiciones de continuidad de la función de onda y de su derivada primera en los puntos x=0, y x=a.
Resolveremos primero, el caso en el que la energía de las partículas E es menor que la del escalón E0, el caso más interesante desde el punto de vista físico. Posteriormente, estudiamos el caso en el que la energía de la partícula E es mayor que la del escalón E0.
E<E0.
- Región x<0
- Región 0<x<a, aquí E<E0
- Región x>a
La función de onda Ψ1(x) contiene las partículas incidentes y reflejadas, Ψ2(x) decrece exponencialmente, la exponencial positiva no está excluida ya que la región clásicamente prohibida no es indefinida como en el caso del escalón de potencial. Debido a que Ψ2(x) no ha alcanzado el valor cero en x=a, la función de onda continúa a la derecha de dicho punto, con amplitud A'. La función de onda Ψ3(x) representa las partículas transmitidas.
Desde el punto de vista de la Mecánica Cuántica, es posible que una partícula atraviese la barrera de potencial aún cuando su energía cinética sea menor que la altura de la barrera.
Aplicamos las condiciones de continuidad de la función de onda y de su derivada primera en los puntos x=0
Aplicamos las condiciones de continuidad de la función de onda y de su derivada primera en los puntos x=a,
Se denomina coeficiente de transmisión a la proporción de partículas incidentes que son transmitidas
El coeficiente de transmisión disminuye rápidamente a medida que se incrementa la anchura de la barrera de potencial.
E>E0
Para E<E0, T es menor que la unidad. Sin embargo, para E>E0, T alcanza el valor máximo, para valores concretos del cociente E/E0.
Resolviendo de nuevo, la ecuación de Schrödinger en las tres regiones
- Región x<0
- Región 0<x<a, ahora E>E0.
- Región x>a
Las ecuaciones de continuidad de la función de onda y de su derivada primera en x=a, relacionan C y D con A', y en x=0, relacionan A y B con C y D, y por tanto, con A'
Finalmente, obtenemos la siguiente expresión para el coeficiente de transmisión
Como podemos apreciar T toma el valor máximo 1, cuando k'a=nπ, siendo n un número entero. Como k' es el número de onda, k'=2π/λ', se obtiene que
que relaciona la longitud de onda λ' de la partícula en la barrera de potencial con la anchura a de la misma, para que se obtenga el máximo en el coeficiente de transmisión. Los valores de la energía E, o mejor del cociente E/E0 ,para los cuales hay un máximo del coeficiente de transmisión se denominan resonancias.
N barreras de potencial
Estudiaremos ahora el caso en el que hay N barreras de potencial de la misma anchura a y separadas unas de otras la misma cantidad b tal como se aprecia en la figura. Observaremos que se producen picos de resonancia adicionales, dando lugar a un comportamiento complejo del coeficiente de transmisión.
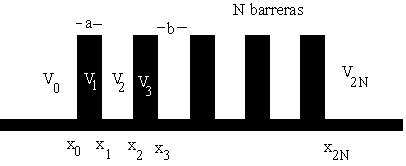
Resolvemos la ecuación de Schrödinger para cada una de las distintas regiones
Donde qj es un número complejo real o imaginario dependiendo de que E>Vj o E<Vj.
En las fronteras entre las regiones, aplicamos las condiciones de continuidad. Sea la frontera entre las regiones j-1 y j, cuya abscisa es xj.
que relaciona los coeficientes Aj y Bj con Aj-1 y Bj-1
Teniendo en cuenta que solamente hay partículas trasmitidas en la región 2N, resulta que B2N=0. Obtenemos los valores de todos los coeficientes Aj y Bj en términos de A2N que actúa como factor de escala.
El coeficiente de transmisión se define como la proporción de partículas incidentes que se trasmiten y se obtiene mediante el cociente.
Funciones de onda
El primer programa interactivo, tiene por objeto mostrar las funciones de onda en las distintas regiones de un sistema de barreras de potencial, para una energía E, y calcular el coeficiente de transmisión para dicho valor de la energía.
Se define el sistema de barreras de potencial, introduciendo
- el número de barreras, en el control de edición titulado nº de barreras
- la anchura de cada barrera, en el control de edición titulado Anchura de la barrera
- la separación entre los mismas, en el control de edición titulado Separación entre barreras
- la altura de la barrera de potencial se ha fijado en 5 unidades.
- el valor de la energía en el control de edición titulado Energía
Se pulsa en el botón Función, y se muestra la representación gráfica de la función de onda en las distintas regiones:
- En color azul, la función de onda correspondiente a todas las regiones de potencial, excepto la última, y representa a las partículas incidentes y reflejadas. Dicha función de onda aparece desdoblada en la primera región, en color azul claro la correspondiente a las partículas incidentes, y en color rosa la correspondiente a las partículas reflejadas.
- En la última región de potencial, se muestra en color rojo la función de onda correspondiente a las partículas trasmitidas
Se observará que hay continuidad al pasar de la función de onda de color azul (incidentes más reflejadas) a la de color rojo (transmitidas).
En la parte superior derecha de la ventana, se muestra el coeficiente de transmisión para el valor de la energía introducida.
Coeficiente de transmisión
El segundo programa interactivo, tiene por objeto mostrar el comportamiento del coeficiente de transmisión, representando dicho coeficiente en un amplio rango de energías.
Se define el sistema de barreras de potencial, introduciendo
- el número de barreras, en el control de edición titulado nº de barreras
- la anchura de cada barrera, en el control de edición titulado Anchura de la barrera
- la separación entre los mismas, en el control de edición titulado Separación entre barreras
- la altura de la barrera de potencial se ha fijado en 5 unidades.
Se pulsa en el botón titulado Potencial, y se muestra el sistema de barreras de potencial.
Se pulsa a continuación, en el botón titulado Transmisión, para que se represente el coeficiente de transmisión en el intervalo de 0 a 35 unidades de energía.
Dado que la representación gráfica puede llegar a ser compleja, mostrándose muchos picos (resonancias) juntos, podemos examinarla con más detalle el comportamiento del coeficiente de transmisión en un intervalo dado.
Se introduce
- el intervalo de energías, en los controles de edición titulados Intervalo,
Se pulsa en el botón titulado Transmisión. El mínimo intervalo que se representa es de 5 unidades de energía, o un múltiplo de dicha cantidad.
