Choque elástico de una partícula y una cuña

Se coloca una cuña de masa M y ángulo θ sobre un plano horizontal sin rozamiento. Una partícula de masa m y velocidad u golpea a la cuña.
Supondremos que el choque entre la partícula y la cuña es elástico y que su velocidad u es horizontal justamente antes del impacto.

Vamos a calcular la velocidad de la cuña y de la partícula después del choque, y su movimiento posterior.

Descripción

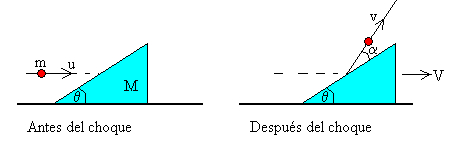
La partícula rebota en el plano inclinado haciendo la dirección de su velocidad v un ángulo θ+α con la horizontal tal como se indica en la figura. Después del choque, la cuña se mueve sobre el plano horizontal con velocidad constante V.
Para determinar v, V y α precisamos de tres ecuaciones

Conservación del momento lineal a lo largo de la dirección horizontal

mu=MV+mvcos(α+θ)

En un choque elástico la energía cinética de las partículas antes del choque es igual a la energía cinética de las partículas después del choque

1 2 m u 2 = 1 2 m v 2 + 1 2 M V 2

Durante la colisión, la fuerza N que ejerce la cuña sobre la partícula es normal al plano inclinado, y por tanto, la componente de la velocidad de la partícula paralela al plano inclinado permanece constante.

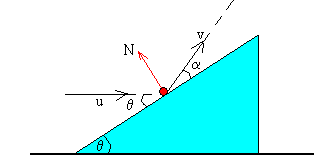
ucosθ=vcosα

Escribimos las tres ecuaciones en la forma equivalente

u=vcos⁡(α+θ)+qV q= M m u 2 = v 2 +q V 2 ucos⁡θ=vcos⁡α

Despejamos V y v de la primera y tercera ecuación y la sustituimos en la segunda

u 2 = u 2 cos 2 θ cos⁡ 2 α + u 2 q ( 1− cos⁡θcos⁡(α+θ) cos⁡α ) 2 cos 2 α= cos 2 θ+ 1 q ( cos⁡α−cos⁡θcos⁡(α+θ) ) 2 ( 1 q ( cos 4 θ+ cos 2 θ−2cos⁡θ )−1 ) cos 2 α+ 1 q sin⁡θ(1−cos⁡θ)sin⁡(2α)+ cos 2 θ+ 1 q sin 2 θ=0 acos⁡(2α)+bsin⁡(2α)+c=0 a= 1 2 ( 1 q ( 1+2 cos⁡ 4 θ−3 cos⁡ 2 θ )−1 ) b= 1 q sin 3 θcos⁡θ c= 1 2q sin 2 θ− 1 2 + cos 2 θ

Para obtener estas expresiones se han empleado las relaciones trigonométricas

cos⁡(α+θ)=cos⁡αcos⁡θ−sin⁡αsin⁡θ cos 2 α= 1+cos⁡(2α) 2 sin 2 θ+ cos 2 θ=1

Escribimos la ecuación

acos(2α)+c=-bsin(2α)

Elevamos al cuadrado y obtenemos una ecuación de segundo grado en cos(2α). Una de las raíces (+) es la solución, la otra (-) nos proporciona los datos de partida.

( a 2 + b 2 ) cos 2 (2α)+2accos⁡(2α)− b 2 + c 2 =0 cos⁡(2α)= −2ac+ 4 a 2 c 2 −4( c 2 − b 2 )( a 2 + b 2 ) 2( a 2 + b 2 ) cos⁡(2α)= −ac+b a 2 + b 2 − c 2 a 2 + b 2

Una vez calculado el ángulo de desviación α de la partícula respecto del plano inclinado, se calcula la velocidad v de la partícula y la velocidad V de la cuña después del choque

v=u cos⁡θ cos⁡α V= u q ( 1− cos⁡θ cos⁡α cos⁡(α+θ) )

Después del choque

La cuña se mueve a lo largo del plano horizontal con velocidad constante V.
La partícula describe un movimiento bajo la aceleración constante de la gravedad. Situamos el origen en el punto de impacto sobre la cuña. Las ecuaciones del movimiento son

x=vcos⁡(α+θ)t y=vsin⁡(α+θ)t− 1 2 g t 2

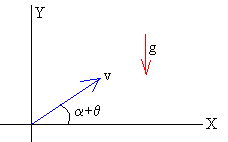
Caso particular

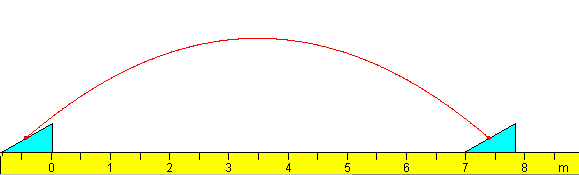
Cuando la velocidad de la cuña V es igual a la componente horizontal de la velocidad de la partícula v·cos(α+θ). La partícula regresa al punto de impacto, tal como se aprecia en la figura.

Para que esto suceda el ángulo θ del plano inclinado ha de estar relacionado con las masas de la partícula y la cuña q=M/m

Si V= v·cos(α+θ).

De la conservación del momento lineal
u=(1+q) v·cos(α+θ).

De la constancia de la energía cinética
u²=v²+qv²cos²(α+θ).

Elevamos al cuadrado la primera ecuación y la combinamos con la segunda, obteniendo

1+q+ q 2 = 1 cos⁡ 2 (α+θ) q+ q 2 = tan 2 (α+θ)= ( tan⁡α+tan⁡θ 1−tan⁡αtan⁡θ ) 2

Combinamos la conservación del momento lineal
u=(1+q) v·cos(α+θ).

Con la constancia de la componente de la velocidad de la partícula a lo largo del plano inclinado (la fuerza que ejerce la cuña sobre la partícula es perpendicular al plano inclinado)
ucosθ=vcosα

1 cos⁡θ =(1+q) cos⁡(α+θ) cos⁡α tan⁡α= (1+q)cos⁡θ− 1 cos⁡θ (1+q)sin⁡θ = qcot⁡θ−tan⁡θ (1+q)

sustituyendo la expresión de tanα. Llegamos a la relación

q 2 +q= ( 1 q+1 ( q tan⁡θ −tan⁡θ )+tan⁡θ 1− 1 q+1 ( q tan⁡θ −tan⁡θ )tan⁡θ ) 2 tan⁡θ= q q+1

Ejemplo

q= 1 2 tan⁡θ= 3 θ=30º

Actividades

Se introduce

El cociente entre las masas de la cuña y de la partícula q=M/m, en el control de edición titulado Masa/cuña/partícula
El ángulo del plano inclinado θ, actuando en la barra de desplazamiento titulada Ángulo

Se pulsa el botón titulado Nuevo

Se ha fijado la velocidad de la partícula inmediatamente antes del choque en u=1.0 m/s, su dirección es horizontal

Se pulsa el botón titulado Empieza

Se observa el movimiento de la cuña y de la partícula después del choque.

En la parte superior del applet se muestra los datos de:

La velocidad V de la cuña después del choque
La velocidad v de la partícula inmeditamente después del choque
El ángulo α que forma la dirección de dicha velocidad con el plano inclinado

stokesApplet aparecerá en un explorador compatible con JDK 1.1.

Referencias

Physics challenge for teachers and students. Solutions to November 2006 challenge. The Physics Teacher, Vol 45, 2007