• Inicio
• Dinámica
• Sistemas de partículas
• Choques

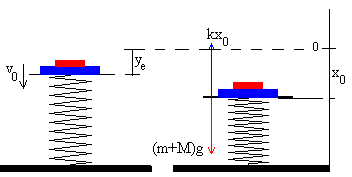
Choque inelástico entre un bloque que cae y una plataforma que descansa sobre un muelle elástico.

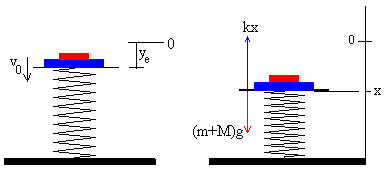
Un bloque de masa m, está situado a una altura h sobre el origen O, cae sobre una plataforma de masa M cuyo soporte es un muelle de constante k. El choque es inelástico, el bloque queda pegado a la plataforma. Determinar el movimiento del sistema formado por el bloque, la plataforma y el muelle.

Ecuación del movimiento

1. Posición de equilibrio de la plataforma M sobre el muelle de constante k.

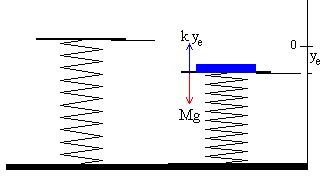La posición de equilibrio ye es aquella en la que el peso del la plataforma se equilibra con la fuerza que ejerce el muelle k·ye =Mg

2. El bloque de masa m cae desde una altura h+y_e antes de chocar con la plataforma.

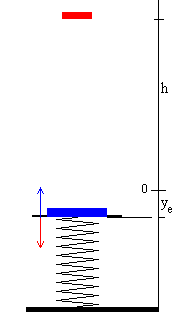La velocidad antes del choque es ${\displaystyle v_1=\sqrt{2g\left(h+y_e\right)}}$ Conservación del momento lineal En el instante del choque, supondremos que el bloque y la plataforma forman un sistema aislado. Aplicando el principio de conservación del momento lineal mv0=(m+M)v1.

4. Posición de equilibrio del sistema formado por el muelle, la plataforma y el bloque.

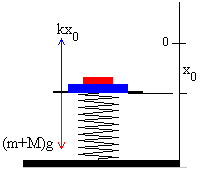La posición de equilibrio x0 es aquella en la que el peso del la plataforma y el bloque se equilibra con la fuerza que ejerce el muelle k·x0=(M+m)g

5. Sistema oscilante.

El periodo P del  Movimiento Armónico Simple es

${\displaystyle P=2\pi \sqrt{\frac{M+m}{k}}}$

La frecuencia angular es ω =2π /P

La ecuación del MAS es

x=-x₀+A·sin(ω t+φ )

La velocidad del sistema bloque-plataforma se obtiene derivando la x respecto del tiempo

v=Aω ·cos(ω t+φ )

La amplitud A y la fase inicial φ , se determina a partir de las condiciones iniciales.

Como podemos ver en la figura, el sistema parte en el instante t=0 de la posición -y_e con velocidad v₀ que tiene el sistema bloque- plataforma después del choque.

Tenemos el sistema de dos ecuaciones con dos incógnitas

-y_e =-x₀+A·sinφ
-v₀=Aω ·cosφ

A partir de las cuales, obtenemos la amplitud A y la fase inicial φ .

Ejemplo

Sea un sistema formado por

• Un bloque de masa m=10 kg
• Una plataforma de masa M=20 kg
• Un muelle de constante elástica k=2000 N/m

El bloque se deja caer desde una altura de 1 m sobre el nivel del muelle sin deformar, que tomamos como origen.

1. Posición de equilibrio de la plataforma M sobre el muelle de constante k.

20·9.8=2000·y_e por lo que y_e=9.8 cm

2. La velocidad antes del choque del bloque

El bloque cae desde una altura de 1.098 m, su velocidad es

v₁=4.64 m/s

3. Choque del bloque contra la plataforma

10·4.64=(10+20)·v₀ por lo que v₀=1.546 m/s ó 154.6 cm/s

4. Posición de equilibrio del sistema formado por el bloque, la plataforma y el muelle

(20+10)·9.8=2000·x₀, por lo que x₀=14.7 cm

5. Movimiento Armónico Simple

Periodo de la oscilación

${\displaystyle P=2\pi \sqrt{\frac{(20+10)}{2000}}=0.93\text{s}}$

La frecuencia angular ω =8.16 rad/s

Ecuación del MAS

x=-14.7+A·sin(ω t+φ ) cm
v= Aω ·cos(ω t+φ ) cm/s

Condiciones iniciales, en el instante t=0

-9.8=-14.7+A·sinφ
-154.6=Aω · cosφ

φ =165.5º=2.89 rad
A=19.56 cm

La ecuación del MAS es

x=-14.7+19.56·sin(8.16t+2.89) cm

• La posición más baja del conjunto formado por el bloque y la plataforma se alcanza cuando 8.16t+2.89=3π/2, es decir en el instante t₂=0.22 s, y vale x₂=-34.26 cm
• La posición más alta del conjunto formado por el bloque y la plataforma se alcanza cuando 8.16t+2.89=3π/2+π, es decir en el instante t₃=0.61 s, y vale x₃=4.86 cm

La posición más baja se vuelva a alcanzar en los instantes t₂+nP,  siendo P el periodo de la oscilación y n un número entero positivo. La posición más alta se vuelva a alcanzar en los instantes t₃+nP.

Balance energético

1. Antes del choque

• El bloque de masa m está en reposo a una altura h=1 m

E_p=mgh

• La plataforma ha descendido y_e

E_p=-Mg·y_e

• El muelle está comprimido y_e

${\displaystyle E_{pe}=\frac{1}{2}k{y}_e^2}$

2. En el momento del choque

La energía potencial del bloque de masa m se ha transformado en energía cinética

${\displaystyle \frac{1}{2}m{v}_1^2=mg(h+y_e)}$

3. El choque es inelástico, una parte de la energía se pierde

${\displaystyle Q=\frac{1}{2}(m+M)v_0^2-\frac{1}{2}m{v}_1^2}$

donde v₀ es la velocidad del conjunto bloque-plataforma después del choque.

4. Después del choque la energía del sistema es

• Energía potencial del conjunto bloque–plataforma se encuentran a y_e por debajo del origen

E_p=-(M+m)g·y_e

• Energía cinética

${\displaystyle E_k=\frac{1}{2}(m+M)v_0^2}$

• Energía potencial elástica del muelle

${\displaystyle E_{pe}=\frac{1}{2}k{y}_e^2}$

En el ejemplo estudiado anteriormente

m=10 kg, M=20 kg, k=2000 N/m. La velocidad después del choque v₀=1.546 m/s

y la posición en la que ocurre el choque era y_e=0.098 m. La energía total

${\displaystyle E=-(20+10)·9.8·0.098+\frac{1}{2}(20+10)·{1.546}^2+\frac{1}{2}2000·{0.098}^2=16.64\text{J}}$

las posiciones x para las cuales v=0, se obtienen de la ecuación

${\displaystyle -(10+20)·9.8·x+\frac{1}{2}2000·x^2=16.64}$

Esta ecuación de segundo grado nos da dos posiciones x=0.3425 m y x=-0.048.

La posición más baja está 34.25 cm por debajo del origen, y la más alta 4.8 cm por encima del origen. Valores que obtuvimos en el apartado anterior.

5. La suma de estas tres clases de energías se va a mantener constante, mientras el sistema está oscilando, ya que el conjunto bloque-plataforma- muelle esta bajo la acción de dos fuerzas conservativas, el peso y la fuerza que ejerce el muelle deformado.

La ecuación diferencial del movimiento

Las fuerzas sobre el bloque y la plataforma son el peso y la fuerza que ejerce el muelle. La segunda ley de Newton se escribe

ma=-kx-mg

(como x≤0, –kx≥0 es positiva, tal como se muestra en la figura)

En forma de ecuación diferencial

${\displaystyle \frac{d^{2}x}{d{t}^2}+\frac{k}{m}x=-g{\omega }^2=\frac{k}{m}}$

La solución de esta ecuación diferencial es la suma de la solución de la ecuación diferencial homogénea

x₁=Asin(ωt)+Bcos(ωt) 

donde A y B son constantes que se determinan a partir de las condiciones iniciales

y de la solución particular

x₂=C

introduciendo la solución particular en la ecuación diferencial determinamos el valor de la constante C.

ω²C=-g

La solución de la ecuación diferencial completa es x=x₁+x₂

${\displaystyle \begin{array}{l}x=-\frac{g}{{\omega }^2}+A\sin (\omega t)+B\cos (\omega t)\\ v=\frac{dx}{dt}=A\omega \text{cos}(\omega t)-B\omega \sin (\omega t)\end{array}}$

Las condiciones iniciales son las siguientes: la plataforma y el bloque parten en el instante t=0 de la posición x₀=-y_e con velocidad v₀. Resolvemos el sistema de dos ecuaciones con dos incógnitas para determinar A y B.

${\displaystyle \begin{array}{l}x=-\frac{g}{{\omega }^2}+\frac{v_0}{\omega }\sin (\omega t)+\left(x_0+\frac{g}{{\omega }^2}\right)\cos (\omega t)\\ v=v_0\text{cos}(\omega t)-\left(x_0\omega +\frac{g}{\omega }\right)\sin (\omega t)\end{array}}$

La posición más baja y más alta del conjunto formado por el bloque y la plataforma se alcanza en los instante t₂ y t₃ cuando v=0,

${\displaystyle \tan (\omega t)=\frac{v_0\omega }{x_0{\omega }^2+g}{t}_2=\frac{1}{\omega }\left(\pi -\arctan \left|\frac{v_0\omega }{x_0{\omega }^2+g}\right|\right)t_3=\frac{1}{\omega }\left(2\pi -\arctan \left|\frac{v_0\omega }{x_0{\omega }^2+g}\right|\right)}$

y vale

${\displaystyle \begin{array}{l}{x}_2=-\frac{1}{{\omega }^2}\left(g+\sqrt{{(x_0{\omega }^2+g)}^2+{(v_0\omega )}^2}\right)\\ x_3=-\frac{1}{{\omega }^2}\left(g-\sqrt{{(x_0{\omega }^2+g)}^2+{(v_0\omega )}^2}\right)\end{array}}$

Para obtener estas expresiones, se emplean las relaciones trigonométricas,

${\displaystyle \cos \theta =\frac{1}{\sqrt{1+{\tan }^2\theta }}\sin \theta =\frac{\tan \theta }{\sqrt{1+{\tan }^2\theta }}}$

• como ωt₂ es un ángulo del segundo cuadrante, el seno es positivo y el coseno es negativo.

• como ωt₃ es un ángulo del cuarto cuadrante, el seno es negativo y el coseno es positivo.

Ejemplo:

Volvemos sobre el sistema formado por

• Un bloque de masa m=10 kg
• Una plataforma de masa M=20 kg
• Un muelle de constante elástica k=2000 N/m

El bloque se deja caer desde una altura de 1 m sobre el nivel del muelle sin deformar, que tomamos como origen.

1. Posición de equilibrio de la plataforma M sobre el muelle de constante k.

20·9.8=2000·y_e por lo que y_e=9.8 cm

2. La velocidad antes del choque del bloque

El bloque cae desde una altura de 1.098 m, su velocidad es

v₁=4.64 m/s

3. Choque del bloque con la plataforma

10·4.64=(10+20)·v₀ por lo que v₀=1.546 m/s ó 154.6 cm/s

4.  Condiciones iniciales

t=0, x₀=-0.098 m, v₀=1.546 m/s, y

${\displaystyle \omega =\sqrt{\frac{k}{(M+m)}}=8.165\text{rad/s}}$

Con estos datos tenemos

La ecuación del movimiento es

x=-14.7-18.94·sin(8.16·t)+4.9·cos(8.16·t) cm

• La posición más baja del conjunto bloque-plataforma se alcanza en el instante t₂=0.22 s y vale x₂=-34.26 cm

• La posición más alta del conjunto bloque-plataforma se alcanza en el instante t₃=0.61 s y vale x₃=4.86 cm

La posición más baja se vuelva a alcanzar en los instantes t₂+nP,  siendo P el periodo de la oscilación y n un número entero positivo. La posición más alta se vuelva a alcanzar en los instantes t₃+nP.

Actividades

Se introduce:

• La masa de la plataforma en kg, en el control de edición titulado Masa plataforma
• La masa del bloque en kg, en el control de edición titulado Masa del bloque
• La constante elástica del muelle que soporta a la plataforma en N/m, en el control de edición titulado Constante elástica.
• El bloque se deja caer desde la posición y= 1 m=100 cm.

Se pulsa el botón titulado Inicio, el programa verifica los datos introducidos y si son correctos se pulsa a continuación, el botón titulado Empieza.

Cada vez que se realice un nueva "experiencia", se cambian los datos y se pulsa el botón titulado Inicio.

Se sugiere emplear los botones titulados Paso y Pausa para detener el programa en cualquier momento y para ejecutar el programa paso a paso. Primero, observaremos la caída del bloque, su choque contra la plataforma y finalmente, el movimiento oscilatorio del conjunto bloque-plataforma y muelle.

A la derecha del applet, se representa la posición en función del tiempo del bloque y la plataforma cuando empiezan a oscilar. Podemos medir, la amplitud, el periodo y apreciar la fase inicial.

En la parte superior del applet, se representa la energía del sistema, el nivel cero de energía potencial se ha situado en la base del muelle elástico, 50 cm por debajo del origen. De este modo, las energías potenciales son siempre positivas, y se puede apreciar visualmente las transformaciones entre los distintos tipos de energía, así como la pérdida de energía en el momento del choque.

• La energía del bloque y de la plataforma se representa en forma de una barra de dos colores, la parte roja representa la energía potencial y la parte azul la energía cinética. La longitud de la barra representa la energía total de la partícula.
• La barra de color verde representa la energía potencial elástica del muelle.

 

Curso Interactivo de Física en Internet © Ángel Franco García