El regulador centrífugo
El regulador centrífugo de la figura, está constituido por cuatro barras articuladas de masa despreciable y de la misma longitud l, que giran alrededor de un eje vertical, estando el sistema de barras fijado al punto B. El cuerpo de masa m' que puede deslizar sin rozamiento a lo largo del eje, está apoyado en un resorte de constante k. Las bolas en las articulaciones A de las barras son iguales y de masa m. Cuando el sistema está en reposo C coincide con O y BO mide 2l.
- Calcular la deformación del resorte cuando el sistema gira con velocidad angular ω.
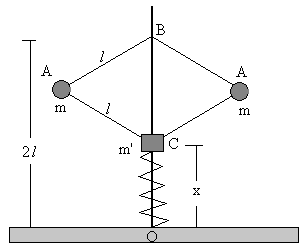
Descripción
Formularemos la ecuación de la dinámica de cada una de las dos bolas, y el equilibrio del cuerpo m' que desliza a lo largo del eje.
- Movimiento de la bola
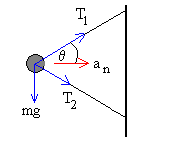La bola describe un movimiento circular de radio l cosθ , siendo θ el ángulo
formado por las barras y la horizontal. La aceleración normal de la
bola es
an=ω2 l cosθ
Por otra parte, la bola está en equilibrio en la dirección vertical.
Las ecuaciones que describen la dinámica de la bola son:
T1cosθ+T2cosθ=man
T1senθ=T2senθ+mg
- Equilibrio del cuerpo que desliza a lo largo del eje
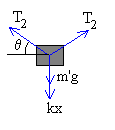El cuerpo que desliza a lo largo del eje está en equilibrio, la
resultante de las fuerzas que actúan sobre el mismo es cero.
2T2sinθ=kx+m'g
Ahora relacionamos el ángulo θ con x.
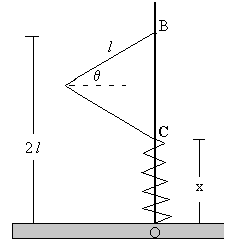
La relación entre el ángulo θ con x y l, tal como se deduce de la figura, es
2lsinθ+x=2l
De las ecuaciones que describen la dinámica del sistema se despeja el valor de x.
El valor x de la deformación del muelle viene señalado en una regleta por una flecha.
Ejemplo:
Calcular la deformación del muelle x, con los datos siguientes del regulador centrífugo
| Longitud de la varilla, l | 0.6 m |
| Masa de una bola, m | 1.5 kg |
| Masa del bloque que desliza, m’ | 2.5 kg |
| Constante elástica del muelle, k | 310 N/m |
| Velocidad angular de rotación, ω | 15 rad/s |
Actividades
Se introduce
- La constante elástica del muelle, en el control de edición titulado Cte. elástica.
- La velocidad angular de rotación, actuando sobre la barra de desplazamiento o introduciendo un valor en el control de edición titulado V. angular.
- La longitud de la varilla está fijada en l=0.6 m
- La masa del bloque que desliza está fijada en m'=2.5 kg
- La masa de cada una de las bolas está fijada en m=1.5 kg
Se pulsa el botón titulado Empieza
El regulador centrífugo empieza a girar, y una flecha marca sobre una regleta la deformación del muelle.
Activando la casilla titulada Vectores, se muestra las fuerzas que actúan sobre las bolas y sobre el cuerpo deslizante.
Comprobar que el resultado proporcionado por el programa interactivo, coincide con el obtenido al resolver el problema aplicando las ecuaciones que describen el equilibrio del cuerpo deslizante y la dinámica del movimiento circular de la bola.