• Inicio
• Dinámica
• Fuerza de rozamiento

Fuerza de rozamiento en un plano inclinado

En esta página analizamos detalladamente un problema muy común en un curso de Física cuya solución no se suele presentar de forma completa.

Un bloque de masa m₁ se sitúa sobre un plano inclinado de ángulo θ. El bloque está conectado a otro bloque de masa m₂ que cuelga de su otro extremo mediante una cuerda inextensible que pasa por una polea ideal (de rozamiento y momento de inercia despreciables). Sabiendo que el coeficiente de rozamiento entre el bloque de masa m₁ y el plano inclinado es μ, estudiar el movimiento del sistema.

 

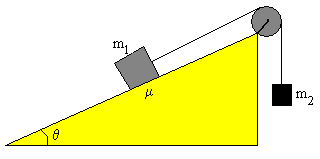
Por razón de simplicidad, supondremos que los coeficientes de rozamiento estático y cinético tienen el mismo valor μ.

Descripción

Tenemos analizar dos posibles situaciones

1. Cuando el bloque de masa m₁ está en movimiento
2. Cuando el bloque de masa m₁ está en reposo sobre el plano inclinado

Para dibujar de forma correcta el sentido de la fuerza de rozamiento, se ha de tener en cuenta que:

• Cuando el bloque desliza, la fuerza de rozamiento es siempre de sentido contrario al vector velocidad.
• Si el bloque de masa m₁ está en reposo, la fuerza de rozamiento es de sentido contrario a la resultante de las otras fuerzas que actúan sobre el bloque.

1.-El bloque de masa m₁ desliza sobre el plano inclinado

• Movimiento del bloque a lo largo del plano, hacia arriba

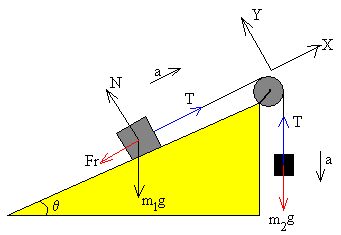
La ecuación del movimiento del bloque que cuelga de masa m₂ es  
m₂g-T=m₂a

La ecuación del movimiento del bloque de masa m₁ que desliza hacia arriba es
T-m₁g·sinθ-Fr=m₁a

La reacción del plano vale N-m₁g·cosθ=0
y la fuerza de rozamiento F_r=μ·N

 Despejamos la aceleración a

 ${\displaystyle a=g\frac{m_2-m_1\sin \theta -\mu m_1\cos \theta }{m_2+m_1}}$

• Movimiento del bloque a lo largo del plano, hacia abajo

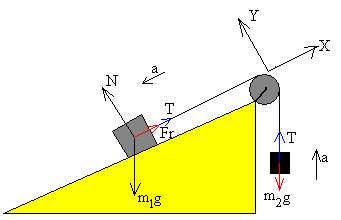
La fuerza de rozamiento cambia de sentido. Cambiamos el signo la fuerza de rozamiento en la fórmula de la aceleración

${\displaystyle a=g\frac{m_2-m_1\sin \theta +\mu m_1\cos \theta }{m_2+m_1}}$

Alternativamente, podemos volver a plantear las ecuaciones del movimiento a partir del esquema de la figura.

2.- El bloque de masa m₁ está en reposo sobre el plano inclinado

En este caso la tensión de la cuerda es igual al peso T=m₂g

La fuerza de rozamiento se opone a la resultante de las otras dos fuerzas opuestas:

• la tensión de la cuerda m₂g
• la componente del peso m₁gsinθ
   

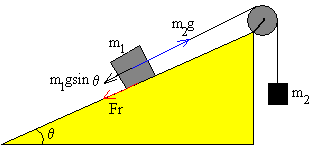La componente del peso es menor que la tensión de la cuerda, la fuerza de rozamiento se opone a que el cuerpo se mueva a lo largo del plano inclinado hacia arriba.

Si m₂g> m₁gsinθ    entonces  m₂g- m₁gsinθ-F_r=0    (1)

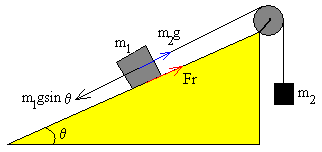La componente del peso es mayor que la tensión de la cuerda, la fuerza de rozamiento se opone a que el cuerpo se mueva hacia abajo.

Si m₂g< m₁gsinθ    entonces  m₂g-m₁gsinθ+F_r=0    (2)

La fuerza de rozamiento es nula para el ángulo θ que cumple que m₂g=m₁gsinθ. 

3.-Cuando el bloque de masa m₁ empieza a deslizar a lo largo del plano

Variando el ángulo de inclinación θ del plano inclinado llega un momento en el que el bloque empieza a deslizar, en ese momento la fuerza de rozamiento alcanza su valor máximo
F_r=μN= μm₁gcosθ

Vamos  a determinar el o los ángulos de plano inclinado para los cuales el bloque de masa m₁ va a empezar a deslizar a lo largo de dicho plano 

Llamando m=m₂/m₁, la ecuación de equilibrio de fuerzas (1) se escribe 

m-sinθ- μcosθ=0

Teniendo en cuenta que cos²θ=1-sin²θ. Despejando cosθ y elevando al cuadrado, nos queda la ecuación de segundo grado en sinθ.

(1+μ²)sin²θ-2msinθ+(m²-μ²)=0

La misma ecuación de segundo grado se obtiene a partir de la ecuación de equilibrio de fuerzas (2)

${\displaystyle \sin \theta =\frac{m\pm \mu \sqrt{1-m^2+{\mu }^2}}{1+{\mu }^2}}$

La ecuación de segundo grado tiene dos raíces reales siempre que el discriminante sea positivo
1-m²+μ²≥0.

Para que las dos raíces reales sean positivas se tiene que cumplir que la raíz más pequeña sea positiva, esto es

${\displaystyle m\ge \mu \sqrt{1-m^2+{\mu }^2}}$

Elevando al cuadrado ambos miembros, obtenemos la desigualdad equivalente
m≥ μ

• El discriminante es siempre positivo para m<1 es decir, para m₂<m₁

• En cambio, si m>1, es decir, si m₂>m₁ las raíces reales existen si μ²≥m²-1

Ejemplos

m=0.6 y μ=0.4

La fuerza de rozamiento es nula para el ángulo m=sinθ, es decir, para θ=36.9º.

Al resolver la ecuación de segundo grado, se obtienen dos ángulos θ₁=12.05 y θ₂=55.66

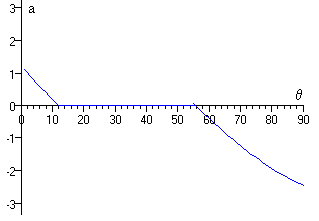El ángulo θ₁ cumple la ecuación de equilibrio (2)
m-sinθ+μcosθ=0

El ángulo θ₂ cumple la ecuación de equilibrio (1)
m-sinθ- μcosθ=0

Así pues, en el intervalo angular entre θ₁ =12.05º a θ₂=55.66º el bloque de masa m₁ está en reposo sobre el plano inclinado.

 

 

• θ<θ₁

Para todos los ángulos θ del plano inclinado menores que θ₁ se cumple que  m₂g>m₁gsinθ o bien, que  m>sinθ  y el bloque desliza a lo largo del plano inclinado hacia arriba a>0. Por ejemplo, cuando θ=10º

${\displaystyle a=g\frac{m-\sin \theta -\mu \cos \theta }{m+1}=0.20{\text{m/s}}^{\text{2}}}$

• θ>θ₂

Para todos los ángulos θ del plano inclinado mayores que θ₂, se cumple que  m₂g<m₁gsinθ o bien, que  m<sinθ  y el bloque desliza  a lo largo del plano inclinado hacia abajo a<0. Por ejemplo, cuando θ=70º

${\displaystyle a=g\frac{m-\sin \theta +\mu \cos \theta }{m+1}=-1.24{\text{m/s}}^{\text{2}}}$

m=1.1 y μ=0.6

El discriminante de la ecuación de segundo grado es positivo ya que se cumple que μ²≥m²-1

Se obtienen dos ángulos θ₁=39.64 y θ₂=78.43

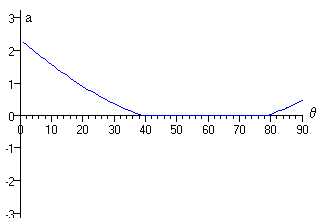Como m>sinθ  para todos los ángulos de inclinación θ ambas soluciones cumplen la primera ecuación de equilibrio (1) m-sinθ- μcosθ=0

Así pues, en el intervalo angular entre θ₁ =39.64º a θ₂=78.43º el bloque de masa m₁ está en reposo sobre el plano inclinado.

 

 

 

 

• θ<θ₁

Para todos los ángulos θ del plano inclinado menores que θ₁ el bloque desliza  a lo largo del plano inclinado hacia arriba a>0. Por ejemplo, cuando θ=30º

${\displaystyle a=g\frac{m-\sin \theta -\mu \cos \theta }{m+1}=0.37{\text{m/s}}^{\text{2}}}$

• θ>θ₂

Para todos los ángulos θ del plano inclinado mayores que θ₂ el bloque desliza a lo largo del plano inclinado hacia arriba a>0. Por ejemplo, cuando θ=80º 

a=0.05 m/s²

m=1.2 y μ=0.6

No existen raíces reales, el discriminante de la ecuación de segundo grado es negativo ya que no se cumple que μ²≥m²-1

El bloque desliza a lo largo del plano inclinado hacia arriba para cualquier ángulo θ. Por ejemplo, cuando θ=30º 

a=0.80 m/s²

Actividades

Se introduce 

• La masa m₂ del bloque, en el control de edición titulado Masa bloque
• El coeficiente de rozamiento μ, en el control de edición titulado Coef. rozamiento
• La masa m₁ del bloque que está sobre el plano inclinado se ha fijado en 1 kg.

Se pulsa el botón titulado Nuevo

Cada vez que se cambia

• El ángulo θ del plano inclinado, se introduce un valor en el control de edición titulado Ángulo y se pulsa Enter o Retorno, o se actúa sobre la barra de desplazamiento.

Se pulsa el botón titulado Empieza

En la parte izquierda del applet, observamos la representación gráfica de la aceleración del bloque en función del ángulo de inclinación del plano inclinado θ.

Un punto de color rojo sobre la curva azul, indica el valor del ángulo θ y de la aceleración a para la “experiencia” actual.

En la parte superior derecha, se representan las fuerzas que actúan sobre el bloque situado sobre el plano inclinado. Lo más importante es observar el sentido de la fuerza de rozamiento (flecha de color rojo) en los distintos casos que se han estudiado en el apartado Ejemplos.

stokesApplet aparecerá en un explorador compatible con JDK 1.1.

Referencias

Wehrbein W. Frictional forces on an incline plane. Am. J. Phys. 60 (1) January 1992, pp. 57-58

Curso Interactivo de Física en Internet © Ángel Franco García