Fuerzas no conservativas
Para darnos cuenta del significado de una fuerza no conservativa, vamos a compararla con la fuerza conservativa peso.
El peso es una fuerza conservativa.
Calculemos el trabajo de la fuerza peso cuando la partícula se traslada de A hacia B, y a continuación cuando se traslada de B hacia A.
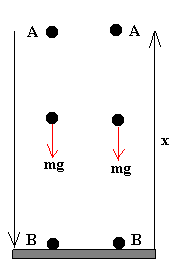
WAB=mg x
WBA=-mg x
El trabajo total a lo largo el camino cerrado A-B-A, WABA es cero.
La fuerza de rozamiento es una fuerza no conservativa
Cuando la partícula se mueve de A hacia B, o de B hacia A la fuerza de rozamiento es opuesta al movimiento, el trabajo es negativo por que la fuerza es de signo contrario al desplazamiento.
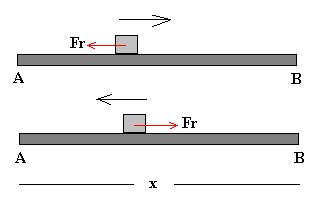 WAB=-Fr x
WAB=-Fr x
WBA=-Fr x
El trabajo total a lo largo del camino cerrado A-B-A, WABA es distinto de cero
WABA=-2Fr x
Balance de energía
En general, sobre una partícula actúan fuerzas conservativas Fc y no conservativas Fnc. El trabajo de la resultante de las fuerzas que actúan sobre la partícula es igual a la diferencia entre la energía cinética final menos la inicial.
El trabajo de las fuerzas conservativas es igual a la diferencia entre la energía potencial inicial y la final
Aplicando la propiedad distributiva del producto escalar obtenemos que
El trabajo de una fuerza no conservativa modifica la energía mecánica (cinética más potencial) de la partícula.
Ejemplo 1:
Un bloque de masa 0.2 kg inicia su movimiento hacia arriba, sobre un plano de 30º de inclinación, con una velocidad inicial de 12 m/s. Si el coeficiente de rozamiento entre el bloque y el plano es 0.16. Determinar:
-
la longitud x que recorre el bloque a lo largo del plano hasta que se para
-
la velocidad v que tendrá el bloque al regresar a la base del plano
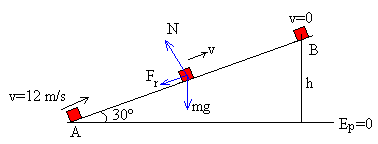
Cuando el cuerpo asciende por el plano inclinado
-
La energía del cuerpo en A es EA=½0.2·122=14.4 J
-
La energía del cuerpo en B es EB=0.2·9.8·h=1.96·h =0.98·x J
-
El trabajo de la fuerza de rozamiento cuando el cuerpo se desplaza de A a B es
W=-Fr·x=-μ·mg·cosθ·x=-0.16·0.2·9.8·cos30·x=-0.272·x J
De la ecuación del balance energético W=EB-EA, despejamos x=11.5 m, h=x·sin30º=5.75 m
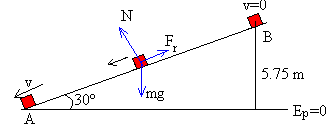
Cuando el cuerpo desciende
-
La energía del cuerpo en B es EB=0.2·9.8·h=1.96·h =0.98·x=0.98·11.5=11.28 J
-
La energía del cuerpo en la base del plano EA==½0.2·v2
-
El trabajo de la fuerza de rozamiento cuando el cuerpo se desplaza de B a A es
W=-Fr·x=-μ·mg·cosθ·x=-0.16·0.2·9.8·cos30·11.5=-3.12 J
De la ecuación del balance energético W=EA-EB, despejamos v=9.03 m/s.
Ejemplo 2:
Una partícula de masa m desliza sobre una superficie en forma de cuarto de circunferencia de radio R, tal como se muestra en la figura.
Las fuerzas que actúan sobre la partícula son:
-
El peso mg
-
La reacción de la superficie N, cuya dirección es radial
-
La fuerza de rozamiento Fr, cuya dirección es tangencial y cuyo sentido es opuesto a la velocidad de la partícula.
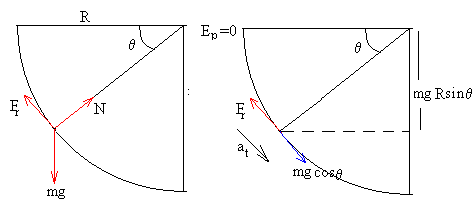
Descomponiendo el peso mg, a lo largo de la dirección tangencial y normal, escribimos la ecuación del movimiento de la partícula en la dirección tangencial
mat=mg·cosθ-Fr
Donde at=dv/dt es la componente tangencial de la aceleración. Escribimos en forma de ecuación diferencial la ecuación del movimiento
Calculamos el trabajo Wr realizado por la fuerza de rozamiento. La fuerza de rozamiento es de sentido contrario al desplazamiento
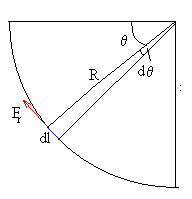 Teniendo en cuenta que el deslazamiento es un pequeño
arco de circunferencia dl=R·dθ y que
Teniendo en cuenta que el deslazamiento es un pequeño
arco de circunferencia dl=R·dθ y que
El trabajo realizado por la fuerza no conservativa Fr vale
Si el móvil parte del reposo v=0, en la posición θ=0. Cuando llega a la posición θ
-
La energía cinética se ha incrementado en mv2/2.
-
La energía potencial ha disminuido en mgRsinθ.
El trabajo de la fuerza de rozamiento es igual a la diferencia entre la energía final y la energía inicial o bien, la suma de la variación de energía cinética más la variación de energía potencial.
El trabajo total de la fuerza de rozamiento cuando la partícula describe el cuarto de círculo es
Para un cálculo explícito del trabajo de la fuerza de rozamiento véase "Movimiento sobre un cúpula semiesférica con rozamiento"
