Conductor esférico en un campo eléctrico uniforme
Una esfera conductora está situada en un campo eléctrico uniforme, determinar la distribución de carga en la superficie del conductor. La solución a este problema es mucho más compleja que el procedimiento de las imágenes que hemos descrito en la página anterior, por lo que solamente se darán los resultados.
La ley de Gauss se puede expresar de forma diferencial o de forma integral. Cuando se expresa la ley de Gauss en forma diferencial en un espacio en el que la densidad de carga libre es cero, tenemos la ecuación de Laplace.
Campo eléctrico
Se resuelve la ecuación de Laplace en coordenadas esféricas con las siguientes condiciones de contorno
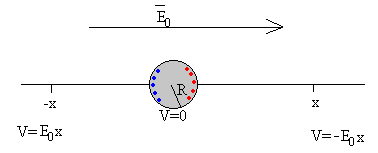
- V=0 para r=R, en la superficie de la esfera
- V=-E0x cuando x es grande y la influencia del campo eléctrico de la esfera es despreciable. (Recuérdese que el potencial disminuye en la dirección del campo eléctrico uniforme E0).
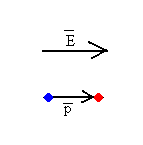El campo eléctrico total, es la suma del campo eléctrico uniforme más el
campo producido por un dipolo de momento dipolar p=4π ε0E0R3 situado en el centro de la esfera.
Las componentes del campo eléctrico en coordenadas polares son
Potencial
El potencial en un punto P de coordenadas (r, θ ) es
Como vemos cumple que cuando r se hace grande, el potencial V tiende a –E0rcosθ =-E0x, y para r=R, el potencial es V=0.
Carga inducida
La densidad superficial de carga inducida en la esfera conductora es el producto de ε0 veces el valor de Er para r=R.
σ =3ε0E0cosθ
La carga inducida neta q en la esfera conductora se obtiene multiplicando la densidad de carga por el elemento de superficie esférica comprendido entre θ y θ +dθ , sumando para todos los ángulos comprendidos entre 0 y π.
la carga neta q=0 es cero.
Actividades
En el applet se muestra las líneas de fuerza y equipotenciales de un campo eléctrico uniforme paralelo al eje X (horizontal) y una esfera conductora conectada a tierra.
Se introduce
- el valor del campo eléctrico E0, en el control de selección titulado Campo.
- el radio R de la esfera se ha fijado en la unidad.
Se pulsa el botón titulado Nuevo
Observamos como se perturba el campo cuando se introduce una esfera conductora en el espacio en el que existe un campo eléctrico uniforme.
Pulsando en la casilla titulada Carga inducida obtenemos una imagen de la distribución de carga inducida, es decir, de la variación de la densidad de carga σ en función del ángulo θ . Los puntos de color rojo representan las cargas positivas y los azules las cargas negativas.
Al aplicar un campo eléctrico, los portadores de carga negativa de la esfera conductora se mueve en el sentido contrario al campo, hacia la izquierda, dejando la parte derecha del conductor cargada positivamente. Tenemos de este modo un dipolo, formado por una distribución espacial y simétrica de dos cargas iguales y opuestas. La densidad de carga positiva es máxima para θ =0, y la densidad de carga negativa es máxima para θ =π . La densidad de carga es nula para θ =π /2. Como vemos no hay líneas de fuerza que lleguen o salgan de esta posición.
Referencias
Lorrain P. Corson D. Campos y ondas electromagnéticas. Selecciones Científicas (1972), págs. 179-18