Espiras en un campo magnético variable con el tiempo (II)
En este pagina, se describe un experimento que nos permite comprobar la ley de inducción de Faraday.
donde Φ es el flujo a través de una espira, y N es el número de espiras iguales.
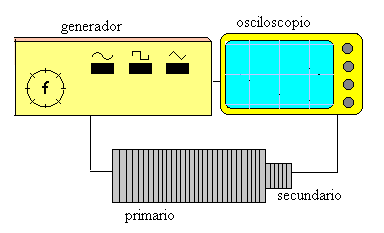
El experimento consta de un generador de ondas en el que podemos seleccionar la forma de la onda (cuadrada, triangular o senoidal). El generador está unido a un solenoide (primario) que produce un campo magnético variable con el tiempo. Esta bobina está acoplada a otra (secundario) cuyo número de espiras podemos elegir entre las siguientes: 300, 600, 900, 1200. Podemos también cambiar la frecuencia en el generador dentro de un cierto intervalo.
En la pantalla de un osciloscopio se representa la diferencia de potencial variable producida por el generador y la fem en el secundario.
Descripción
Analizaremos cada una de las señales que produce el generador
Señal de forma cuadrada
Para crear un campo magnético constante y por tanto, un flujo constante, usamos la señal cuadrada del generador. La señal cuadrada se caracteriza por que durante medio periodo el potencial vale V, y durante el otro medio periodo vale –V.
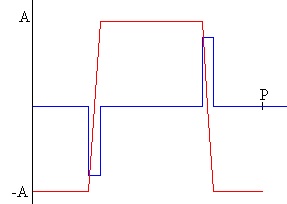 La señal no es exactamente cuadrada, ya que no pasa del potencial
positivo al negativo y viceversa, en un instante concreto, sino durante un intervalo de
tiempo, pequeño comparado con el periodo de la señal.
La señal no es exactamente cuadrada, ya que no pasa del potencial
positivo al negativo y viceversa, en un instante concreto, sino durante un intervalo de
tiempo, pequeño comparado con el periodo de la señal.
Si el flujo Φ =cte. Aplicando la ley de Faraday obtenemos la fem inducida
Cuando el potencial del generador es constante, el campo magnético es constante en el primario, el flujo a través del secundario es constante, la fem es nula.
Señal de forma triangular
Cuando el potencial del generador crece linealmente (en color rojo), el flujo a través de cada espira del secundario crece linealmente, la fem inducida en el secundario (en color azul) tiene un valor constante negativo (parte izquierda de la figura)
Si el flujo Φ =at, (0<t< P/2) , a es la pendiente
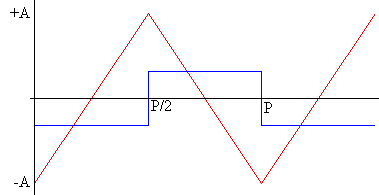
Cuando el potencial del generador decrece linealmente (en color rojo), la fem en el secundario (en color azul) muestra un valor constante positivo (parte central de la figura)
Si Φ =a·(P-t), (P/2<t< P)
Señal de forma senoidal
Este caso ya lo hemos estudiado en la página precedente, espiras en un campo magnético variable con el tiempo
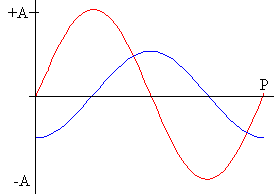 El campo magnético producido por el primario y por tanto, el flujo a
través de cada espira del secundario tiene forma senoidal (en rojo)
El campo magnético producido por el primario y por tanto, el flujo a
través de cada espira del secundario tiene forma senoidal (en rojo)
Φ =Φ0 sin(ω t)
La fem en el secundario (en azul) es la derivada cambiada de signo del flujo
Influencia de los distintos parámetros
- Influencia de la amplitud
La fem inducida es proporcional a la amplitud A de la señal.
- Influencia del número de espiras del secundario
La fem es proporcional al número de espiras N en el secundario.
- Efecto de la frecuencia
La frecuencia f no tiene efecto en la señal cuadrada, pero tiene efecto en la señal triangular y senoidal. Al aumentar la frecuencia, disminuye el periodo, y aumenta la pendiente, por lo que la fem es mayor.
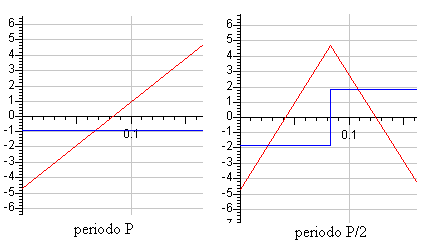
En la figura, se compara la fem de una señal triangular de periodo P (en color rojo), y de la misma señal de periodo P/2. La pendiente de la recta se ha duplicado y por tanto, la fem en el secundario (en color azul) se duplica.
En las señales senoidales, al derivar el flujo Φ =Φ0 sin(ω t) respecto del tiempo, se obtiene una fem. que es proporcional a la frecuencia angular ω.
Actividades
Se introduce
- La frecuencia, entre 3 y 10 unidades, actuando sobre la barra de desplazamiento titulada Frecuencia
- La amplitud, actuando sobre la barra de desplazamiento o introduciendo un valor entre 3.5 y 10 unidades en el control de edición titulado Amplitud
- El número de espiras, 300, 600, 900 y 1200 espiras, N. espiras
- Forma de la señal: activar uno de los botones de radio titulados: Cuadrada, Triangular y Senoidal.
Se pulsa el botón titulado Gráfica
Se representa
- en color rojo, la diferencia de potencial producida por el generador
- en color azul, la fem en el secundario
Referencias
Trumper R., Gelbman M. Investigating electromagnetic induction through a microcumputer-based laboratory.. Phys. Educ. 35(2) March 2000, pp 90-95
