Varilla que se mueve en un campo magnético uniforme (I)

En la páginas anteriores, hemos visto como se obtenía una fem variando el campo magnético con el tiempo. Ahora vamos a ver que como se obtiene una fem agrandando o reduciendo el camino cerrado que atraviesa un campo magnético constante en el tiempo.

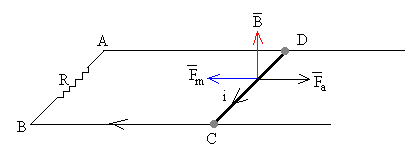
Sea un conductor rectilíneo que desliza con velocidad constante v por dos guías tal como se muestra en la figura (más abajo). Las guías están conectadas por uno de sus extremos para formar un circuito cerrado.

Vamos a obtener el valor de la fem y el sentido de la corriente inducida por dos procedimientos:

La ley de Faraday para calcular la fem y la ley de Lenz para determinar el sentido de la corriente inducida
A partir de la fuerza sobre los portadores de carga positivos que se mueven con la varilla en el seno de un campo magnético uniforme

La ley de Faraday

Supongamos que el campo magnético B es constante y es perpendicular al plano determinado por las guías y la varilla. El flujo del campo magnético a través del circuito de forma rectangular ABCD señalado en la figura es

Φ=B · S =B a x

donde a·x es el área del rectángulo ABCD.

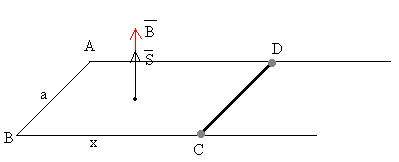
fem7_1.gif (1852 bytes)

Al moverse la varilla CD la dimensión x del rectángulo aumenta o disminuye, haciendo variar el flujo con el tiempo. De acuerdo a la ley de Faraday, la fem inducida en el circuito ABCD es

V E =− dΦ dt =−Ba dx dt =−Bav

Sentido de la corriente inducida

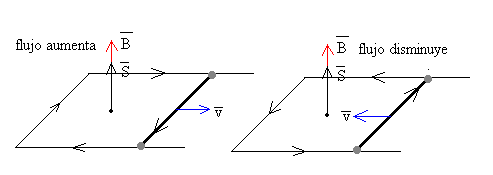
fem7_3.gif (2772 bytes)

Si la varilla se mueve hacia la derecha, aumenta el área S, lo mismo le ocurre al flujo Φ, el sentido de la corriente inducida es el de las agujas del reloj.

Si la varilla se mueve hacia la izquierda, el área S disminuye, lo mismo le ocurre al flujo Φ, el sentido de la corriente inducida es contrario al de las agujas del reloj.

Fuerza sobre los portadores de carga

Vamos a obtener el mismo resultado por otro procedimiento distinto, examinando las fuerzas sobre los portadores de carga positivos existentes en la varilla.

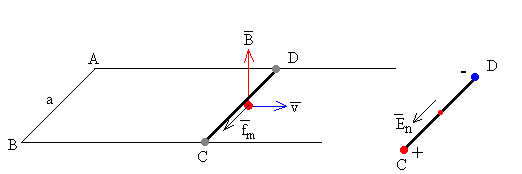
fem7_2.gif (2317 bytes)

Al moverse la varilla hacia la derecha, con velocidad v en el seno de un campo magnético uniforme B, los portadores de carga se mueven con la misma velocidad horizontal. La fuerza sobre dichos portadores es

f=q·v×B

Como v y B son perpendiculares, el módulo de la fuerza es

f=qvB.

La dirección de la fuerza es la de la varilla y el sentido de D a C.

Tenemos por tanto un sistema de "bombeo" de carga positiva desde D hacia el extremo C, análogo al del generador de Van de Graaff desde la base hacia la esfera conductora. De menos potencial a más potencial.

El campo E_n que impulsa las cargas (fuerza por unidad de carga) es E_n=vB y solamente existe en el tramo DC de la varilla

V ε = ∮ E n ·dl= ∫ D C vB·dx=vBa

El campo E_n tiene origen magnético y es no conservativo.

fem7_4.gif (1506 bytes) La diferencia de potencial entre el extremo C y D es V_C-V_D=vBa, siendo a la distancia entre las guías. Como vemos C está a un potencial mayor que D.

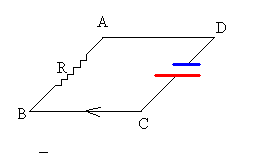
Al conectar C y D mediante las guías, la corriente fluye espontáneamente de C a D pasando por B y A.

Tenemos el equivalente a una batería que produce una fem V_E=vBa. Si la resistencia del circuito es R, la intensidad de la corriente inducida es

i= V ε R = vBa R

Estudio energético

Cuando circula por la varilla CD una corriente i, el campo magnético B ejerce una fuerza F m =i u ^ t ×BL .El vector unitario u_t que señala el sentido de la corriente y el campo B son mutuamente perpendiculares, la longitud del conductor es a, por lo que el módulo de la fuerza magnética es F_m=iBa. Su sentido es el indicado en la figura (hacia la izquierda si la varilla se mueve hacia la derecha)

Para que la varilla se mueva con velocidad constante v, hemos de ejercer una fuerza F_a igual y de sentido contrario a F_m.

fem7_5.gif (1971 bytes)

La energía mecánica por unidad de tiempo (potencia) suministrada será

P a = F a ⋅v=iBav= B 2 a 2 v 2 R

La energía por unidad de tiempo (potencia disipada por efecto Joule) en la resistencia será P_R=i²R

P R = B 2 a 2 v 2 R

En el estado estacionario, la intensidad de la corriente es constante, la energía por unidad de tiempo suministrada mecánicamente al mover la varilla, se disipa en la resistencia en forma de calor.

Si consideramos la varilla como una batería cuya fem es V_ε=vBa. La potencia suministrada por la fem será P_ε=V_ε·i

P E = B 2 a 2 v 2 R

Actividades

El applet describe el movimiento de una varilla que desliza sin rozamiento sobre dos guías paralelas. El sistema formado por la varilla y las guías esta contenido en un plano paralelo a los polos de un imán.

Se introduce:

El campo magnético en gauss. Inicialmente el campo magnético apunta en la dirección vertical, hacia arriba. Si introducimos un valor negativo, se cambia la polaridad de los imanes y el campo magnético apunta hacia abajo.
La velocidad de la varilla en cm/s. Este valor puede ser positivo o negativo. Si es positivo la varilla se mueve de izquierda a derecha y si es negativo se mueve de derecha a izquierda.
La distancia entre las guías en cm. Un número menor que 15.

Se pulsa el botón titulado Empieza.

La corriente inducida se representa mediante el movimiento de pequeños círculos de color rojo (portadores de carga positivos). También se representa la fuerza sobre un portador de carga positivo mediante una flecha de color rojo. La velocidad se representa mediante una flecha de color negro, y el campo mediante una flecha de color azul.

Ejemplo:

B=40 gauss=0.004 T
v=5 cm/s=0.05 m/s
a=10 cm=0.1 m

La fem vale V_є=0.04·0.05·0.1=2·10^-5 V

Se recomienda al lector que dibuje sobre un papel el sistema formado por la varilla y las guías, situados en un campo magnético, con el siguiente convenio:

Un círculo con un punto en su interior, indica que el campo magnético es perpendicular al plano del papel que apunta hacia el lector.
Un círculo con una cruz, representa un campo magnético perpendicular al plano del papel que apunta hacia dentro, en sentido contrario al anterior.

Dibujar el vector velocidad en el centro de la varilla
Dibujar la fuerza sobre un portador de carga positivo situado en el interior de la varilla y a continuación, el sentido de su movimiento (de la corriente inducida)

Alternativamente

Razonar si el flujo aumenta o disminuye
Aplicar la ley de Lenz y dibujar el sentido de la corriente inducida
Comprobar que en ambos casos coincide el sentido de la corriente inducida dibujada.
Comparar la respuesta con la proporcionada por el programa interactivo.

FemApplet aparecerá en un explorador compatible JDK 1.1