Circuito en serie LCR. Resonancia

Se ha estudiado el comportamiento de una bobina, un condensador y una resistencia cuando se conectan por separado a un generador de corriente alterna.

En esta página, estudiaremos el comportamiento de un sistema formado por los tres elementos dispuestos en serie y conectados a un generador de corriente alterna de amplitud V₀ y frecuencia angular ω .

v=V₀ sin(ω t)

Circuito LCR en serie

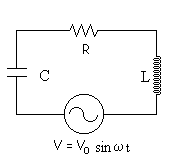Dibujamos el diagrama de vectores teniendo en cuenta:

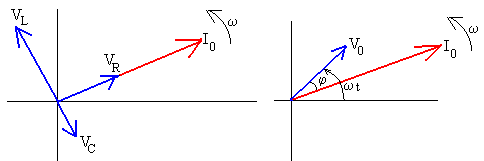
que la intensidad que pasa por todos los elementos es la misma,
que la suma (vectorial) de las diferencias de potencial entre los extremos de los tres elementos nos da la diferencia de potencial en el generador de corriente alterna.

El vector resultante de la suma de los tres vectores es

V 0 = V R 2 + ( V L − V C ) 2 = I 0 R 2 + ( ω L− 1 ω C ) 2

Se denomina impedancia del circuito al término

Z= R 2 + ( ω L− 1 ω C ) 2

de modo que se cumpla una relación análoga a la de los circuitos de corriente continua

V₀=I₀·Z.

El ángulo que forma el vector resultante de longitud V₀ con el vector que representa la intensidad I₀ es

tan⁡ϕ= V L − V C V R = ω L− 1 ω C R

Las expresiones de la fem y de la intensidad del circuito son

v= V 0 sin⁡(ω t) i= I 0 sin⁡(ω t−ϕ)

La intensidad de la corriente en el circuito está atrasada un ángulo φ respecto de la fem que suministra el generador.

Actividades

En el applet se introducen los siguientes datos:

Resistencia en Ω
Capacidad en microfaradios (10^-6 F)
Autoinducción en mH (10^-3 H)
El cociente ω/ω₀entre la frecuencia ω del generador y la frecuencia propia del circuito ω₀

ω 0 = 1 LC

Se pulsa el botón titulado Empieza.

Se observa los valores instantáneos de la corriente i en el circuito LCR y de la diferencia de potencial (ddp) V del generador a medida que transcurre el tiempo.

A la izquierda, como proyecciones sobre el eje vertical de los vectores rotatorios que representan a la intensidad y la ddp.
A la derecha, la representación gráfica de los valores de la intensidad y de la ddp en función del tiempo.

Observar las relaciones de fase entre la intensidad y la ddp en el generador en los siguientes casos

ω =ω₀
ω >ω₀
ω <ω₀

Ejemplo:

R=1.5 Ω
L=5·10^-3 H
C=4·10^-6 F
ω=1.01·ω₀

La frecuencia propia del circuito es

ω 0 = 1 5· 10 −3 ·4· 10 −6 =7071 rad/s

La frecuencia del generador es ω=1.01·ω₀=7142 rad/s

La impedancia vale

Z= 1.5 2 + ( 7142·5· 10 −3 − 1 7142· 4· 10 −6 ) 2 =1.65 Ω

El desfase es

tan⁡ϕ= 7142 ·5· 10 −3 − 1 7142·4· 10 −6 1.5 ϕ=0.44 rad=25.2º

FemApplet aparecerá en un explorador compatible JDK 1.1