]> El anillo de Thomson (I)
SiguienteAnterior

Coeficiente de inducción mutua

En la página anterior, se describió el origen de la fuerza sobre el anillo, pero no se calculó esta fuerza. En esta página, vamos a explicar cómo se puede medir el coeficiente de inducción mutua M que precisamos para calcular la corriente Ia en el anillo, y la componente radial del campo magnético Br producido por la bobina, ambos factores intervienen en la fuerza Fz que ejerce dicho campo sobre la corriente inducida en el anillo.

Componente radial del campo

La componente radial del campo Br producido por la bobina en la posición (y, z) es

B r = μ 0 2π I 1 r 1 ·z ∫ −π/2 π/2 sin⁡φ ( r 1 2 + z 2 + y 2 −2 r 1 y·sin⁡φ ) 3/2 dφ

Si la bobina consta de N1 espiras apretadas. La componente radial del campo Br en la posición que ocupa el anillo (r2, z) vale

B r = μ 0 2π N 1 I 1 r 1 ·z ∫ −π/2 π/2 sin⁡φ ( r 1 2 + z 2 + r 2 2 −2 r 1 r 2 ·sin⁡φ ) 3/2 dφ

El valor del campo Br se puede calcular también de forma indirecta

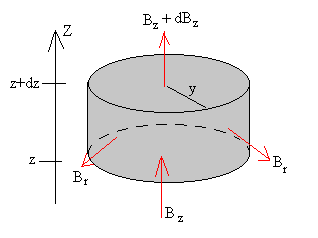La ley de Gauss aplicada al campo magnético afirma que el flujo del campo magnético a través de una superficie cerrada es nulo, ya que no existen cargas magnéticas aisladas análogas a las eléctricas.

∮ B⋅dS=0

Tomemos una superficie cerrada de forma cilíndrica de radio y, de altura dz. Como se aprecia en la figura, el campo magnético entra por la base inferior Ф(z) y sale por la superficie lateral Br·2πydz  y por la base superior Ф(z+dz) de la superficie cerrada

El flujo total será

Φ(z+dz)−Φ(z)+ B r ·2πydz=0 B r =− 1 2π y dΦ(z) dz

Como Ф(z+dz)=(Bz+dBz)πy2 y Ф(z)=Bz·πy2

B r =− y 2 ∂ B z ∂z

Que nos da la relación entre las componentes radial Br y vertical Bz del campo magnético producido por la bobina.

El objetivo de esta sección, es obtener una expresión aproximada del coeficiente de inducción mutua M entre la bobina y la espira en función de la altura z del anillo.

Una vez obtenida M podemos calcular el valor aproximado de la componente radial Br del campo magnético en la posición (r2, z) que ocupa el anillo.

B r =− I 1 2π  r 2 dM(z) dz

Siendo I1 la corriente que circula por la bobina

Medida del coeficiente de inducción mutua

Para medir el flujo Ф(z) del campo magnético producido por la bobina que atraviesa el anillo, o el coeficiente el coeficiente de inducción mutua M=Ф(z)/I1 a distintas alturas z, diseñamos el siguiente experimento.

Medimos la amplitud de la fem V02 producida en una bobina exploradora de N2 espiras del mismo radio que el anillo. Si por la bobina circula una corriente de amplitud I01 y de frecuencia angular ω.

V 2 =− dΦ dt =− N 2 M d I 1 dt =− N 2 M I 01 ω·cos⁡(ω t) M= V 02 N 2 I 01 ω

Actividades

Se introduce

Se pulsa el botón titulado Inicio

Se pulsa el botón titulado Empieza

Se mide la amplitud de la fem producida en la bobina exploradora (parte superior del applet) y se determina el coeficiente de inducción mutua

Ejemplo:

Para z=5 cm, V02=72.59·10-6 V

M= V 02 N 2 I 01 ω   M= 71.24· 10 −6 1·1·2π·50 =0.227· 10 −6  H

Los pares de datos:

se guardan en el control área de texto situado a la izquierda del applet

 Para cada radio del anillo, se obtiene una tabla de valores como la siguiente

Radio r2=1.5 cm
Posición z del anillo (cm) Coef. inducción mutua M·106 H
1.0 1.177
2.0 0.814
3.0 0.523
4.0 0.345
5.0 0.227
6.0 0.155
7.0 0.109
8.0 0.079
9.0 0.059
10.0 0.045

Se pulsa el botón titulado Gráfica

El programa interactivo calcula por el procedimiento de regresión exponencial la función M=a·exp(bz) que mejor ajusta a los datos “experimentales”. Se precisan como mínimo tres pares de datos.

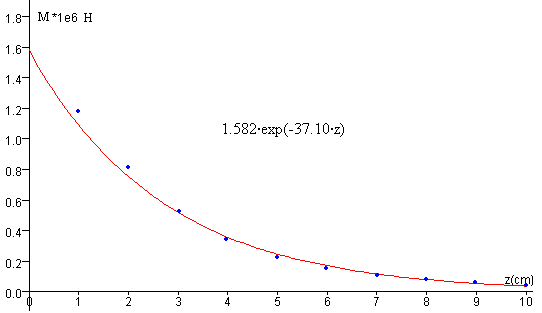
En este caso es la función

M=1.582·exp(-37.10·z)

donde z está en m y M en 10-6 H

Su valor para z=0.05 es M=0.2475·10-6 H

El valor del campo radial Br en la posición z=5 cm es

B r =− I 1 2π  r 2 dM(z) dz                 B r = I 1 2π·0.015 1.582·37.1·exp⁡(−37.1·0.05)· 10 −6 =97.430· 10 −6 I 1  T

La intensidad de la corriente en el anillo en el estado estacionario es

I 2 =− M· I 01 ω R 2 + ω 2 L 2 ( Rcos⁡(ω t)+ω Lsin⁡(ω t) )  

Supongamos que R=3.6·10-4 Ω, y L=6.5·10-7 H y ω=2π·50 rad/s y I01=10 A

I2=-1.634cos(2π·50·t)-0.927sin(2π·50·t)

La fuerza sobre el anillo es

Fz=-2π·r2·I2·Br=2π·0.015·(1.634cos(2π·50·t)+0.927sin(2π·50·t))· 97.43·10-6·10·sin(2π·50·t)=
1.50·10-4·cos(2π·50·t)·sin(2π·50·t)+ 8.51·10-5·sin2(2π·50·t)

Teniendo en cuenta que, el valor medio de <sin(ωt)·cos(ωt)>=0, y el valor medio de <sin2(ωt)>=1/2. La fuerza media vale

<Fz>=4.255·10-5 N=0.043 mN

SolenoideApplet aparecerá en un explorador compatible JDK 1.1

Arrastre con el puntero del ratón la flecha de color azul

SiguienteAnterior