• Inicio
• Electromagnetismo
• Materiales

Método de Montecarlo. Variable aleatoria continua

Si colocamos el dipolo en un campo eléctrico E, actúan sobre él un par de fuerzas, cuyo momento tiende a orientar al dipolo en la dirección del campo. Sin embargo, esta tendencia estará contrarrestada por la agitación térmica de las moléculas. Para cada campo y temperatura tendremos una orientación media resultado del compromiso entre ambas tendencias contrapuestas. La energía del dipolo en el campo eléctrico es

La energía de un dipolo en un campo eléctrico E es U= -p·E= -pEcosθ 

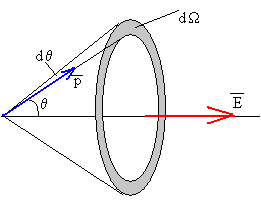
Como el ángulo θ puede tener cualquier valor entre 0 y π, las energías de los estados disponibles no son discretas sino que varían de forma continua. La probabilidad P(θ) de que el vector momento dipolar p apunte según un ángulo comprendido entre θ y θ +dθ es proporcional a

${\displaystyle \exp \left(\frac{pE\cos \theta }{kT}\right)}$

La constante de proporcionalidad se determina a partir de la condición de que los dipolos con dicha energía apuntan con sus vectores momento dipolar en todas las direcciones del espacio cuyos ángulos están comprendidos entre θ y θ +dθ. En la última figura, se representa el ángulo sólido dΩ correspondiente a dicha apertura angular.

${\displaystyle P(\theta )d\theta =\frac{\exp \left(\frac{pE\cos \theta }{kT}\right)}{{\displaystyle \underset{0}{\overset{\pi }{\int }}\exp \left(\frac{pE\cos \theta }{kT}\right)}d\Omega }}$

La polarización de la sustancia dieléctrica será

${\displaystyle P=Np{\displaystyle \underset{0}{\overset{\pi }{\int }}\cos \theta ·P(\theta )·d\theta }}$

Siendo N el número de moléculas y el resto de la fórmula, la componente media del momento dipolar en la dirección del campo. La integración conduce a la conocida ecuación de Langevin

${\displaystyle P=Np\left(\coth u-\frac{1}{u}\right)u=\frac{pE}{kT}}$

En el caso límite u<<<1, es decir, para campos eléctricos débiles o temperaturas elevadas dicha función se puede aproximar a la recta

${\displaystyle P=\frac{N{p}^2}{3k}\frac{E}{T}}$

la polarización es una función lineal del cociente campo/temperatura, esta fórmula es análoga a la expresión de la ley de Curie para los materiales paramagnéticos.

Cuando u es grande la ecuación de Langevin tiende hacia un valor límite constante. Para campos eléctricos intensos o bajas temperaturas los dipolos están alineados, es decir, predomina el efecto orientador del campo.

P=Np

Para aplicar el método de Montecarlo hemos de transformar la variable aleatoria angular continua θ, distribuida con probabilidad P(θ) en el intervalo [0, π) en una variable aleatoria uniformemente distribuida γ en el intervalo [0, 1), véase el apartado variable aleatoria continua. La fórmula de transformación es

${\displaystyle \gamma ={\displaystyle \underset{0}{\overset{\theta }{\int }}P(\theta )·d\theta }=\frac{\exp (u)-\exp (u\cos \theta )}{\exp (u)-\exp (-u)}}$

Despejamos de la fórmula anterior cosθ.

${\displaystyle \cos \theta =\frac{1}{u}\left(\gamma \exp (-u)+(1-\gamma )\exp (u)\right)}$

La clase que describe el sistema físico

Los miembros dato de la clase Dielectrico son el momento dipolar po de las moléculas del material dieléctrico polar, y el número de partículas nParticulas que forman la sustancia dieléctrica. Se pasan al constructor estos dos datos, para crear un objeto de la clase Dielectrico que describa una muestra de dicha sustancia.

public class Dielectrico {
    private double po;         //momento dipolar
    public int nParticulas;
//números aleatorios
    private Random rnd=new Random();
    private static final double COEFICIENTE=0.7246;     

    public Dielectrico(int nParticulas, double momento) {
        this.nParticulas=nParticulas;
        po=momento;
    }
//funciones miembro ...
}

La constante COEFICIENTE, es el producto de 10^-30 (unidad del momento dipolar) por 10⁷ (unidad del campo eléctrico) dividido por la constante de Boltzmann 1.38 10^-23.

La función miembro sorteo devuelve el cosθ de cada molécula particular. Dicho valor se calcula mediante la última fórmula del apartado anterior.

    private double sorteo(double campo, double temperatura){
        double u=COEFICIENTE*po*campo/temperatura;
        double coseno=Math.log((1-aleatorio)*Math.exp(u)+Math.random()*Math.exp(-u))/u;
        return coseno;
    }

La función momentoDipolarMedio calcula y devuelve el momento dipolar medio de una muestra significativa de moléculas dipolares para cada campo eléctrico y temperatura absoluta. Se suma todos los cosenos devueltos por la función sorteo, los multiplica por el momento dipolar po de las moléculas y los divide entre el número de moléculas. Como caso particular, consideramos aquél en el que la temperatura es cero, todos los momentos dipolares apuntan en la dirección del campo.

    public double momentoDipolarMedio(double campo, double temperatura){
        if(temperatura<=0.0){
            return po;
        }
        double media=0.0;
        for(int i=0; i<nParticulas; i++){
            media+=sorteo(campo, temperatura);
        }
        return (media*po)/nParticulas;
    }

Para utilizar la clase Dielectrico fijaremos el momento dipolar de las moléculas de la sustancia y la intensidad del campo eléctrico que actúa sobre la muestra de material dieléctrico y variaremos la temperatura.

Creamos un objeto di de la clase Dielectrico y le pasamos en su constructor el número de moléculas de la muestra y el tipo de material dieléctrico por ejemplo, el agua que tiene un momento dipolar de 6.2 (x 10^-30 C m). Fijamos el campo eléctrico cuya intensidad vale 40 (x 10⁷ N/C). El objeto di llama a la función miembro momentoDipolarMedio y le pasa la intensidad del campo y la temperatura absoluta, devolviendo el momento dipolar medio de la muestra.

        Dielectrico di=new Dielectrico(1000, 6.2);
        double campo=40.0; //en unidades 10 elevado a 7  N/C
        System.out.println("temperatura \t m. dipolar medio");
        for(double T=0.0; T<100; T+=10.0){
            System.out.println(" "+T+ " \t \t"+
			(double)Math.round(100*di.momentoDipolarMedio(campo, T))/100);
        }

Ejercicio

En la siguiente tabla se proporcionan los momentos dipolares de algunas sustancias dieléctricas

• Completar tablas en las que fijada la intensidad del campo eléctrico y el tipo de material, se obtenga el momento dipolar medio en función de la temperatura.
• Comprobar que la polarización es una función lineal del campo temperatura, para altas temperaturas o baja intensidad del campo eléctrico (un comportamiento similar a la ley de Curie)

Curso Interactivo de Física en Internet © Ángel Franco García