• Inicio
• Fluidos
• Estática
• Principio de Arquímedes

Equilibrio de una varilla parcialmente sumergida

En esta página, se estudia el equilibrio de una varilla parcialmente sumergida que está sujeta por una de sus extremos.

Consideremos una varilla delgada, de sección uniforme A y de longitud L y densidad ρ<1 que está sujeta por su  extremo P, pero que le permite moverse en el plano vertical. Vamos a analizar la situación de equilibrio cuando una parte de la varilla está sumergida en agua tal como se muestra en la figura.

El punto de sujeción está por encima de la superficie del agua

Supongamos que el extremo P de la varilla está a una altura y>0 sobre la superficie del agua y en esa posición la varilla hace un ángulo θ con el eje vertical.

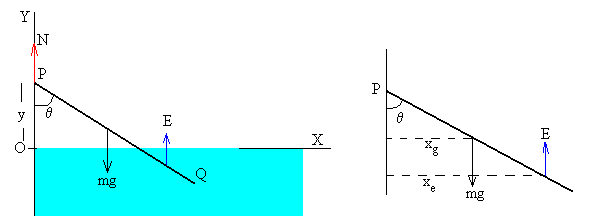
Las fuerzas que actúan sobre la varilla son:

• El peso mg=ρALg, actúa en el centro de masa de la varilla, en la posición cuya abscisa es

x_g=L/2·sinθ.

• La fuerza de empuje, E=gA·(L-y/cosθ) actúa en el centro de la porción de varilla sumergida, en la posición cuya abscisa es

${\displaystyle x_e=\left(\frac{y}{\cos \theta }+\frac{1}{2}\left(L-\frac{y}{\cos \theta }\right)\right)\sin \theta =\frac{1}{2}\left(L+\frac{y}{\cos \theta }\right)\sin \theta }$

• La reacción N se aplica en el punto P.

La barra estará en equilibrio:

• Si la resultante de todas las fuerzas es cero,

N+E=mg

• Si el momento de las fuerzas respecto del punto P es cero.

E·x_e-mgx_g+N·0=0

${\displaystyle gA\left(L-\frac{y}{\cos \theta }\right)\left(L+\frac{y}{\cos \theta }\right)\frac{\sin \theta }{2}-\rho gAL\frac{L}{2}\sin \theta =0}$

Simplificando, nos queda la ecuación

${\displaystyle \left(1-\rho -\frac{y^2}{L^2}\frac{1}{{\cos }^2\theta }\right)\sin \theta =0}$

Si y>L el primer factor entre paréntesis es distinto de cero. La posición de equilibrio se obtiene cuando senθ=0, es decir, θ=0. La barra cuelga verticalmente del punto P, sin estar sumergida

Cuando y<L el primer término puede hacerse cero cuando

${\displaystyle \cos \theta =\frac{y}{L}\frac{1}{\sqrt{1-\rho }}\le 1}$

y como el coseno tiene que ser menor o igual que la unidad se tiene que cumplir a la vez que $y\le L\sqrt{1-\rho }$ Cuando no se cumple esta condición el primer factor no es nulo y la posición de equilibrio es θ=0.

El punto de sujeción está por debajo de la superficie del agua

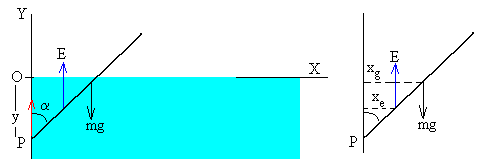
Sea y la distancia (positiva) del punto P de sujeción de la varilla al origen O

• El peso mg=ρALg, actúa en el centro de masa de la varilla, en la posición cuya abscisa es

x_g=L/2·sinα.

La fuerza de empuje, E=gA(y/cosα) actúa en el centro de la porción de varilla sumergida,  en la posición de abscisa

${\displaystyle x_e=\frac{1}{2}\frac{y}{\cos \alpha }\sin \alpha }$

Para que la varilla esté en equilibrio, el momento de estas fuerzas respecto del punto P es cero.

E·x_e-mgx_g=0

${\displaystyle gA\frac{y}{\cos \alpha }\frac{y}{\cos \alpha }\frac{\text{sin}\alpha }{2}-\rho gAL\frac{L}{2}\text{sin}\alpha =0}$

Simplificando

${\displaystyle \left(\frac{y^2}{L^2}\frac{1}{{\cos }^2\alpha }-\rho \right)\text{sin}\alpha =0}$

Si y>L el primer factor entre paréntesis no puede ser cero. La posición de equilibrio se obtiene cuando senα=0, es decir, α=0.

Cuando y<L el primer factor puede ser cero cuando

${\displaystyle \cos \alpha =\frac{y}{L}\frac{1}{\sqrt{\rho }}\le 1}$

y como el coseno tiene que ser menor o igual que la unidad se tiene que cumplir a la vez que $y\le L\sqrt{\rho }$ Cuando no se cumple esta condición el primer factor no es nulo y la posición de equilibrio es α=0.

Resumen

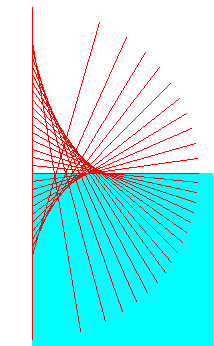En la figura, podemos ver las sucesivas posiciones de equilibrio de la varilla a medida que se cambia la posición y del punto de sujeción P. Teniendo en cuenta, que θ es el ángulo que forma la varilla con la dirección vertical y que θ=π-α, las posiciones de equilibrio son

 

El punto P de sujeción de la varilla está por encima de la superficie agua (y>0)
${\displaystyle y>L\sqrt{1-\rho }}$	θ=0
${\displaystyle y\le L\sqrt{1-\rho }}$	${\displaystyle \cos \theta =\frac{y}{L}\frac{1}{\sqrt{1-\rho }}}$
El punto P de sujeción de la varilla está por debajo de la superficie del agua (y<0)
${\displaystyle \left|y\right|>L\sqrt{\rho }}$	θ=π
${\displaystyle \left|y\right|\le L\sqrt{\rho }}$	${\displaystyle \cos \theta =\frac{y}{L}\frac{1}{\sqrt{\rho }}}$

Actividades

Se introduce

• La densidad ρ de la varilla, moviendo el dedo de la barra de desplazamiento titulada Densidad

• La posición y del punto P de sujeción de la varilla, moviendo el dedo de la barra de desplazamiento titulada Posición barra

• La longitud de la varilla se ha fijado en el programa interactivo en el valor L=1.0

Se pulsa el botón titulado Nuevo

Observamos, la varilla en su posición de equilibrio. Se muestran las fuerzas, peso de la varilla y fuerza de empuje sobre la parte sumergida.

En la parte derecha del applet, se representa el ángulo θ, (en grados) en función de la posición y del punto de sujeción. Se representa mediante un punto el estado de equilibrio, el par de valores (y, θ).

Fijamos la densidad de la varilla, y vamos cambiando la posición y del punto P de sujeción de la varilla.

Ejemplo:

Introducimos los siguientes datos

• Densidad ρ=0.3

• Posición y=-0.4 del punto P de sujeción de la varilla.

Se pulsa el botón titulado Nuevo

Como y<0, comprobamos que se cumple la condición

${\displaystyle \left|y\right|\le L\sqrt{\rho }\text{0}\text{.4}<\text{1}\text{.0}\sqrt{\text{0}\text{.3}}}$

El ángulo θ que forma la varilla con el eje vertical se obtiene de la expresión

${\displaystyle \cos \theta =\frac{y}{L}\frac{1}{\sqrt{\rho }}\cos \theta =\frac{-0.4}{1.0}\frac{1}{\sqrt{0.3}}\theta =137º}$

FluidoApplet1 aparecerá en un explorador compatible con JDK 1.1.

Referencias

Duffy B. A bifurcation problem in hydrostatics. Am. J. Phys. 61 (3) March 1993, pp. 264-269

Curso Interactivo de Física en Internet © Ángel Franco García