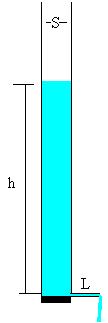
El tubo-capilar

El tubo-capilar consiste en un tubo de plástico transparente cerrado por su extremo inferior con un tapón. Perpendicularmente al tubo de plástico y en su parte inferior, se perfora y se introduce un tubo de vidrio de pequeño diámetro, que hace de capilar a través del cual se descarga la columna de fluido viscoso. Una regla colocada en su parte exterior o marcas sobre el tubo permiten medir la altura de la columna de fluido en función de tiempo.

Descripción

Partiendo de la ley de Poiseuille

G= π 8 ( p 1 − p 2 ) R 4 η L

la diferencia de presión p₁-p₂ entre los extremos del capilar es igual a la presión que ejerce la altura h de la columna de fluido de densidad ρ. Luego, p₁-p₂=ρ gh

Si G es el volumen de fluido que sale del capilar en la unidad de tiempo, la altura h de la columna de fluido disminuye, de modo que

−S dh dt = π 8 ρ gh R 4 η L

Siendo S la sección del tubo. Podemos escribir la ecuación anterior

dh dt =−λh λ= π 8 R 4 ρg ηLS

donde λ se denomina constante del tubo-capilar.

Integrado la ecuación diferencial, con la condición inicial de que en el instante t=0, la altura inicial sea h=h₀.

∫ h 0 h dh h =−λ ∫ 0 t dt h= h 0 exp⁡(−λt)

La altura de la columna de fluido h decrece exponencialmente con el tiempo t.

Tomando logaritmos neperianos

lnh=lnh₀-λt

Si realizamos la representación gráfica de lnh frente a t obtenemos una línea recta de pendiente –λ.

En el laboratorio de la E.U.I.T.I. de Eibar (véase el primer artículo citado en las referencias) se ha realizado las siguientes medidas con un tubo-capilar usando aceite de automóvil como fluido.

h(cm)	t (s)
47.5	0
42.5	29
37.5	62
32.5	101
27.5	145
22.5	197
17.5	265
12.5	355
7.5	500

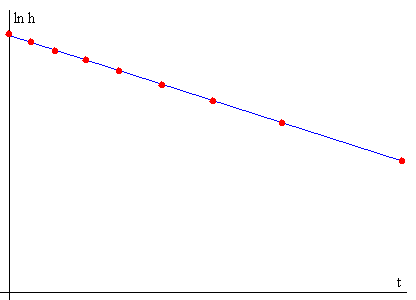Si introducimos los datos t, y ln(h) en el programa interactivo de la página Regresión lineal, obtenemos una línea recta de pendiente -0.00371, de modo que la constante λ=0.00371 s^-1.

Si disponemos de los datos relativos a

Longitud del capilar L y su radio R
Área de la sección del tubo S
Densidad del fluido ρ

Podemos despejar la viscosidad η del fluido de la fórmula que nos relaciona valor de la constante λ del tubo-capilar, con dichos parámetros, deducida al principio de este apartado.

Vida media

La vida media de unas sustancia radioactiva se define como el tiempoτ necesario para que el número de núcleos activos se reduzca a la mitad.

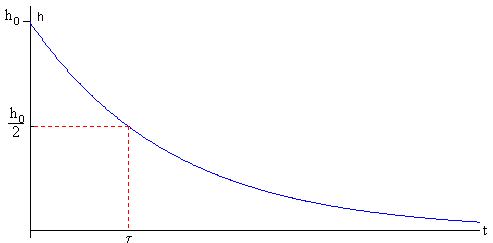
Relacionamos la vida media τ del tubo-capilar y su constante λ , poniendo h=h₀/2.

h 0 2 = h 0 exp(-λτ) τ= ln⁡2 λ

Fenómenos físicos análogos

La ecuación que describe la descarga de un tubo-capilar es similar a

Las variables físicas análogas se recogen en el siguiente cuadro

Fluidos	Electricidad	Radioactividad
h, altura de la columna de fluido	q, carga del condensador	N, número de núcleos sin desintegrar
dh/dt, velocidad de decrecimiento	i=dq/dt, intensidad de la corriente eléctrica	dN/dt, actividad radioactiva en valor absoluto
λ , constante del tubo-capilar	1/RC, constante del circuito	λ , constante de desintegración

Actividades

Se introduce

la longitud del tubo-capilar en cm, actuando en la barra de desplazamiento titulada Longitud capilar.

Se pulsa el botón titulado Nuevo.

Con el puntero del ratón se arrastra la flecha de color rojo, para establecer la altura inicial h₀ de la columna de fluido.

Se pulsa el botón titulado Empieza.

Comienza a salir el fluido por el capilar. Simultáneamente, se traza la curva que nos describe la altura de fluido en función del tiempo. Podemos observar que es una exponencial decreciente. Se marca el tiempo que tarda en alcanzarse la mitad de la altura inicial, lo que se conoce como vida media.

FluidoApplet1 aparecerá en un explorador compatible con JDK 1.1.

Se arrastra con el puntero del ratón la flecha de color rojo

Referencias

Franco A. Analogías Físicas (Mecánica, Electricidad, Fluidos) . Documentación E.I. (Enseñanzas Integradas). Vol 6 (3),1982, págs. 63-69.

Smithson J. R., Pinkston E. R., Half-life of a water column as a laboratory exercise in exponential decay. Am. J. Phys. 28 (1960) pp. 740-742.