Ecuación diferencial de segundo orden
Muchas páginas del Curso Interactivo de Física describen situaciones físicas en las que se aplica el procedimiento numérico de Runge-Kutta para resolver una ecuación diferencial de segundo orden.
Descripción
Vamos a aplicar el procedimiento de Runge-Kutta a una ecuación diferencial de segundo orden.
con las condiciones iniciales
Una ecuación diferencial de segundo orden es equivalente a un sistema de dos ecuaciones diferenciales de primer orden, por lo que aplicaremos el mismo esquema.
Comparando esta tabla con la de un sistema de dos ecuaciones diferenciales de primer orden, vemos que la segunda columna es la misma, excepto por cambio de nombre de la función, f en vez de g, y de la variable, v en vez de y. En la primera columna, las variables k1, k2, k3, k4pueden calcularse directamente sin efectuar llamadas a una función.
La jerarquía de clases
La definición de la clase abstracta RungeKutta con la función miembro resolver es, la siguiente.
public abstract class RungeKutta {
double h;
public RungeKutta(double h) {
this.h=h;
}
public void setPaso(double h){
this.h=h;
}
public void resolver(Estado e){
//variables auxiliares
double k1, k2, k3, k4;
double l1, l2, l3, l4;
//estado en el instante t
double x=e.x;
double v=e.v;
double t=e.t;
k1=h*v;
l1=h*f(x, v, t);
k2=h*(v+l1/2);
l2=h*f(x+k1/2, v+l1/2, t+h/2);
k3=h*(v+l2/2);
l3=h*f(x+k2/2, v+l2/2, t+h/2);
k4=h*(v+l3);
l4=h*f(x+k3, v+l3, t+h);
x+=(k1+2*k2+2*k3+k4)/6;
v+=(l1+2*l2+2*l3+l4)/6;
t+=h;
//estado en el instante t+h
e.t=t;
e.x=x;
e.v=v;
}
abstract public double f(double x, double y, double t);
}
|
La definición de la clase cuyos miembros dato nos sirven para guardar el estado del sistema es similar a la clase definida en el apartado sistema de dos ecuaciones diferenciales de primer orden con el mismo propósito, cambiando el miembro y por la derivada de x, que hemos llamado v.
public class Estado {
public double t;
public double x;
public double v;
public Estado(double t, double x, double v) {
this.t=t;
this.x=x;
this.v=v;
}
}
|
Ejemplos
-
Oscilaciones libres
La ecuación diferencial que describe un oscilador armónico y su solución para unas condiciones iniciales fijadas es
donde ω0 es la frecuencia angular, y el periodo del movimiento es P=2π/ω0.
La clase denominada Oscilador que describirá un oscilador armónico tendrá como miembro dato, la frecuencia angular, y derivará de la clase base RungeKutta, ya que el comportamiento de un oscilador armónico viene descrito por una ecuación diferencial de segundo orden. La clase Oscilador definirá la función f declarada abstracta en la clase base.
public class Oscilador extends RungeKutta{
protected double w0; //frecuencia angular
public Oscilador(double h, double w0){
super(h);
this.w0=w0;
}
public double f(double x, double v, double t){
return (-w0*w0*x);
}
}
|
Examinemos el comportamiento de un oscilador que en el instante inicial t=0, se encuentra en la posición de máximo desplazamiento x=A, y se suelta con velocidad inicial cero v=0. La amplitud A y la fase inicial φ se calculan, a partir de las condiciones iniciales especificadas, que pueden ser distintas de las señaladas.
Podemos experimentar con un oscilador de frecuencia angular ω0 de 2 rad/s, lo que corresponde a un periodo P=2π/ω0de π s, calculemos la posición y la velocidad del oscilador en el instante t= 2s, tomando como paso h el valor de 0.01.
public class Aplicacion {
public static void main(String[] args) {
double h=0.01; //paso
double w0=2.0; //frecuencia propia oscilaciones libres
double t=2.0; //resolver la e. d. hasta este instante
//Situación inicial
double x0=1.5; //posición inicial
double v0=0.0; //velocidad inicial
Estado e=new Estado(0.0, x0, v0);
//oscilaciones libres
System.out.println("Oscilaciones libres");
Oscilador os=new Oscilador(h, w0);
for(int i=0; i<t/h; i++){
os.resolver(e);
}
System.out.println("posición aproximada "+e.x);
System.out.println("velocidad aproximada "+e.v);
// valor exacto
double fi=Math.atan(w0*x0/v0);
double A=x0/Math.sin(fi);
double x=A*Math.sin(w0*t+fi);
double v=A*w0*Math.cos(w0*t+fi);
System.out.println("posición exacta "+x);
System.out.println("velocidad exacta "+v);
}
} |
-
Oscilaciones amortiguadas
Si además consideramos que existe un rozamiento que se describe en términos de una fuerza proporcional a la velocidad, la ecuación diferencial del oscilador amortiguado se escribe.
En vez de crear una nueva clase Amortiguado que sustituya a la clase Oscilador, podemos pensar que un oscilador amortiguado, es una clase especial de oscilador, y por tanto la clase que lo describe, derivará de Oscilador, le añadirá el miembro dato g (por γ), que da cuenta de la intensidad de las fuerzas de rozamiento, y además, redefine la función f.
public class Amortiguado extends Oscilador{
protected double g;
public Amortiguado(double h, double g, double w0){
super(h, w0);
this.g=g;
}
public double f(double x, double v, double t){
return (-2*g*v-w0*w0*x);
}
}
|
En la figura, se muestra la jerarquía de clases.
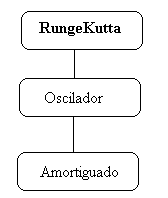
Sea por ejemplo, un oscilador armónico amortiguado que tiene los datos ω0=2, γ=0.5, y las condiciones iniciales en el instante son t=0, x=1.5, y v=0. Tomando un paso h de anchura 0.1, se puede comparar la posición del móvil en el instante t, con la deducida a partir de la solución analítica de la ecuación diferencial
La amplitud A y la fase inicial φ se calculan a partir de las condiciones iniciales especificadas.
public class Aplicacion {
public static void main(String[] args) {
double h=0.01; //paso
double w0=2.0; //frecuencia propia oscilaciones libres
double g=0.5; //cte de amortiguamiento
double t=2.0; //resolver la e. d. hasta este instante
//Situación inicial
double x0=1.5; //posición inicial
double v0=0.0; //velocidad inicial
Estado e=new Estado(0.0, x0, v0);
//oscilaciones amortiguadas
System.out.println("Oscilaciones amortiguadas");
Amortiguado am=new Amortiguado(h, g, w0);
for(int i=0; i<t/h; i++){
am.resolver(e);
}
System.out.println("posición aproximada "+e.x);
System.out.println("velocidad aproximada "+e.v);
// valor exacto
double w=Math.sqrt(w0*w0-g*g);
double fi=Math.atan(w*x0/(v0+g*x0));
double A=x0/Math.sin(fi);
double x=A*Math.exp(-g*t)*Math.sin(w*t+fi);
System.out.println("posición exacta "+x);
double v=A*Math.exp(-g*t)*(-g*Math.sin(w*t+fi)+w*Math.cos(w*t+fi));
System.out.println("velocidad exacta "+v); }
} |
