El método de Simpson
Algunas páginas del Curso Interactivo de Física describen situaciones físicas en las que es necesario calcular numéricamente una integral definida por el procedimiento de Simpson.
Descripción
En este procedimiento, se toma el intervalo de anchura 2h, comprendido entre xi y xi+2, y se sustituye la función f(x) por la parábola que pasa por tres puntos (xi, yi), (xi+1, yi+1), y (xi+2, yi+2).
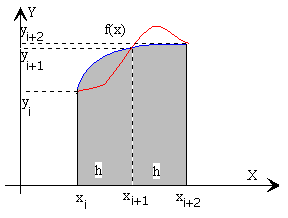
Calculamos la contribución a la integral del primer intervalo (x0, x0+2h) y generalizaremos al resto de los intervalos.
La ecuación de la parábola y=ax2+bx+c que pasa por los puntos (x0, y0), (x0+h, y1), (x0+2h, y2) es
Este sistema de tres ecuaciones con tres incógnitas, se reduce a
Despejamos el coeficiente a, y 2ax0+b
Sustituimos la curva por la porción de parábola en el intervalo (x0, x0+2h). La integral aproximada vale
En general, el valor del área aproximada, en el intervalo (xi, xi+2h) sombreada en la figura, es
El área aproximada en el intervalo [a, b] es
o bien, agrupando términos
El primer paréntesis, contiene la suma de los extremos, el segundo, la suma de los términos de índice impar, y el tercero la suma de los términos de índice par. En el método de Simpson, el número de divisiones n debe de ser par. En el caso de que el usuario introduzca un número impar el programa lo convierte en el número par siguiente.
La jerarquía de clases
Crearemos una clase base abstracta denominada Simpson, que defina la función miembro integral que calcula la integral definida de cualquier función f(x) por el procedimiento de Simpson.
public abstract class Simpson {
public double integral(double a, double b, int n){
if(n%2==1) n++; //n es par
double h=(b-a)/n;
double suma=f(a)+f(b);
for(int i=1; i<n; i+=2){
suma+=4*f(a+i*h);
}
for(int i=2; i<n; i+=2){
suma+=2*f(a+i*h);
}
return (suma*h/3);
}
abstract public double f(double x);
}
|
En la clase derivada Funcion definiremos la función f(x) cuya integral deseamos calcular.
public class Funcion extends Simpson{
public double f(double x){
return Math.cos(x);
}
} |
Para hallar la integral definida de esta función entre los límites 0 y π /2, creamos un objeto de la clase Funcion mediante new y llamamos desde este objeto a la función integral pasándole en el primer argumento el límite inferior 0, en el segundo el límite superior, π /2, y por último, el número 10 de divisiones (par) del intervalo.
public class Aplicacion {
public static void main(String[] args) {
double resultado=new Funcion().integral(0.0, Math.PI/2, 10);
System.out.println("integral "+resultado);
}
}
|
