Integrales dobles
Queremos calcular la integral doble
el área comprendida entre las curvas y=c(x), y=d(x) y las rectas x=a y x=b
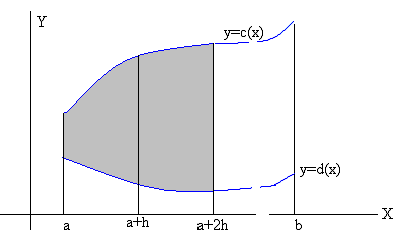
Si aplicamos el procedimiento de Simpson, se divide el intervalo [a, b] en un número par de intervalos, el área en los dos primeros intervalos es
Ejemplo.
Comprobar que
La jerarquía de clases
Crearemos una clase base abstracta denominada SimpsonDoble, que defina la función miembro integral que calcula la integral definida de cualquier función f(x) por el procedimiento de Simpson.
public abstract class SimpsonDoble {
public double integral(double a, double b, int n, int m){
double h=(b-a)/(2*n);
double J1=0.0, J2=0.0, J3=0.0;
double x, y;
double HX, K1, K2, K3, Q, L;
for(int i=0; i<=2*n; i++){
x=a+i*h;
HX=(d(x)-c(x))/(2*m);
K1=f(x, c(x))+f(x, d(x));
K2=0.0;
K3=0.0;
for(int j=1; j<=2*m-1; j++){
y=c(x)+j*HX;
Q=f(x, y);
if(j%2==0) K2+=Q;
else K3+=Q;
}
L=(K1+2*K2+4*K3)*HX/3;
if(i==0 || i==2*n) J1+=L;
else{
if(i%2==0) J2+=L;
else J3+=L;
}
}
double J=h*(J1+2*J2+4*J3)/3;
return J;
}
abstract public double f(double x, double y);
abstract public double c(double x);
abstract public double d(double x);
}
|
En la clase derivada Funcion definiremos la función f(x) cuya integral deseamos calcular.
En la clase derivada Funcion1 definiremos la función f(x) cuya integral deseamos calcular.
ppublic class Funcion extends SimpsonDoble{
public double f(double x, double y){
return Math.exp(y/x);
}
public double c(double x){
return(x*x*x);
}
public double d(double x){
return(x*x);
}
}
public class Funcion1 extends SimpsonDoble{
public double f(double x, double y){
return (x*x+y*y*y);
}
public double c(double x){
return(x);
}
public double d(double x){
return(2*x);
}
} |
Creamos un objeto de la clase Funcion mediante new y llamamos desde este objeto a la función integral pasándole en el primer argumento el límite inferior 0.1, en el segundo el límite superior, 0.5 y por último, el número de divisiones (par) de los intervalos. Creamos un objeto de la clase Funcion1...
public class Aplicacion {
public static void main(String[] args) {
double resultado=new Funcion().integral(0.1, 0.5, 50, 50);
System.out.println("integral "+resultado);
resultado=new Funcion1().integral(0, 1.0, 2, 4);
|
Referencias
Análisis numérico. Burden R. L., Douglas Faires J., International Thomson Editores (1998), págs. 229-236
