• Inicio
• Sólido rígido
• Movimiento general

Movimiento de un disco que gira y desliza sobre una superficie plana y horizontal

En esta página, se analiza el movimiento de un disco que desliza sobre una superficie plana y horizontal y que a la vez gira alrededor de su eje.

Vamos a estudiar el papel de la fuerza de rozamiento entre la superficie del disco y el plano sobre el que desliza, se observa que:

1. Cuando el disco no gira, continúa su movimiento rectilíneo de traslación hasta que se detiene.

2. Cuando el disco solamente gira, continua su movimiento de rotación con su centro de masa en reposo, hasta que se para.

3. El tiempo que tarda en detenerse el disco depende de su velocidad inicial y del coeficiente de rozamiento.

4. Cuando el disco tiene ambos tipos de movimiento, el centro del disco continúa su movimiento rectilíneo de traslación y el disco gira alrededor del eje perpendicular al disco y que pasa por su centro, hasta que ambos movimientos se detienen simultáneamente, independientemente de las velocidades iniciales.

Esta última propiedad parece sorprendente, pero vamos a demostrar que los movimientos de traslación y de rotación del disco no son independientes, sino que están fuertemente acoplados.

Este ejemplo, aunque sencillo en su formulación no tiene una solución analítica. Para describir la posición y la velocidad del disco en función del tiempo hay que resolver, aplicando procedimientos numéricos, las ecuaciones del movimiento.

Ecuaciones del movimiento del aro

Recordaremos que

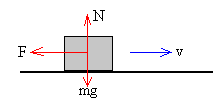
Un bloque de masa m que se mueve sobre una superficie horizontal. La fuerza de rozamiento que se opone al movimiento es F=μN, con N=mg

Comenzamos nuestro estudio con un aro de masa m_a y de radio R, como etapa previa antes de abordar el disco. El centro del aro se mueve con velocidad v, y gira alrededor de un eje perpendicular al plano del aro y que pasa por el centro, con velocidad angular ω.

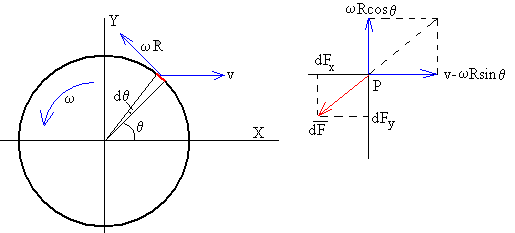
El vector velocidad de un punto P cuya posición angular es θ,

v_p=(v-ωRsinθ)i+(ωRcosθ)j

La fuerza de rozamiento dF que actúa sobre un elemento de masa dm se opone al movimiento de dicho elemento, su dirección es la misma que la velocidad v, y de sentido contrario.

${\displaystyle dF=-\mu ·dm·g\frac{v_p}{v_p}}$

Si m_a es la masa del aro, la masa dm del elemento de longitud R·dθ, es dm=m_a·dθ/(2π)

Resultantes de las fuerzas que actúan sobre el aro

Las componentes del vector fuerza dF sobre dicho elemento son

${\displaystyle \begin{array}{l}d{F}_x=-\frac{m_a}{2\pi }\mu g\frac{v-\omega R\text{sin}\theta }{\sqrt{v^2+{\omega }^2{R}^2-2v\omega R\text{sin}\theta }}d\theta \\ d{F}_y=-\frac{m_a}{2\pi }\mu g\frac{\omega R\text{cos}\theta }{\sqrt{v^2+{\omega }^2{R}^2-2v\omega R\text{sin}\theta }}d\theta \end{array}}$

Las componentes de la fuerza resultante sobre el aro son

${\displaystyle \begin{array}{l}{F}_x=-\frac{m_a}{2\pi }\mu g{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{v-\omega R\text{sin}\theta }{\sqrt{v^2+{\omega }^2{R}^2-2v\omega R\text{sin}\theta }}d\theta }\\ F_y=-\frac{m_a}{2\pi }\mu g{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{\omega R\text{cos}\theta }{\sqrt{v^2+{\omega }^2{R}^2-2v\omega R\text{sin}\theta }}d\theta }\end{array}}$

Por simetría F_y=0, lo que se confirma resolviendo la segunda integral.

Ecuación del movimiento del centro de masas del aro

${\displaystyle \begin{array}{l}{m}_a\frac{dv}{dt}=F_x\\ \frac{dv}{dt}=-\frac{\mu g}{2\pi }{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{v-\omega R\text{sin}\theta }{\sqrt{v^2+{\omega }^2{R}^2-2v\omega R\text{sin}\theta }}d\theta }\end{array}}$

Momento de las fuerzas sobre los elementos del aro, respecto de su centro.

${\displaystyle \begin{array}{l}dM=R\times dF=R\times \left(-\mu ·dm·g\frac{v}{v}\right)=-\mu ·dm·g\left(R\cos \theta i+R\text{sin}\theta j\right)\times \\ \left(\frac{v-\omega R\text{sin}\theta }{\sqrt{v^2+{\omega }^2{R}^2-2v\omega R\text{sin}\theta }}i+\frac{\omega R\text{cos}\theta }{\sqrt{v^2+{\omega }^2{R}^2-2v\omega R\text{sin}\theta }}j\right)=\\ -\mu ·dm·g\left(\frac{\omega R^2{\text{cos}}^{\text{2}}\theta }{\sqrt{v^2+{\omega }^2{R}^2-2v\omega R\text{sin}\theta }}-\frac{R\text{sin}\theta (v-\omega R\text{sin}\theta )}{\sqrt{v^2+{\omega }^2{R}^2-2v\omega R\text{sin}\theta }}\right)k=\\ -\frac{m_a}{2\pi }\mu g\left(\frac{R(\omega R-v\text{sin}\theta )}{\sqrt{v^2+{\omega }^2{R}^2-2v\omega R\text{sin}\theta }}\right)d\theta ·k\end{array}}$

El momento total de las fuerzas sobre los elementos del aro, respecto del centro es

${\displaystyle M=-\frac{m_a}{2\pi }\mu g{\displaystyle \underset{0}{\overset{2\pi }{\int }}\left(\frac{R(\omega R-v\text{sin}\theta )}{\sqrt{v^2+{\omega }^2{R}^2-2v\omega R\text{sin}\theta }}\right)d\theta }}$

Su dirección es la del eje de rotación (ejeZ), y su sentido es contrario al de la velocidad angular ωdel aro.

Ecuación de la dinámica de rotación I(dω/dt)=M. Donde I=m_a·R² es el momento de inercia del aro.

${\displaystyle \frac{d\omega }{dt}=-\frac{\mu g}{2\pi R^2}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\left(\frac{R(\omega R-v\text{sin}\theta )}{\sqrt{v^2+{\omega }^2{R}^2-2v\omega R\text{sin}\theta }}\right)d\theta }}$

Para calcular la posición x y la velocidad v del centro del aro, el ángulo girado φ, y velocidad angular ω de rotación en función del tiempo t, se ha de resolver, empleando procedimientos numéricos, un sistema de dos ecuaciones diferenciales de segundo orden.

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}=-\frac{\mu g}{2\pi }f(v,\omega )v=\frac{dx}{dt}\\ \frac{d^2\varphi }{d{t}^2}=-\frac{\mu g}{2\pi R^2}g(v,\omega )\omega =\frac{d\varphi }{dt}\end{array}}$

Previamente, hemos de obtener los valores de las funciones f(v, ω) y g(v, ω) calculando numéricamente las dos integrales para cada valor de v y ω.

Casos particulares

• Solamente hay movimiento de traslación, ω=0

${\displaystyle \begin{array}{l}\frac{dv}{dt}=-\frac{\mu g}{2\pi }{\displaystyle \underset{0}{\overset{2\pi }{\int }}d\theta }=-\mu g\\ \frac{d\omega }{dt}=-\frac{\mu g}{2\pi }{\displaystyle \underset{0}{\overset{2\pi }{\int }}-R\text{sin}\theta ·d\theta }=0\end{array}}$

El centro del aro sigue una trayectoria rectilínea. Parte con velocidad inicial v₀, va disminuyendo con el tiempo hasta que se para.

${\displaystyle v=v_0-\mu gtx=v_{0}t-\frac{1}{2}\mu g{t}^2}$

El tiempo t que tarda en parase y su desplazamiento x son, respectivamente

${\displaystyle t=\frac{v_0}{\mu g}x=\frac{1}{2}\frac{v_0^2}{\mu g}}$

• Solamente hay movimiento de rotación, v=0

${\displaystyle \begin{array}{l}\frac{dv}{dt}=-\frac{\mu g}{2\pi }{\displaystyle \underset{0}{\overset{2\pi }{\int }}-\text{sin}\theta ·d\theta }=0\\ \frac{d\omega }{dt}=-\frac{\mu g}{2\pi R^2}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{\omega R^2}{\omega R}d\theta }=\frac{-\mu g}{R}\end{array}}$

El centro del aro permanece en reposo. Gira alrededor del eje perpendicular al plano del aro y que pasa por su centro, con velocidad inicial ω₀, que va disminuyendo con el tiempo, hasta que se para.

${\displaystyle \omega ={\omega }_0-\frac{\mu g}{R}t\varphi ={\omega }_{0}t-\frac{1}{2}\frac{\mu g}{R}{t}^2}$

El tiempo t que tarda en parase y su desplazamiento angular φ son, respectivamente

${\displaystyle t=\frac{{\omega }_{0}R}{\mu g}\varphi =\frac{1}{2}\frac{{\omega }_0^2{R}^2}{\mu g}}$

Ecuaciones del movimiento del disco

Sea un disco de masa m_d y de radio R. El centro del disco se mueve con velocidad v, y gira alrededor de un eje perpendicular al plano del disco y que pasa por el centro, con velocidad angular ω.

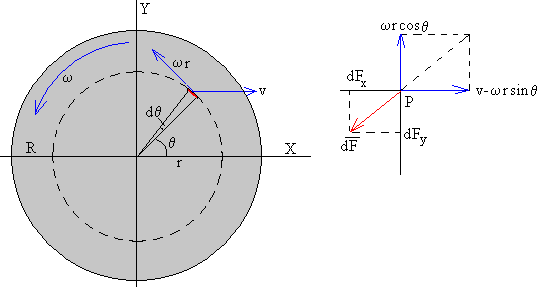
El vector velocidad de un punto P que dista r del centro y cuya posición angular es θ, es

v_p=(v-ωrsinθ)i+(ωrcosθ)j

La fuerza de rozamiento dF que actúa sobre el elemento de masa dm se opone al movimiento de dicho elemento, su dirección es la misma que la velocidad v, y de sentido contrario.

${\displaystyle dF=-\mu ·dm·g\frac{v_p}{v_p}}$

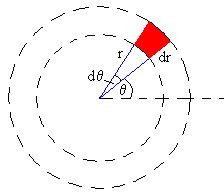Si md es la masa del disco, la masa dm contenida en el elemento de área (r·dθ)dr, es dm=md·r·dθ·dr/(πR2)

Resultante de las fuerzas que actúan sobre el disco

Las componentes del vector dF sobre dicho elemento son

${\displaystyle \begin{array}{l}d{F}_x=-\frac{m_d}{\pi R^2}\mu g\frac{v-\omega r\text{sin}\theta }{\sqrt{v^2+{\omega }^2{r}^2-2v\omega r\text{sin}\theta }}rd\theta ·dr\\ d{F}_y=-\frac{m_d}{\pi R^2}\mu g\frac{\omega r\text{cos}\theta }{\sqrt{v^2+{\omega }^2{r}^2-2v\omega r\text{sin}\theta }}rd\theta ·dr\end{array}}$

Las componentes de la fuerza resultante sobre el disco son

${\displaystyle \begin{array}{l}{F}_x=-\frac{m_d}{\pi R^2}\mu g{\displaystyle \underset{0}{\overset{2\pi }{\int }}d\theta {\displaystyle \underset{0}{\overset{R}{\int }}\frac{v-\omega r\text{sin}\theta }{\sqrt{v^2+{\omega }^2{r}^2-2v\omega r\text{sin}\theta }}rdr}}\\ F_y=-\frac{m_d}{\pi R^2}\mu g{\displaystyle \underset{0}{\overset{2\pi }{\int }}d\theta {\displaystyle \underset{0}{\overset{R}{\int }}\frac{\omega r\text{cos}\theta }{\sqrt{v^2+{\omega }^2{r}^2-2v\omega r\text{sin}\theta }}rdr}}\end{array}}$

Por simetría F_y=0.

Ecuación del movimiento del centro de masas del disco

${\displaystyle \begin{array}{l}{m}_a\frac{dv}{dt}=F_x\\ \frac{dv}{dt}=-\frac{\mu g}{\pi R^2}{\displaystyle \underset{0}{\overset{2\pi }{\int }}d\theta {\displaystyle \underset{0}{\overset{R}{\int }}\frac{v-\omega r\text{sin}\theta }{\sqrt{v^2+{\omega }^2{r}^2-2v\omega r\text{sin}\theta }}rdr}}\end{array}}$

Momento de las fuerzas sobre los elementos del disco, respecto de su centro.

${\displaystyle \begin{array}{l}dM=r\times dF=r\times \left(-\mu ·dm·g\frac{v}{v}\right)=-\mu ·dm·g\left(r\cos \theta i+r\text{sin}\theta j\right)\times \\ \left(\frac{v-\omega r\text{sin}\theta }{\sqrt{v^2+{\omega }^2{r}^2-2v\omega r\text{sin}\theta }}i+\frac{\omega r\text{cos}\theta }{\sqrt{v^2+{\omega }^2{r}^2-2v\omega r\text{sin}\theta }}j\right)=\\ -\mu ·dm·g\left(\frac{\omega r^2{\text{cos}}^{\text{2}}\theta }{\sqrt{v^2+{\omega }^2{r}^2-2v\omega r\text{sin}\theta }}-\frac{R\text{sen}\theta (v-\omega r\text{sin}\theta )}{\sqrt{v^2+{\omega }^2{r}^2-2v\omega r\text{sin}\theta }}\right)k=\\ -\frac{m_d}{\pi R^2}\mu g\left(\frac{r(\omega r-v\text{sin}\theta )}{\sqrt{v^2+{\omega }^2{r}^2-2v\omega r\text{sin}\theta }}\right)r·d\theta ·dr·k\end{array}}$

El momento total de las fuerzas sobre los elementos del disco, respecto del centro es

${\displaystyle M=-\frac{m_d}{\pi R^2}\mu g{\displaystyle \underset{0}{\overset{2\pi }{\int }}d\theta {\displaystyle \underset{0}{\overset{R}{\int }}\left(\frac{r^2(\omega r-v\text{sin}\theta )}{\sqrt{v^2+{\omega }^2{r}^2-2v\omega r\text{sin}\theta }}\right)}}dr}$

Ecuación de la dinámica de rotación I(dω/dt)=M. Donde I=(1/2)m_d·R² es el momento de inercia del disco.

${\displaystyle \frac{d\omega }{dt}=-\frac{2\mu g}{\pi R^4}{\displaystyle \underset{0}{\overset{2\pi }{\int }}d\theta {\displaystyle \underset{0}{\overset{R}{\int }}\left(\frac{r^2(\omega r-v\text{sin}\theta )}{\sqrt{v^2+{\omega }^2{r}^2-2v\omega r\text{sin}\theta }}\right)}}dr}$

Para calcular la posición x y la velocidad v del centro del disco, el ángulo girado φ, y velocidad angular ω de rotación en función del tiempo t, se ha de resolver, empleando procedimientos numéricos, un sistema de dos ecuaciones diferenciales de segundo orden.

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}=-\frac{\mu g}{\pi R^2}f(v,\omega )v=\frac{dx}{dt}\\ \frac{d^2\varphi }{d{t}^2}=-\frac{2\mu g}{\pi R^4}g(v,\omega )\omega =\frac{d\varphi }{dt}\end{array}}$

Previamente, hemos de obtener los valores de las funciones f(v, ω) y g(v, ω) calculando numéricamente las dos integrales dobles para cada valor de v y ω.

Casos particulares

• Solamente hay movimiento de traslación, ω=0

${\displaystyle \begin{array}{l}\frac{dv}{dt}=-\frac{\mu g}{\pi R^2}{\displaystyle \underset{0}{\overset{2\pi }{\int }}d\theta {\displaystyle \underset{0}{\overset{R}{\int }}r·dr}}=-\mu g\\ \frac{d\omega }{dt}=-\frac{2\mu g}{\pi R^4}{\displaystyle \underset{0}{\overset{2\pi }{\int }}d\theta {\displaystyle \underset{0}{\overset{R}{\int }}{r}^2(-\text{sin}\theta )}dr}=0\end{array}}$

El centro del disco sigue una trayectoria rectilínea. Parte con velocidad inicial v₀, va disminuyendo con el tiempo, hasta que se para.

${\displaystyle v=v_0-\mu gtx=v_{0}t-\frac{1}{2}\mu g{t}^2}$

El tiempo t que tarda en parase y su desplazamiento x son, respectivamente

${\displaystyle t=\frac{v_0}{\mu g}x=\frac{1}{2}\frac{v_0^2}{\mu g}}$

• Solamente hay movimiento de rotación, v=0

${\displaystyle \begin{array}{l}\frac{dv}{dt}=-\frac{\mu g}{2\pi }{\displaystyle \underset{0}{\overset{2\pi }{\int }}d\theta {\displaystyle \underset{0}{\overset{R}{\int }}-r\text{sin}\theta ·dr}}=0\\ \frac{d\omega }{dt}=-\frac{2\mu g}{\pi R^4}{\displaystyle \underset{0}{\overset{2\pi }{\int }}d\theta {\displaystyle \underset{0}{\overset{R}{\int }}{r}^{2}dr}=\frac{-4\mu g}{3R}}\end{array}}$

El centro del disco permanece en reposo. Gira alrededor del eje perpendicular al plano del disco y que pasa por su centro, con velocidad inicial ω₀, que va disminuyendo con el tiempo, hasta que se para.

${\displaystyle \omega ={\omega }_0-\frac{4\mu g}{3R}t\varphi ={\omega }_{0}t-\frac{1}{2}\frac{4\mu g}{3R}{t}^2}$

El tiempo t que tarda en parase y su desplazamiento angular φ son, respectivamente

${\displaystyle t=\frac{3{\omega }_{0}R}{4\mu g}\varphi =\frac{3}{8}\frac{{\omega }_0^2{R}^2}{\mu g}}$

Ejemplo

• Coeficiente de rozamiento μ=0.3 entre el aro o disco y el plano horizontal sobre el que deslizan.

• El radio del aro o del disco es R=1 m.

Aro

• Velocidad inicial de traslación del c.m. v₀=5 m/s

• Velocidad inicial de rotación ω₀=0

La aceleración constante es – μ·g=-2.94 m/s²

El tiempo que tarda en parase es t=5/2.94=1.70 s

El desplazamiento del centro del aro en este tiempo es x=4.25 m

Disco

Para el disco se obtienen los mismos resultados

Aro

• Velocidad inicial de traslación del c.m.,v₀=0

• Velocidad inicial de rotación, ω₀=1 rad/s

La aceleración angular constante es – μ·g/R=-2.94 m/s²

El tiempo que tarda en parase es t=1.0/2.94=0.34 s

El ángulo girado por el aro en este tiempo es φ=0.17 rad

Disco

La aceleración angular constante es – 4μ·g/(3R)=-3.92 m/s²

El tiempo que tarda en parase es t=1/3.92=0.26 s

El ángulo girado por el disco en este tiempo es φ=0.13 rad

Aro

• Velocidad inicial de traslación del c.m., v₀=5 m/s

• Velocidad inicial de rotación, ω₀=1 rad/s

El tiempo que tarda en parase es t=1.78 s

El ángulo girado por el aro en este tiempo es φ=1.15 rad

El desplazamiento del centro del aro en este tiempo es x=4.34 m

• Velocidad inicial de traslación del c.m., v₀=1 m/s

• Velocidad inicial de rotación, ω₀=5 rad/s

El tiempo que tarda en parase es t=1.78 s

El ángulo girado por el aro en este tiempo es φ=4.34 rad

El desplazamiento del centro del aro en este tiempo es x=1.15 m

Actividades

Se introduce

• El cuerpo que desliza: aro o disco, activando el botón de radio correspondiente

• La velocidad inicial de traslación v₀ del c.m., en el control de edición titulado V. traslación

• La velocidad inicial rotación ω₀, en el control de edición titulado V. rotación

• El coeficiente de rozamiento μ, actuando en la barra de desplazamiento titulada Coef. rozamiento.

• El radio del aro o del disco se ha fijado en R=1 m

Se pulsa el botón titulado Empieza

Cuando la velocidad inicial v₀ de traslación del c.m. y la velocidad inicial de rotación ω₀, son distintas de cero, el programa interactivo realiza un cálculo numérico intensivo, que aunque ha sido verificado, no está libre de inexactitudes. En el caso del disco, las operaciones a realizar son más de cuatro veces las que se efectúan con el aro, por lo que la animación puede resultar deficiente en los ordenadores con menor capacidad de procesamiento.

stokesApplet aparecerá en un explorador compatible con JDK 1.1.

Referencias

Voyenli K., Eriksen E. On the motion of an ice puck. Am. J. Phys. 53 (12) December 1985, pp. 1149-1153

Curso Interactivo de Física en Internet © Ángel Franco García