Desplazando el plano sobre el se apoya un cuerpo redondo.
Una experiencia sencilla consiste en poner una botella o cualquier objeto de forma redonda sobre un mantel encima de una mesa y a continuación, se tira del mantel. El cuerpo redondo se desplaza en la dirección del mantel mientras gira en sentido contrario. La fuerza de fricción entre el mantel y el cuerpo produce ambos movimientos.
Hay que tener cuidado en la forma en la que tiramos: Si tiramos del mantel muy despacio el objeto redondo puede trasladarse sin girar. Si tiramos demasiado fuerte puede deslizar sobre el mantel sin girar.
Descripción
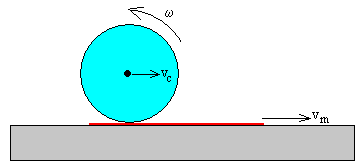
En la figura, se representa un cuerpo redondo de masa m y radio R que rueda sin deslizar sobre un mantel que se desplaza hacia la derecha con velocidad constante vm. Vamos a calcular la velocidad del centro de masa de dicho cuerpo vc respecto de la mesa y su velocidad angular ω de rotación.
Dinámica
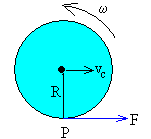La fuerza F que ejerce el mantel sobre el cuerpo
redondo actúa en el punto de contacto P. Las otras dos fuerzas: el peso y la
reacción del plano horizontal no contribuyen al movimiento.
Las ecuaciones del movimiento son:
-
Movimiento de traslación del centro de masas
F=m·ac
-
Movimiento de rotación alrededor de un eje que pasa por el c.m.
F·R=Ic·α
donde Ic=kmR2, siendo k=1 para un aro, k=1/2 para un cilindro y k=2/5 para una esfera.
Las dos ecuaciones nos permiten relacionar ambas aceleraciones ac=k·Rα
La misma relación se establece entre las velocidades vc de traslación del c.m. y la velocidad angular de rotación alrededor de un eje que pase por el c.m.
vc=k·Rω
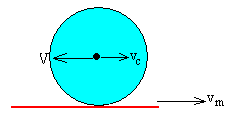Si el cuerpo rueda
sin deslizar sobre el mantel, la velocidad V del c.m. respecto
del mantel será V=ωR y estará dirigida hacia la izquierda ya que la
velocidad angular de rotación ω es de sentido contrario a las agujas del reloj. Teniendo en cuenta el
signo, la relación entre ambas velocidades será vc =-kV
Si la velocidad del mantel es vm se cumplirá que V=vc-vm
Conocida la velocidad vm del mantel calculamos la velocidad vc del c.m. del cuerpo respecto de la mesa
y la velocidad relativa V del cuerpo respecto del mantel
Si d es la distancia inicial que hay entre el punto P de contacto entre el cuerpo y el mantel y su borde izquierdo. El tiempo que emplea el cilindro en abandonarlo es t=d/|V|. En ese mismo tiempo, el c.m. del cilindro ha recorrido hacia la derecha una distancia x=vc·t=k·d.
Momento angular
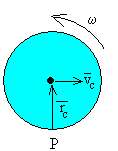La fuerza exterior F que hace moverse al
cilindro está aplicada en el punto P. El momento de dicha fuerza es cero.
Por lo que el momento angular respecto de P debe de ser constante.
Para un sistema de partículas la relación entre el momento angular respecto a un eje que pasa por el c.m. y el momento angular respecto de un eje instantáneo que pasa por P es
L=Lcm+m·rcm × vcm
Los dos momentos angulares tienen la misma dirección (perpendicular al plano del dibujo) y sentidos opuestos
L=Icω-mRvc=0
Escribiendo Ic=kmR2, obtenemos de nuevo, la misma relación entre la velocidad de traslación del c.m. y la velocidad de rotación ω.
vc=kRω
Cuando el cuerpo redondo abandona el mantel, no puede moverse ni a la izquierda ni a la derecha, queda completamente en reposo, ya que de otro modo el momento angular dejaría de ser nulo.
Actividades
Se introduce
- La velocidad vm del mantel en el control de edición titulado Velocidad
- Se elige el tipo de cuerpo que rueda, un cilindro, aro o esfera en el control de selección titulado Cuerpo.
- El radio R y la masa m del cuerpo redondo se han fijado en una unidad.
Se pulsa el botón titulado Empieza
Se observa el movimiento de traslación del c.m. del cuerpo respecto de la mesa hacia la derecha mientras rueda hacia la izquierda sobre el mantel.
Podemos relacionar el desplazamiento x del del c.m. respecto de la mesa con el desplazamiento del cuerpo sobre el mantel d para cada uno de los cuerpos.
Observamos que cuando abandona el mantel, el cuerpo permanece en reposo.
Referencias
Ferguson J. Pulling the rug from under round objects. The Physics Teacher vol 39, April 2001, pp. 224-225.