Problemas ciclos térmicos

Ciclos térmicos

Problema 1

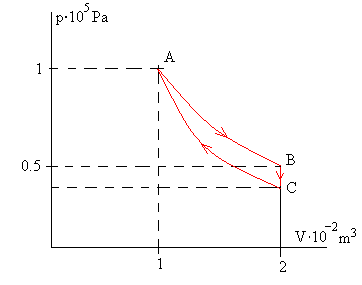
1.-Consideremos helio (gas perfecto monoatómico c_v=3R/2) en el estado inicial A: p_A=10⁵ Pa, V_A=10^-2 m³ y T_A=300 K. Se llevan a cabo las siguientes transformaciones:

A-B: Transformación isoterma reversible siendo V_B=2 10^-2 m³

B-C: Transformación isócora (V=cte) reversible siendo T_C=189 K

C-A: Transformación adiabática reversible, que devuelve al gas a sus condiciones iniciales.

a) Determinar el número de moles de helio, confeccionar una tabla en la que aparezcan los valores p, V y T en los tres estados A, B y C, y dibujar el ciclo en el diagrama p-V.

b) Calcular, en unidades del sistema internacional, de forma directa (siempre que sea posible) el trabajo W, el calor Q, y la variación de energía interna ΔU, del gas para cada uno de los procesos.

c) Determinar el rendimiento de este ciclo como motor térmico

Dato: R=8.314 J/(mol·K)

Solución

Vértice A: p_AV_A=nRT_A

nR= 10 5 · 10 −2 300 = 10 3

Transformación isoterma: p_AV_A= p_BV_B, p_B=0.5·10⁵ Pa

Transformación isócora: V_B=V_C.

Vértice C: p_CV_C=nRT_C, p_C=0.315·10⁵ Pa

Vértice	p (Pa)	V (m³)	T (K)
A	10⁵	10^-2	300
B	0.5·10⁵	2·10^-2	300
C	0.315·10⁵	2·10^-2	189

Índice adiabático

γ= c p c v = 3 2 R+R 3 2 R = 5 3

A→B, proceso isotermo

ΔU_AB=0

W= ∫ A B p·dV = ∫ A B nRT V ·dV =nRTln⁡ V B V A W AB = 10 3 ·300·ln⁡ 2· 10 −2 10 −2 =1000ln⁡2 J Q AB = W AB =1000ln⁡2 J

B→C, proceso isócoro

Δ U BC =n c v ( T C − T B )=n 3 2 R(189−300)= 10 3 3 2 (−111)=−555 J

W_BC=0

Q_BC= ΔU_BC=-555 J

C→A, proceso adiabático

Q_CA=0

Δ U CA =n c v ( T A − T C )=n 3 2 R(300−189)= 10 3 3 2 111=555 J

W_CA=- ΔU_CA=-555 J

Calculo del trabajo de forma directa

Ecuación de una adiabática

p V γ =cte= p C V C γ = p A V A γ W CA = ∫ C A p·dV = ∫ C A cte V γ ·dV = cte −γ+1 ( V A −γ+1 − V C −γ+1 )= 1 −γ+1 ( p A V A γ · V A −γ+1 − p C V C γ · V C −γ+1 )= 1 −γ+1 ( p A V A − p C V C )= 1 − 5 3 +1 ( 10 5 · 10 −2 −0.315· 10 5 ·2· 10 −2 )=−555 J

Ciclo completo

Proceso	ΔU (J)	Q (J)	W(J)
A→B	0	693	693
B→C	-555	-555	0
C→A	555	0	-555
Total	0		138

Calor absorbido, Q_abs=693 J
Calor cedido, Q_ced=-555
Trabajo realizado, W=138 J

Se cumple que, Q_abs+Q_ced≈W

Rendimiento

η= W Q abs = 138 693 =0.20 (20%)

Problema 2

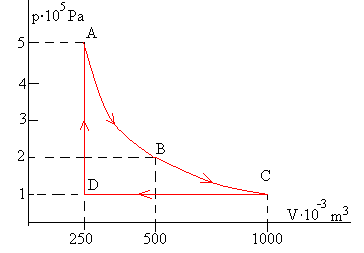
Diez moles de un gas diatómico (c_v=5R/2) se encuentran inicialmente a una presión de p_A = 5·10⁵ Pa y ocupando un volumen de V_A = 249·10^-3 m³. Se expande adiabáticamente (proceso AB) hasta ocupar un volumen V_B = 479·10^-3 m³. A continuación el gas experimenta una transformación isoterma (proceso BC) hasta una presión p_C = 10⁵ Pa. Posteriormente se comprime isobáricamente (proceso CD) hasta un volumen V_D = V_A = 249·10^-3 m³. Por último, experimenta una transformación a volumen constante (proceso DA) que le devuelve al estado inicial.

Representar gráficamente este ciclo en un diagrama p-V.
Calcular el valor de las variables termodinámicas desconocidas en los vértices A, B, C y D.
Hallar el calor, el trabajo, la variación de energía interna, en Joules, de forma directa y/o empleando el Primer Principio, en cada etapa del ciclo.
Calcular el rendimiento.

R= 0.082 atm·l/(mol·K) = 8.314 J/(mol·K) ; 1 cal = 4.186 J; 1 atm = 1.013 10⁵ Pa

Solución

Índice adiabático

γ= c p c v = 5 2 R+R 5 2 R = 7 5

Vértice A. p_A·V_A=nRT_A, T_A=1497.5 K

A→B, proceso adiabático. p A V A γ = p B V B γ p B =2· 10 5 Pa

Vértice B. p_B·V_B=nRT_B, T_B=1152.7 K

B→C, proceso isotérmico. . p_B·V_B= p_C·V_C , V_C =958.3·10^-3 m³

Vértice D. p_D·V_D=nRT_D, T_D=299. 5 K

Vértice	p (Pa)	V (m³)	T (K)
A	5·10⁵	249·10^-3	1497.5
B	2·10⁵	479·10^-3	1152.7
C	1·10⁵	958.3·10^-3	1152.7
D	1·10⁵	249·10^-3	299.5

A→B, proceso adiabático

Q_AB=0

Δ U AB =n c v ( T B − T A )=10 5 2 8.314(1152.7−1497.5)=−71 667 J

W_AB=- ΔU_AB=-71 667 J

Calculo del trabajo de forma directa

p V γ =cte= p A V A γ = p B V B γ W AB = ∫ A B p·dV = ∫ A B cte V γ ·dV = cte −γ+1 ( V B −γ+1 − V A −γ+1 )= 1 −γ+1 ( p B V B γ · V B −γ+1 − p A V A γ · V A −γ+1 )= 1 −γ+1 ( p B V B − p A V A )= 1 − 7 5 +1 ( 2· 10 5 ·479· 10 −3 −5· 10 5 ·249· 10 −3 )=71 750 J

Como vemos, W_AB≈- ΔU_AB

B→C, proceso isotermo

ΔU_BC=0

W= ∫ B C p·dV = ∫ B C nRT V ·dV =nRTln⁡ V C V B W BC =10·8.314·1152.7·ln⁡ 958· 10 −3 479· 10 −3 =66 458 J Q BC = W BC =66 458 J

C→D, proceso isóbaro

Δ U CD =n c v ( T D − T C )=10 5 2 8.314(299.5−1152.7)=−177 338 J Q CD =n c p ( T D − T C )=10 7 2 8.314(299.5−1152.7)=−248 273 J W CD =p( V D − V C )= 10 5 ( 249· 10 −3 −958· 10 −3 )=−70 930 J

Comprobación, ΔU≈Q-W

D→A, proceso isócoro

Δ U DA =n c v ( T A − T D )=10 5 2 8.314(1497.5−299.5)=249 004 J

W_DA=0

Q_DA= ΔU_DA= 249 004 J

Ciclo completo

Proceso	ΔU (J)	Q (J)	W(J)
A→B	-71 667	0	71 667
B→C	0	66 458	66 458
C→D	-177 338	-248 273	-70 930
D→A	249 004	249 004	0
Total	0		67 278

Calor absorbido, Q_abs=315 462 J
Calor cedido, Q_ced=-248 273
Trabajo realizado, W=67 278 J

Se cumple que, Q_abs+Q_ced≈W

Rendimiento

η= W Q abs = 67 278 315 462 =0.21 (21%)

Problema 3

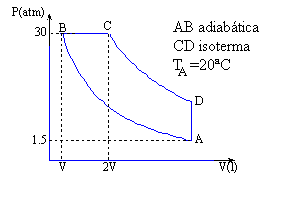Una máquina térmica trabaja con 3 moles de un gas monoatómico, describiendo el ciclo reversible ABCD de la figura. Sabiendo que V_C = 2 V_B:

Calcular el valor de las variables termodinámicas desconocidas en cada vértice.
Deducir las expresiones del trabajo en cada etapa del ciclo.
Calcular de forma directa en cada etapa del ciclo (siempre que sea posible), el trabajo, el calor, la variación de energía interna y la variación de entropía
El rendimiento del ciclo.

R=0.082 atm·l/(mol·K) = J/(mol·K); 1cal=4.186 J; 1atm=1.013·10⁵Pa, c_v=3R/2

Solución

Índice adiabático

γ= c p c v = 3 2 R+R 3 2 R = 5 3

Vértice A. p_A·V_A=nRT_A, 1.5·V_A=3·0.082·293, V_A=48.05 l

A→B, proceso adiabático. p A V A γ = p B V B γ 1.5· 48.05 5/3 =30· V B 5/3 V B =7.96 l

Vértice B. p_B·V_B=nRT_B, T_B=971.1 K

Vértice C. p_B·2V_B=nRT_C, T_C=1942.3 K

C→D, proceso isotérmico. . p_C·V_C= p_D·V_D , p_D =9.95 atm

Vértice	p (atm)	V (l)	T (K)
A	1.5	48.05	293
B	30	7.96	971.1
C	30	15.93	1942.3
D	9.95	48.05	1942.3

A→B, proceso adiabático

Q_AB=0

Δ U AB =n c v ( T B − T A )=3 3 2 0.082(971.1−293)=−250.2 atm·l

W_AB=- ΔU_AB=--250.2 atm·l

Calculo del trabajo de forma directa

p V γ =cte= p A V A γ = p B V B γ W AB = ∫ A B p·dV = ∫ A B cte V γ ·dV = cte −γ+1 ( V B −γ+1 − V A −γ+1 )= 1 −γ+1 ( p B V B γ · V B −γ+1 − p A V A γ · V A −γ+1 )= 1 −γ+1 ( p B V B − p A V A )= 1 − 5 3 +1 ( 1.5·48.05−30·7.96 )=250.1 atm·l

Como vemos, W_AB≈- ΔU_AB

ΔS_AB=0

B→C, proceso isóbaro

Δ U BC =n c v ( T C − T B )=3 3 2 0.082(1942.3−971.1)=358.4 atm·l Q BC =n c p ( T C − T B )=3 5 2 0.082(1942.3−971.1)=597.3 atm·l W BC =p( V C − V B )=30( 15.93−7.96 )=239.1 atm·l Δ S BC = ∫ B C n c p dT T =n c P ln⁡ T C T B =3 5 2 0.082ln⁡ 1942.3 971.1 =0.43 atm·l/K

Comprobación, ΔU≈Q-W

C→D, proceso isotermo

ΔU_CD=0

W= ∫ C D p·dV = ∫ C D nRT V ·dV =nRTln⁡ V D V C ≠ W CD =3·0.082·1942.3·ln⁡ 48.05 15.93 =527.5 atm·l Q CD = W CD =527.5 atm·l Δ S CD = Q CD T D = 527.5 1942.3 =0.27 atm·l/K

D→A, proceso isócoro

Δ U DA =n c v ( T A − T D )=3 3 2 0.082(293−1942.3)=−608.6 atm·l W DA =0 Q DA =Δ U DA =−608.6 atm·l Δ S DA = ∫ D A n c v dT T =n c v ln⁡ T A T D =3 3 2 0.082ln⁡ 293 1942.3 =−0.70 atm·l/K

Ciclo completo

Proceso	ΔU (atm·l)	Q (atm·l)	W(atm·l)	ΔS (atm·l/K)
A→B	250.2	0	-250.2	0
B→C	358.4	597.3	239.1	0.43
C→D	0	527.5	527.5	0.27
D→A	-608.6	-608.6	0	-0.70
Total	0		516.4	0

Calor absorbido, Q_abs=1124.8 atm·l
Calor cedido, Q_ced=-608.6 atm·l
Trabajo realizado, W=516.4 atm·l

Se cumple que, Q_abs+Q_ced≈W

Rendimiento

η= W Q abs = 516.4 608.4 =0.46 (46%)

Problema 4

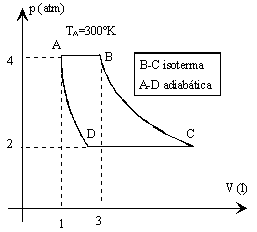El ciclo de la figura que describe un gas ideal monoatómico

Calcular el valor de las variables termodinámicas desconocidas en los vértices A, B y C.
Hallar de forma directa el trabajo en cada etapa.
El calor, la variación de energía interna y la variación de entropía en cada etapa del ciclo. (Expresar los resultados en Joules).
Hallar el rendimiento del ciclo.

R=0.082 atm·l/(K·mol) 1 cal= 4.186 J. 1 atm = 1.013·10⁵ Pa

Solución

Índice adiabático

γ= c p c v = 3 2 R+R 3 2 R = 5 3

Vértice A. p_A·V_A=nRT_A, nR=4/300=1/75

D→A, proceso adiabático.

p A V A γ = p D V D γ 4· 1 5/3 =2· V D 5/3 V D =1.52 l p D V D =nR T D 2·1.52= 1 75 T D T D =227.3 K

Vértice B. p_B·V_B=nRT_B, T_B=900 K

Vértice C. p_C·V_C=nRT_B, V_C=6 l

C→D, proceso isotérmico. . p_C·V_C= p_D·V_D , p_D =9.95 atm

Vértice	p (atm)	V (l)	T (K)
A	4	1	300
B	4	3	900
C	2	6	900
D	2	1.52	227.3

A→B, proceso isóbaro

Δ U AB =n c v ( T B − T A )= 3 2 1 75 (900−300)=12 atm·l Q AB =n c p ( T C − T B )= 5 2 1 75 (900−300)=20 atm·l W AB = p A ( V B − V A )=4( 3−1 )=8 atm·l Δ S AB = ∫ A B n c p dT T =n c P ln⁡ T B T A = 5 2 1 75 ln⁡ 900 300 =0.037 atm·l/K

Comprobación, ΔU≈Q-W

B→C, proceso isotermo

ΔU_BC=0

W= ∫ B C p·dV = ∫ B C nRT V ·dV =nRTln⁡ V C V B W BC = 1 75 ·900ln⁡ 6 3 =8.32 atm·l Q BC = W BC =8.32 atm·l Δ S BC = Q BC T B = 8.32 900 =0.0094 atm·l/K

C→D, proceso isóbaro

Δ U CD =n c v ( T D − T C )= 3 2 1 75 (227.3−900)=−13.45 atm·l Q CD =n c p ( T D − T C )= 5 2 1 75 (227.3−900)=−22.41 atm·l W CD = p C ( V D − V C )=2( 1.52−6 )=−8.96 atm·l Δ S CD = ∫ C D n c p dT T =n c P ln⁡ T D T C = 5 2 1 75 ln⁡ 227.3 900 =−0.046 atm·l/K

Comprobación, ΔU≈Q-W

D→A, proceso adiabático

Q_DA=0

Δ U DA =n c v ( T A − T D )= 3 2 1 75 (300−227.3)=1.45 atm·l

W_DA=-ΔU_DA=1.45 atm·l

Calculo del trabajo de forma directa

p V γ =cte= p A V A γ = p D V D γ W DA = ∫ D A p·dV = ∫ D A cte V γ ·dV = cte −γ+1 ( V A −γ+1 − V D −γ+1 )= 1 −γ+1 ( p A V A γ · V A −γ+1 − p D V D γ · V D −γ+1 )= 1 −γ+1 ( p A V A − p D V D )= 1 − 5 3 +1 ( 4·1−2·1.52 )=−1.45 atm·l

Como vemos, W_DA≈- ΔU_DA

ΔS_DA=0

Factor de conversión. 1 atm·l=1.013·10⁵·10^-3=101.3 J

Ciclo completo

Proceso	ΔU (J)	Q (J)	W(J)	ΔS(J/K)
A→B	1216	2026	810	3.71
B→C	0	843	843	0.94
C→D	-1362	-2269	-908	-4.65
D→A	147	0	-147	0
Total	0		598	0

Calor absorbido, Q_abs=2869 J
Calor cedido, Q_ced=-2269 J
Trabajo realizado, W=598 J

Se cumple que, Q_abs+Q_ced≈W

Rendimiento

η= W Q abs = 598 2869 =0.21 (21%)