

Conservación del momento angular
Problema 1
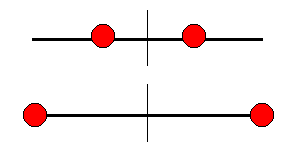 Dos esferas iguales de masas 6 kg y 20 cm de radio están montadas como se
indica en la figura, y pueden deslizar a lo largo de una varilla delgada de 3 kg
de masa y 2 m de longitud. El conjunto gira libremente con una velocidad
angular de 120 rpm respecto a un eje vertical que pasa por el centro del
sistema.
Dos esferas iguales de masas 6 kg y 20 cm de radio están montadas como se
indica en la figura, y pueden deslizar a lo largo de una varilla delgada de 3 kg
de masa y 2 m de longitud. El conjunto gira libremente con una velocidad
angular de 120 rpm respecto a un eje vertical que pasa por el centro del
sistema.
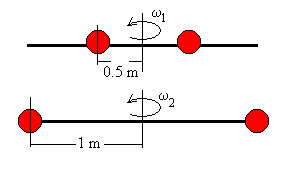
Inicialmente los centros de las esferas se encuentran fijos a 0.5 m del eje
de giro. Se sueltan las esferas y las esferas deslizan por la barra hasta que
salen por los extremos. Calcular:
- La velocidad angular de rotación cuando los centros de las
esferas se encuentran en los extremos de la varilla.
- Hallar la energía cinética del sistema en los dos casos.
 Solución
Solución
Conservación del momento angular
I
1
=
1
12
3·
2
2
+2(
2
5
6·
0.2
2
+6·
0.5
2
)
ω
1
=
120·2π
60
=4π rad/s
I
2
=
1
12
3·
2
2
+2(
2
5
6·
0.2
2
+6·
1
2
)
I
1
ω
1
=
I
2
ω
2
ω
2
=1.27π rad/s
Variación de la energía cinética
E
k1
=
1
2
I
1
ω
1
2
=330.99 J
E
k2
=
1
2
I
2
ω
2
2
=105.20 J
Problema 2
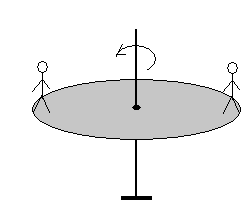 |
Dos niños de 25 kg de masa cada uno están situados en el
borde de un disco de 2.6 m de diámetro y 10 kg de masa. El disco gira a razón
de 5 rpm respecto del eje perpendicular al disco y que pasa por su centro.
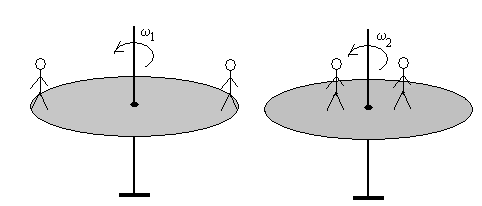
- ¿Cuál será la velocidad angular del conjunto si cada niño se desplaza 60
cm hacia el centro del disco?.
- Calcular la variación de energía cinética de rotación del sistema, y
explica la causa del incremento de energía.
|
 Solución
Solución
Conservación del momento angular
I
1
=
1
2
10·
1.3
2
+2(
25·
1.3
2
)
ω
1
=
5·2π
60
=
π
6
rad/s
I
2
=
1
2
10·
1.3
2
+2(
25·
0.7
2
)
I
1
ω
1
=
I
2
ω
2
ω
2
=1.48 rad/s
Variación de la energía cinética
ΔE=
E
k2
−
E
k1
=
1
2
I
2
ω
2
2
−
1
2
I
1
ω
1
2
=27.2 J
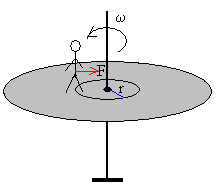 |
La fuerza sobre un niño para que describa un movimiento circular de radio r es F=mω2r, cuando la plataforma gira con velocidad angular ω. El trabajo de la fuerza F cuando el niño pasa de la
posición inicial (en el borde) a la posición final (hacia el centro) incrementa
la energía cinética de rotación. |
Problema 3
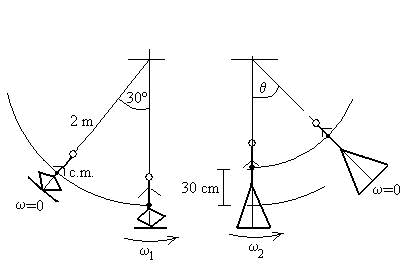
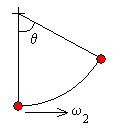
Un niño de 25 kg está agachado sobre la tabla de un
columpio desviado 30º de la vertical. La distancia entre el punto de suspensión
y el c.m. del niño es 2 m.
- Calcular la velocidad angular ω1 con
la que llega a la posición de equilibrio.
- En esta posición, el niño se levanta
rápidamente quedándose de pié sobre el columpio, con lo que eleva su centro de
masa 30 cm. Como consecuencia su velocidad angular se incrementa.
Calcular la velocidad angular ω2,
- Calcula la máxima desviación θ, del niño cuando
está de pié sobre el columpio.
- ¿Cuánto vale la tensión de la cuerda cuando pasa por la posición θ/2?.
 Solución
Solución
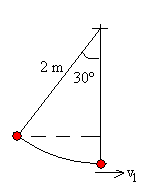 |
Conservación de la energía
25
·
9.8
(
2
−
2
·
cos
30
)
=
1
2
25
v
1
2
v
1
=
2.29
m/s
ω
1
=
1.15
rad/s
|
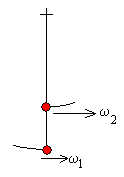 |
Conservación del momento angular
25
·
2
2
ω
1
=
25
·
1.7
2
ω
2
ω
2
=
1.60
rad/s
|
 |
Conservación de la energía
1
2
25
·
(
1.7
·
ω
2
)
2
=
25
·
9.8
·
(
1.7
−
1.7
·
cos
θ
)
θ
=
38.6
º
|
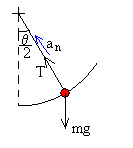 Tensión de la cuerda para θ/2
Tensión de la cuerda para θ/2
La velocidad de la partícula para θ/2
1
2
25·
(
1.7·
ω
2
)
2
=
1
2
25·
v
3
2
+25·9.8·(
1.7−1.7·cos
θ
2
)
v
3
=2.32 m/s
Las fuerzas sobre la partícula son:
- La tensión, T
- El peso, mg
Dinámica del movimiento circular uniforme
T−25·9.8cos
θ
2
=25
v
3
2
1.7
T=310.6 N
Problema 4
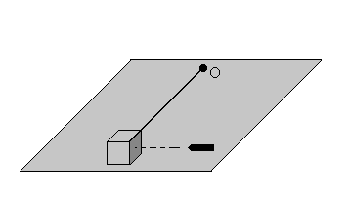 Un cubo de madera de 2 kg y 20 cm de arista, que descansa sobre una
superficie horizontal sin fricción, está sujeto a una barra rígida de longitud
2 m y masa 300 g fijada a la superficie por un extremo en el punto O y por el
otro al centro del cubo. Una bala de masa 50 g y velocidad 200m/s se incrusta
en el cubo a la altura de su centro de masa (en la dirección perpendicular al
cubo, tal como se muestra en la figura)
Un cubo de madera de 2 kg y 20 cm de arista, que descansa sobre una
superficie horizontal sin fricción, está sujeto a una barra rígida de longitud
2 m y masa 300 g fijada a la superficie por un extremo en el punto O y por el
otro al centro del cubo. Una bala de masa 50 g y velocidad 200m/s se incrusta
en el cubo a la altura de su centro de masa (en la dirección perpendicular al
cubo, tal como se muestra en la figura)
- ¿Cuál es la velocidad angular del sistema después del choque?.
- ¿Se conserva
la energía en esta colisión?.
Momentos de inercia respecto de un eje que pasa por el cm del cubo:
I=
1
6
m
a
2
y de la
varilla
I=
1
12
m
L
2
 Solución
Solución
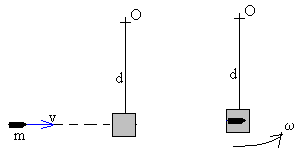
Conservación del momento angular
Momento angular de la partícula respecto de un eje que pasa
por O.
L=mvd
Momento angular del sólido en rotación alrededor de un eje
que pasa por O
L=Iω
Igualamos el momento angular inicial al final
0.05·200·2=(
I
cubo
+
I
varilla
+
I
bala
)ω
0.05·200·2=(
(
1
6
2·
0.2
2
+2·
2
2
)+(
1
12
0.3·
2
2
+0.3·
1
2
)+0.05·
2
2
)ω ω=2.32 rad/s
Energía inicial y final
E
ki
=
1
2
0.05·
200
2
=1000 J
E
kf
=
1
2
I
O
·
ω
2
=23.22 J
Problema 5
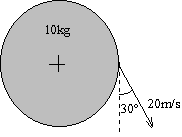 Un disco de masa 10 kg y radio 0.5 m está en reposo y
puede girar en torno a un eje perpendicular al disco y que pasa por su centro.
En la periferia del disco hay un dispositivo de masa despreciable, que permite
lanzar un objeto de 200 g a una velocidad de 20 m/s, en la dirección y sentido
indicado en la figura. Calcular:
Un disco de masa 10 kg y radio 0.5 m está en reposo y
puede girar en torno a un eje perpendicular al disco y que pasa por su centro.
En la periferia del disco hay un dispositivo de masa despreciable, que permite
lanzar un objeto de 200 g a una velocidad de 20 m/s, en la dirección y sentido
indicado en la figura. Calcular:
- La velocidad angular del disco después del disparo
- El sentido en que gira.
- La variación de energía
 Solución
Solución
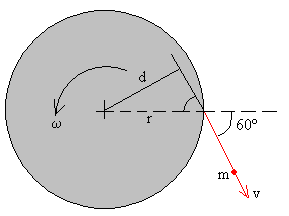
El momento angular de la partícula es
L=r×mv
Su módulo es L=rmvsin60=mvd=0.2·20·0.5·sin60
d es el brazo del momento lineal
La dirección es perpendicular al plano de la pantalla y sentido
hacia dentro
L
1
=−
3
Momento angular del disco
L
2
=Iω=(
1
2
10·
0.5
2
)ω=
5
4
ω
Aplicamos el principio de conservación del momento angular.
- El momento angular inicial es cero
- El momento angular final es la suma del momento angular del
disco y de la partícula que se lanza.
−
3
+
5
4
ω=0 ω=
4
3
5
rad/s
Variación de energía
ΔE=
E
k2
−
E
k1
=
1
2
I
ω
2
+
1
2
m
v
2
=41.2 J
Problema 6
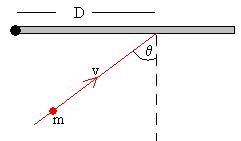 Obtener la fórmula del momento de inercia de una puerta
de masa M, altura b y anchura a, respecto a un eje que
pase a lo largo de su lado b.
Obtener la fórmula del momento de inercia de una puerta
de masa M, altura b y anchura a, respecto a un eje que
pase a lo largo de su lado b.
Una puerta de masa M, se encuentra en reposo y es golpeada por una
bola de masilla de masa m, tal como se muestra en la figura. La velocidad de la
bola de masilla es v, y su dirección inicial es horizontal, formando un ángulo θ con la normal a la cara de la puerta,
impactando a una distancia D del eje de la misma. Después de la colisión
la bola se queda pegada a la puerta. Obtener:
- La expresión de la velocidad de la puerta después de la
colisión.
- La variación de energía cinética del sistema (puerta más
bola de masilla).
Datos m = 1.1 kg, M = 35 kg, a = 73
cm, b = 190 cm, D = 62 cm, θ = 22º, v = 27 m/s.
 Solución
Solución
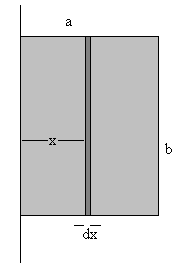 |
Área del elemento diferencial b·dx. Masa dm contenida en dicho elemento
dm=
M
a·b
b·dx=
M
a
dx
I=
∫
x
2
dm
=
∫
0
a
x
2
M
a
dx=
1
3
M
a
2
|
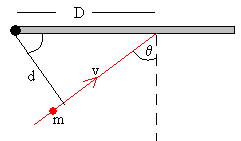
Momento angular inicial de la bola
Li=mv·D·cosθ
Momento angular final de la puerta y la bola pegada
L
f
=(
1
3
M
a
2
+m
D
2
)ω
Aplicamos el principio de conservación del momento angular
L
i
=
L
f
ω=
mvDcosθ
1
3
M
a
2
+m
D
2
ω=2.57 rad/s
Variación de energía
ΔE=
E
kf
−
E
ki
=
1
2
(
1
3
M
a
2
+m
D
2
)
ω
2
−
1
2
m
v
2
=379 J
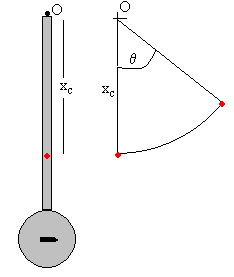
Problema 7
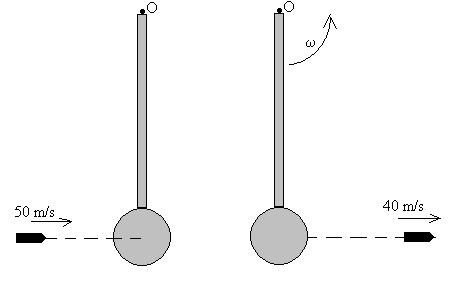
Una bala de 100 g que lleva una velocidad horizontal de 50 m/s choca con
el centro del cilindro de un péndulo. Después del choque la bala se mueve con
una velocidad de 40 m/s. El péndulo gira alrededor de O y está formado por una
varilla delgada de 200 g de masa y 20 cm de longitud, y un cilindro de 500 g de
masa y 5 cm de radio.
- Calcular el ángulo máximo que gira el péndulo como
consecuencia del choque y la energía perdida en el mismo.
 Solución
Solución
Momento de inercia del péndulo respecto de un eje que pasa por el extremo de
la varilla.
I
O
=(
1
12
0.2·
0.2
2
+0.2·
0.1
2
)+(
1
2
0.5·
0.05
2
+0.5·
0.25
2
)=0.034
kgm
2
 Principio de conservación del momento angular
Principio de conservación del momento angular
0.1·50·0.25=IOω+0.1·40·0.25, ω=7.24 rad/s
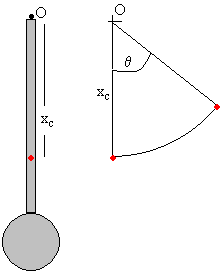
Posición del centro de masa respecto del extremo O de la varilla
x
c
=
0.2·0.1+0.5·0.25
0.2+0.5
=0.21 m
Principio de conservación de la energía. La energía cinética de rotación del
péndulo se transforma en energía potencial de su c.m.
0.7·9.8·(
x
c
−
x
c
cosθ)=
1
2
I
O
ω
2
θ=68.7º
Energía perdida en el choque
ΔE=
1
2
I
O
ω
2
+
1
2
0.1·
40
2
−
1
2
0.1·
50
2
=−44.09 J
Problema 8
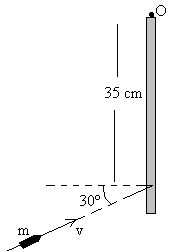 |
Una bala de 100 g de masa y 25
m/s de velocidad choca con una varilla delgada de masa M = 0.9 kg y
longitud L = 45 cm, empotrándose en la misma 35 cm por debajo de su
extremo superior. La varilla puede girar libremente alrededor de un eje
perpendicular al plano del papel, que pasa por O.
- Determinar la
velocidad angular del sistema varilla-bala inmediatamente después del choque.
- Calcular el
máximo desplazamiento angular del sistema varilla-bala.
|
 Solución
Solución
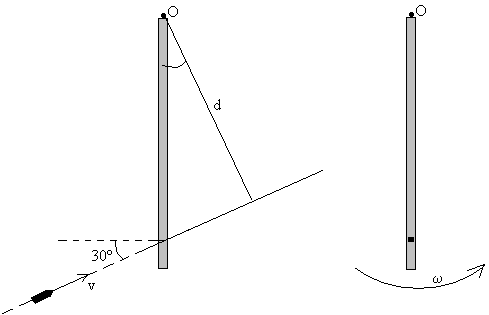
El momento angular de la partícula es
L=r×mv
Su módulo es L =mvd=0.1·25·0.35·cos30
d es el brazo del momento lineal
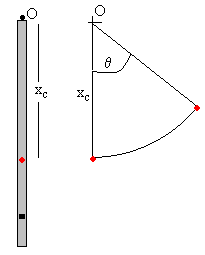 Momento de inercia del péndulo y de la bala incrustada
respecto de un eje que pasa por el extremo O de la varilla
Momento de inercia del péndulo y de la bala incrustada
respecto de un eje que pasa por el extremo O de la varilla
I
o
=(
1
12
0.9·
0.45
2
+0.9·
0.225
2
)+0.1·
0.35
2
=0.073
kgm
2
Principio de conservación del momento angular
mvd=Ioω, ω=10.38 rad/s
Posición del centro de masa respecto del extremo O de la varilla
x
c
=
0.9·0.225+0.1·0.35
0.9+0.1
=0.2375 m
Principio de conservación de la energía. La energía cinética
de rotación del sistema formado por el péndulo y la bala se transforma en
energía potencial de c.m. del sistema.
1.0·9.8·(
x
c
−
x
c
cosθ)=
1
2
I
O
ω
2
θ=133.6º
Problema 9
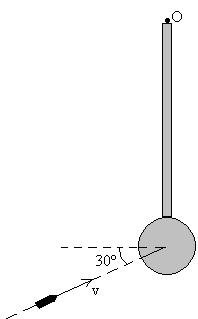 |
Una bala de 100 g que lleva una velocidad de 12.5 m/s
choca con el centro del disco de un péndulo, tal como se muestra en la figura.
Después del choque, la bala queda empotrada en el centro del disco. El péndulo
que gira en torno a un eje perpendicular que pasa por O, está formado por una
varilla delgada de 200 g de masa y 20 cm de longitud y una lenteja de 500 g de
masa y 5 cm de radio.
- Calcular la velocidad angular del sistema inmediatamente
después del choque.
- Calcular el ángulo máximo que gira el péndulo como consecuencia
del choque, y la energía perdida en el mismo.
|
 Solución
Solución
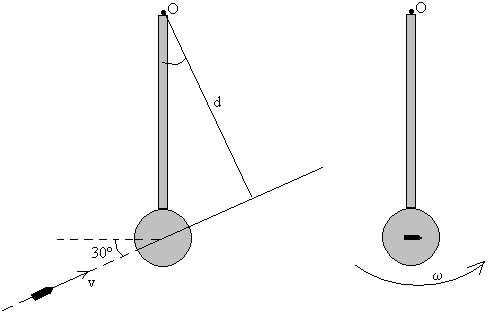
El momento angular de la partícula es
L=r×mv
Su módulo es L =mvd=0.1·12.5·0.25·cos30
d es el brazo del momento lineal
Momento de inercia del péndulo y de la bala incrustada
respecto de un eje que pasa por el extremo O de la varilla
I
o
=(
1
12
0.2·
0.2
2
+0.2·
0.1
2
)+(
1
2
0.5·
0.05
2
+0.5·
0.25
2
)+0.1·
0.25
2
 Principio de conservación del momento angular
Principio de conservación del momento angular
mvd=Ioω, ω=6.634 rad/s
Energía perdida en el choque
ΔE=
1
2
I
O
ω
2
−
1
2
0.1·
12.5
2
=−6.91 J
Posición del centro de masa respecto del extremo O de la varilla
x
c
=
0.5·0.25+0.1·0.25+0.2·0.1
0.5+0.1+0.2
Principio de conservación de la energía. La energía cinética
de rotación del sistema formado por el péndulo y la bala se transforma en
energía potencial de c.m. del sistema.
0.8·9.8·(
x
c
−
x
c
cosθ)=
1
2
I
O
ω
2
θ=62.5º
Problema 10
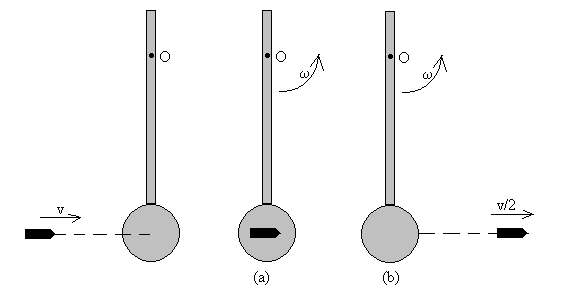
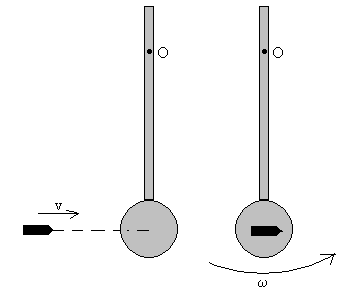
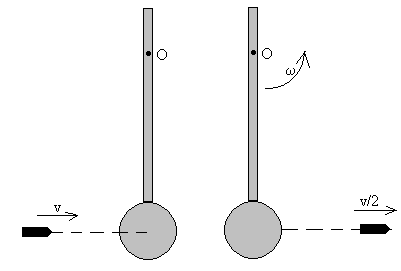
Disparamos una bala de 50 g con velocidad v contra un péndulo compuesto por una esfera y una barra, como indica la figura.
Características de la barra: 40 cm de longitud, 200 g de masa; características
de la esfera: 5 cm de radio y 500 g de masa. La barra está fijada por un punto
O situado a 8 cm de su extremo.
- Si la bala se incrusta en el péndulo, calcular el valor mínimo de v para que el péndulo dé una vuelta completa.
- Si la bala atraviesa el péndulo y sale con velocidad v/2, calcular el
ángulo de desviación máxima al que llegará el péndulo.
 Solución
Solución
Principio de conservación del momento angular
Momento angular de la bala
L=0.05·v·0.37
Momento de inercia del sistema formado por la varilla, la
esfera y la bala incrustada en su centro.
I
o
=(
1
12
0.2·
0.4
2
+0.2·
0.12
2
)+(
2
5
0.5·
0.05
2
+0.5·
0.37
2
)+0.05·
0.37
2
=0.0745
kgm
2
0.05·v·0.37=Io·ω
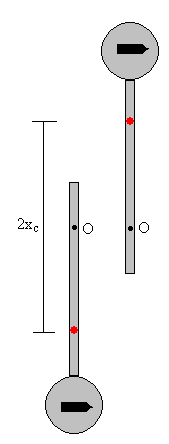 |
Posición del centro de masa respecto de O
x
c
=
0.2
·
0.12
+
0.5
·
0.37
+
0.0.5
·
0.37
0.2
+
0.5
+
0.05
=
0.303
m
Principio de conservación de la energía. La energía cinética
de rotación del sistema formado por el péndulo y la bala se transforma en
energía potencial de c.m. del sistema.
0.75
·
9.8
·
2
x
c
=
1
2
I
O
ω
2
ω
=
10.47
rad/s
De la conservación del momento angular, v=46.04 m/s |
Principio de conservación del momento angular
Momento angular de la bala
L=0.05·v·0.37
Momento angular de la bala y del sistema formado por la
varilla y la esfera
I
o
=(
1
12
0.2·
0.4
2
+0.2·
0.12
2
)+(
2
5
0.5·
0.05
2
+0.5·
0.37
2
)=0.0745
kgm
2
0.05·v·0.37=Io·ω+0.05(v/2)·0.37
como v=46.04
m/s, ω=5.72 rad/s
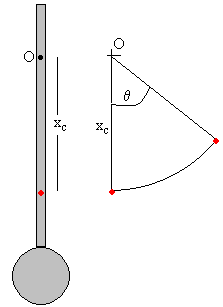 |
Posición del c.m. del sistema formado por la varilla y la
esfera
x
c
=
0.2
·
0.12
+
0.5
·
0.37
0.2
+
0.5
=
0.3
m
Principio de conservación de la energía. La energía cinética
de rotación del sistema formado por la varilla y la esfera se transforma en
energía potencial de c.m. del sistema.
0.7
·
9.8
·
(
x
c
−
x
c
cos
θ
)
=
1
2
I
O
ω
2
θ
=
66.1
º
|
Problema 11
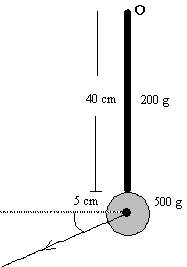 |
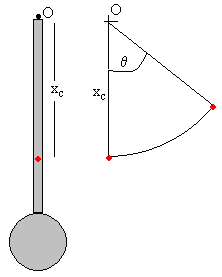
Un péndulo está formado por una varilla delgada de 200 g de masa y 20 cm
de longitud y una lenteja de forma cilíndrica 500 g de masa y 5 cm de radio. En
el centro de la lenteja hay un dispositivo que lanza una partícula de 100 g con
una velocidad de 12.5 m/s haciendo un ángulo de 30º con la horizontal tal como
se muestra en la figura.
- Calcular la velocidad angular del péndulo inmediatamente después del
disparo de la partícula.
- Calcular el máximo desplazamiento angular del péndulo
|
 Solución
Solución
El momento angular inicial es cero
El momento angular de la partícula es L=r×mv
Su módulo es L =mvd=0.1·12.5·0.45·cos30
d es el brazo del momento lineal
Su sentido es el de las agujas del reloj (-)
Momento de inercia del péndulo respecto de un eje que pasa
por el extremo O de la varilla
I
o
=(
1
12
0.2·
0.4
2
+0.2·
0.2
2
)+(
1
2
0.5·
0.05
2
+0.5·
0.45
2
)
Principio de conservación del momento angular
-mvd+Ioω=0, ω=4.33 rad/s
 |
Posición del centro de masa respecto del extremo O de la varilla del péndulo
x
c
=
0.2
·
0.2
+
0.5
·
0.45
0.2
+
0.5
=
0.38
m
Principio de conservación de la energía. La energía cinética
de rotación del péndulo se transforma en energía potencial de su c.m..
0.7
·
9.8
·
(
x
c
−
x
c
cos
θ
)
=
1
2
I
O
ω
2
θ
=
53.5
º
|
Problema 12
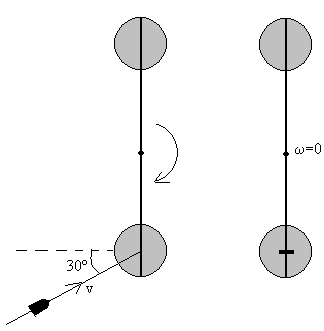
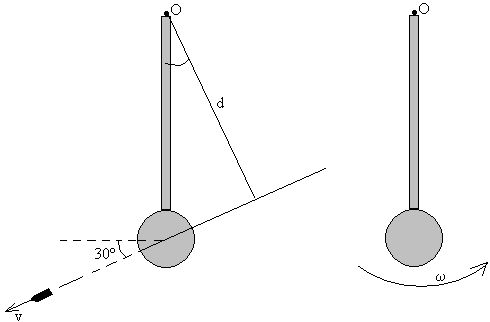
Un sólido rígido en rotación en el plano horizontal con
velocidad angular constante de 120 rpm, está formado por una varilla delgada de
2 kg de masa y 80 cm de longitud y dos esferas iguales de 6 kg y 10 cm de
radio, tal como se muestra en la figura. Se dispara una bala de 300 g con
velocidad v haciendo 30º con la horizontal. La bala se incrusta en el
centro de la esfera.
- Cuál debe ser la velocidad v para que el sistema se
pare después del choque.
 Solución
Solución
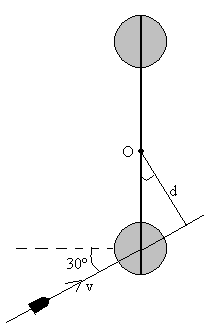
El momento angular de la bala es L=r×mv
Su módulo es L =mvd=0.3·v·0.3·cos30
d es el brazo del momento lineal
Su sentido es contrario al de las agujas del reloj (+)
Momento de inercia del sólido de un eje que pasa por O
I
o
=(
1
12
2·
0.8
2
)+2(
2
5
6·
0.1
2
+6·
0.3
2
)=1.23
kgm
2
Momento angular del sólido en rotación Ioω, con ω=4π rad/s
Su sentido es el de las agujas del reloj (-)
El momento angular final es cero
Principio de conservación del momento angular
mvd-Ioω=0, v=199 m/s
Problema 13
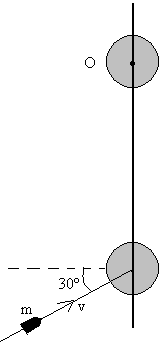 |
Un péndulo está formado por una varilla de 200 g de masa
y 40 cm de longitud y dos esferas macizas: la superior de 500 g y 5cm de radio
y la inferior de 400 g y 4 cm de radio, equidistantes 8 cm de los extremos de
la barra. El péndulo se encuentra suspendido de un eje perpendicular a la varilla
que pasa por el centro de la esfera superior. Sobre el centro de la esfera
inferior incide una bala de 50 g y 10 m/s de velocidad que queda alojada en el
centro de la esfera. Calcular
- Desplazamiento angular máximo del péndulo
|
 Solución
Solución
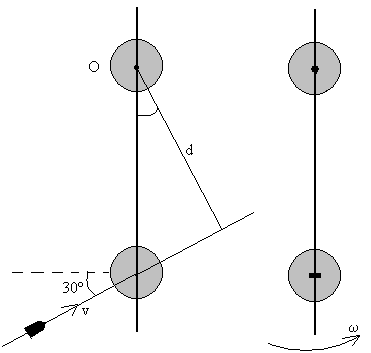
El momento angular de la partícula es L=r×mv
Su módulo es L =mvd=0.05·10·0.24·cos30
d es el brazo del momento lineal
Momento de inercia del sistema formado por el péndulo y la
bala incrustada respecto de un eje que pasa por O
I
o
=(
1
12
0.2·
0.4
2
+0.2·
0.12
2
)+
2
5
0.5·
0.05
2
+(
2
5
0.4·
0.04
2
+0.4·
0.24
2
)+0.05·
0.24
2
=0.0322
kgm
2
Principio de conservación del momento angular
mvd=Ioω=0, ω=3.225 rad/s
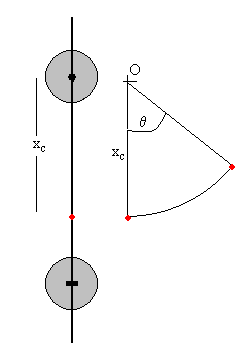 |
Posición del centro de masa respecto de O
x
c
=
0.2
·
0.12
+
0.4
·
0.24
+
0.05
·
0.24
0.5
+
0.2
+
0.4
+
0.05
=
0.115
m
Principio de conservación de la energía. La energía cinética
de rotación del sistema formado por el péndulo y la bala se transforma en
energía potencial de su c.m..
1.15
·
9.8
·
(
x
c
−
x
c
cos
θ
)
=
1
2
I
O
ω
2
θ
=
29.5
º
|


 Dos esferas iguales de masas 6 kg y 20 cm de radio están montadas como se
indica en la figura, y pueden deslizar a lo largo de una varilla delgada de 3 kg
de masa y 2 m de longitud. El conjunto gira libremente con una velocidad
angular de 120 rpm respecto a un eje vertical que pasa por el centro del
sistema.
Dos esferas iguales de masas 6 kg y 20 cm de radio están montadas como se
indica en la figura, y pueden deslizar a lo largo de una varilla delgada de 3 kg
de masa y 2 m de longitud. El conjunto gira libremente con una velocidad
angular de 120 rpm respecto a un eje vertical que pasa por el centro del
sistema.  Solución
Solución
 Solución
Solución
 Solución
Solución Un cubo de madera de 2 kg y 20 cm de arista, que descansa sobre una
superficie horizontal sin fricción, está sujeto a una barra rígida de longitud
2 m y masa 300 g fijada a la superficie por un extremo en el punto O y por el
otro al centro del cubo. Una bala de masa 50 g y velocidad 200m/s se incrusta
en el cubo a la altura de su centro de masa (en la dirección perpendicular al
cubo, tal como se muestra en la figura)
Un cubo de madera de 2 kg y 20 cm de arista, que descansa sobre una
superficie horizontal sin fricción, está sujeto a una barra rígida de longitud
2 m y masa 300 g fijada a la superficie por un extremo en el punto O y por el
otro al centro del cubo. Una bala de masa 50 g y velocidad 200m/s se incrusta
en el cubo a la altura de su centro de masa (en la dirección perpendicular al
cubo, tal como se muestra en la figura) Solución
Solución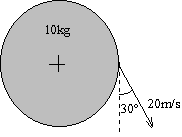 Un disco de masa 10 kg y radio 0.5 m está en reposo y
puede girar en torno a un eje perpendicular al disco y que pasa por su centro.
En la periferia del disco hay un dispositivo de masa despreciable, que permite
lanzar un objeto de 200 g a una velocidad de 20 m/s, en la dirección y sentido
indicado en la figura. Calcular:
Un disco de masa 10 kg y radio 0.5 m está en reposo y
puede girar en torno a un eje perpendicular al disco y que pasa por su centro.
En la periferia del disco hay un dispositivo de masa despreciable, que permite
lanzar un objeto de 200 g a una velocidad de 20 m/s, en la dirección y sentido
indicado en la figura. Calcular:  Solución
Solución Obtener la fórmula del momento de inercia de una puerta
de masa M, altura b y anchura a, respecto a un eje que
pase a lo largo de su lado b.
Obtener la fórmula del momento de inercia de una puerta
de masa M, altura b y anchura a, respecto a un eje que
pase a lo largo de su lado b. Solución
Solución
 Solución
Solución
 Solución
Solución
 Solución
Solución
 Solución
Solución
 Solución
Solución
 Solución
Solución
 Solución
Solución






 Tensión de la cuerda para θ/2
Tensión de la cuerda para θ/2



 Principio de conservación del momento angular
Principio de conservación del momento angular
 Momento de inercia del péndulo y de la bala incrustada
respecto de un eje que pasa por el extremo O de la varilla
Momento de inercia del péndulo y de la bala incrustada
respecto de un eje que pasa por el extremo O de la varilla
 Principio de conservación del momento angular
Principio de conservación del momento angular







