Los anillos de un planeta

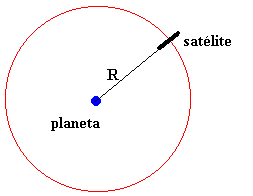satelite.gif (1238 bytes) En esta página, vamos a comprobar la formación de un anillo alrededor de un planeta. Supondremos que el planeta tiene un satélite en forma de disco con su diámetro dirigido hacia el centro del planeta y que el centro del disco describe una órbita circular.

En un momento dado, el satélite se rompe en múltiples fragmentos. Estudiaremos el movimiento de cada uno de ellos, y veremos como al cabo de un cierto tiempo se disponen formando un anillo alrededor del planeta.

Para simplificar el problema, supondremos que los fragmentos son masas puntuales, y su atracción mutua es despreciable frente a la atracción dominante del planeta.

Descripción

Aplicaremos la dinámica del movimiento circular uniforme para describir el movimiento del centro de masas de un satélite de masa m en órbita circular de radio R alrededor del planeta de masa M.

La segunda ley de Newton expresa que la fuerza de atracción es igual al producto de la masa por la aceleración normal.

$\frac{G M m}{R^{2}} = m \frac{v_{c}^{2}}{R}$

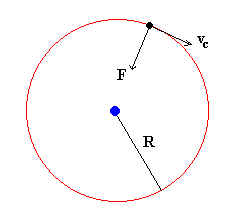circunferencia.gif (1172 bytes) De esta ecuación se despeja la velocidad lineal v_c del centro del satélite y la velocidad angular ω de rotación, que son respectivamente.

$v_{c} = \sqrt{\frac{G M}{R}} ω = \frac{v_{c}}{R} = \sqrt{\frac{G M}{R^{3}}}$

La velocidad v₀ de un fragmento el planeta en forma de disco a una distancia r₀ del centro del planeta vale v₀=ωr₀.

En el momento en el que se rompe el satélite la energía y el momento angular de cada fragmento valen respectivamente

$\begin{array}{l} E = \frac{1}{2} m v_{0}^{2} - \frac{G M m}{r_{0}} = \frac{1}{2} m \frac{G M}{R^{3}} r_{0}^{2} - \frac{G M m}{r_{0}} \\ L = m v_{0} r_{0} = m \sqrt{\frac{G M}{R^{3}}} r_{0}^{2} \end{array}$

Para que los fragmentos se mantengan describiendo órbitas alrededor del planeta, es necesario que sus energías totales sean negativas (E<0). Esto impone un tamaño máximo al satélite. La distancia del fragmento del satélite más alejado del centro del planeta ha de ser inferior a $r_{0} < \sqrt[3]{2} R$ . Por lo que el diámetro del satélite deberá ser inferior a $2 (\sqrt[3]{2} R - R) \approx 0.5 R$

Como la fuerza que actúa sobre cada fragmento es central y conservativa, las magnitudes energía total E y momento angular L, se mantienen constantes a lo largo de su trayectoria, una elipse que en coordenadas polares

$r = \frac{d}{1 + ε \cos θ} d = \frac{L^{2}}{G M m^{2}} ε = \sqrt{1 + \frac{2 L^{2} E}{G^{2} M^{2} m^{3}}}$

El periodo de la órbita de un fragmento vale

$P = \frac{2 m π a b}{L}$

siendo a el semieje mayor y b el semieje menor de órbita elíptica.

Introduciendo en los parámetros d y excentricidad ε los valores de la energía y del momento angular de cada uno de los fragmentos, se obtiene

$d = \frac{r_{0}^{4}}{R^{3}} ε = | \frac{r_{0}^{3}}{R^{3}} - 1 |$

Para obtener el valor del periodo, hemos de calcular el semieje mayor a y el semieje menor b de la elipse. Ya hemos visto que la relación entre los semiejes de la elipse y la semidistancia focal c es

$a^{2} = b^{2} + c^{2} ε = \frac{c}{a}$

y la relación entre el semieje mayor a de la elipse y las distancias más alejada r₁ y más cercana al foco r₂.

$r_{1} = \frac{d}{1 - ε} r_{2} = \frac{d}{1 + ε} 2 a = r_{1} + r_{2}$

Efectuando algunas operaciones, obtenemos el periodo P de un fragmento situado a una distancia inicial r₀ del centro del planeta.

$P = P_{0} {(\frac{r_{0}}{2 R^{3} - r_{0}^{3}})}^{3 / 2} P_{0} = \frac{2 π R}{v_{c}}$

donde P₀ es el periodo del centro del satélite en su órbita circular.

Vemos, por tanto, que distintos fragmentos tienen periodos distintos, lo que da lugar a que se retrasen o se adelanten respecto del centro del satélite original. En la siguiente tabla se proporcionan algunos valores

r₀/R	P/P₀
1	1
1.01	1.06
0.99	0.94
1.10	2.11
0.90	0.59

Actividades

En el programa, el radio de la órbita circular del satélite alrededor del planeta se toma como unidad, se introduce el diámetro del satélite menor que 0.5 en el control de edición titulado Diámetro del satélite.

Se introduce el número de fragmentos en el que se rompe el satélite en el control de edición titulado Número de fragmentos.

Se observa el movimiento del satélite pulsando en el botón titulado Nuevo.

Se observa el movimiento de los fragmentos del satélite pulsando en el botón titulado Rompe.

Para observar un anillo formado por los fragmentos del satélite girando alrededor del planeta, introducir valores tal como

Diámetro del satélite, 0.01
Número de fragmentos, 100.