• Inicio
• Dinámica celeste
• Fuerza central y conservativa

Fuerza central y conservativa

Fuerza de atracción entre los cuerpos

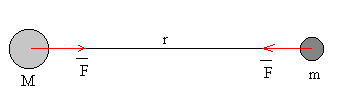La interacción entre dos cuerpos de masa M y m se describe en término de una fuerza atractiva, cuya dirección es la recta que pasa por el centro de los dos cuerpos y cuyo módulo viene dado por la expresión

${\displaystyle F=G\frac{Mm}{r^2}}$

G es la constante de la gravitación universal G=6.67·10^-11 Nm²/kg², y r es la distancia entre los centros de los cuerpos

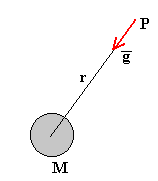
Aceleración de la gravedad Se denomina intensidad del campo gravitatorio, o aceleración de la gravedad g en un punto P distante r del centro del planeta de masa M, a la fuerza sobre la unidad de masa situada en el punto P. ${\displaystyle g=\frac{F}{m}=G\frac{M}{r^2}}$

Fuerza central

La fuerza de atracción entre un planeta y el Sol es central y conservativa. La fuerza de repulsión entre una partícula alfa y un núcleo es también central y conservativa. En este apartado estudiaremos la primera, dejando para más adelante la segunda, en el estudio del fenómeno de la dispersión, que tanta importancia tuvo en el descubrimiento de la estructura atómica.

Una fuerza es central, cuando el vector posición r es paralelo al vector fuerza F. El momento de la fuerza M=r×F=0. De la relación entre le momento de las fuerzas que actúa sobre la partícula y el momento angular, (Teorema del momento angular) se concluye que

${\displaystyle M=\frac{dL}{dt}M=0L=\text{cte}}$

El momento angular permanece constante en módulo, dirección y sentido.El momento angular L de una partícula es el vector resultado del producto vectorial L=r×mv, cuya dirección es perpendicular al plano determinado por el vector posición r y el vector velocidad v. Como el vector L permanece constante en dirección, r y v estarán en un plano perpendicular a la dirección fija de L.

De aquí, se concluye que la trayectoria del móvil estará contenida en un plano perpendicular al vector momento angular L. Cuando los vectores r y v son paralelos, es decir, la dirección del movimiento pasa por el origen, el momento angular L=0. La partícula describe un movimiento rectilíneo, cuya aceleración no es constante.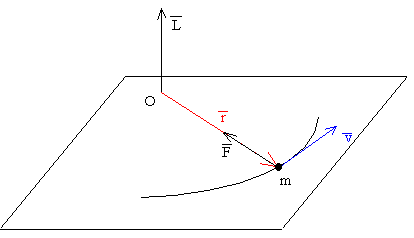 

Fuerza conservativa

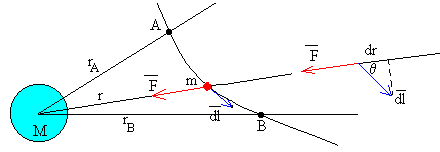
Supongamos que una partícula de masa m se mueve desde la posición A hasta la posición B en las proximidades de un cuerpo fijo de masa M.Vamos a calcular el trabajo realizado por la fuerza de atracción F. 

${\displaystyle F=-\frac{GMm}{r^2}\widehat{r}}$

El trabajo infinitesimal es el producto escalar del vector fuerza F por el vector desplazamiento dl, tangente a la trayectoria.

 dW=F·dl=F·dl·cos(180-θ)=-F·dl·cosθ=-F·dr. 

donde dr es el desplazamiento infinitesimal de la partícula en la dirección radial.Para calcular el trabajo total, integramos entre la posición inicial A, distante r_A del centro de fuerzas y la posición final B, distante r_B del centro fijo de fuerzas.

${\displaystyle W={\displaystyle \underset{A}{\overset{B}{\int }}-G\frac{Mm}{r^2}dr=G\frac{Mm}{r_B}}-G\frac{Mm}{r_A}=\left(-G\frac{Mm}{r_A}\right)-\left(-G\frac{Mm}{r_A}\right)}$

El trabajo W no depende del camino seguido por la partícula para ir desde la posición A a la posición B.

La fuerza de atracción F, que ejerce el cuerpo fijo de masa M sobre la partícula de masa m es conservativa.  La fórmula de la energía potencial es 

${\displaystyle E_p=\frac{-GMm}{r}}$

El nivel cero de energía potencial se ha establecido en el infinito, para r=∞, E_p=0

El hecho de que la fuerza de atracción sea conservativa, implica que la energía total (cinética más potencial) de la partícula es constante, en cualquier punto de la trayectoria.

${\displaystyle E=\frac{1}{2}m{v}^2+E_p=\text{cte}}$

Movimiento de los cuerpos celestes

Cuando el momento angular L no es nulo, la trayectoria es una cónica, tal como demostraremos en la siguiente página.

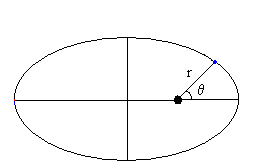Para obtener ecuación de la trayectoria r=r(θ) se expresa el momento angular y la energía en coordenadas polares y se integra la ecuación diferencial resultante. El parámetro ε, denominado excentricidad, define el tipo de trayectoria

${\displaystyle r=\frac{d}{1+\epsilon \cos (\theta )}\epsilon =\sqrt{1+\frac{2L^{2}E}{m^3{G}^2{M}^2}}d=\frac{L^2}{GM{m}^2}}$

Clase de cónica	Descripción geométrica	Descripción física
Elipse	ε<1	E<0
Parábola	ε=1	E=0
Hipérbola	ε>1	E>0

Así, una elipse se define en geometría como el tipo de cónica cuya excentricidad es menor que la unidad. Para que una partícula sometida a una fuerza central, atractiva, inversamente proporcional al cuadrado de las distancias al centro de fuerzas, describa dicha trayectoria tiene que tener una energía total negativa (E<0).

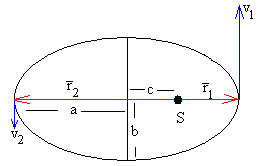
Volviendo a la geometría de la elipse en la primera ley de Kepler, la posición más cercana al foco r₁ se obtiene cuando θ=0 y la posición más alejada r₂ se obtiene cuando θ=π. Es decir,

${\displaystyle r_1=\frac{d}{1+\epsilon }{r}_2=\frac{d}{1-\epsilon }}$

Los semiejes a y b de la elipse valen

${\displaystyle \begin{array}{l}2a=r_2+r_{1}a=\frac{d}{1-{\epsilon }^2}\\ a^2=b^2+c^{2}b=a\sqrt{1-{\epsilon }^2}\end{array}}$

El semieje mayor de la elipse a es independiente del momento angular L, y solamente depende de la energía total E. El semieje menor b depende del momento angular L y de la energía E

${\displaystyle a=-\frac{mGM}{2E}b=\frac{L\sqrt{a}}{m\sqrt{GM}}}$

Periodo

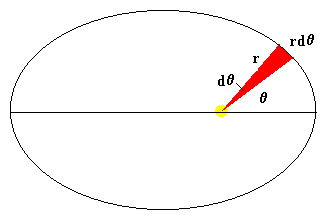Se denomina periodo, al tiempo que tarda el móvil en dar una vuelta completa. En el applet que estudia la segunda ley de Kepler y en la figura vemos que el radio vector que une el Sol con el planeta barre en el intervalo de tiempo comprendido entre t y t+dt el área de color rojo de forma triangular.

El ángulo del vértice de dicho triángulo es dθ y la base del triángulo es un arco de longitud rdθ. El área del triángulo  es (base por altura dividido por dos)

${\displaystyle \frac{r(r·d\theta )}{2}=\frac{r^{2}d\theta }{2}}$

Integrando la ecuación del momento angular expresado en coordenadas polares

${\displaystyle {\displaystyle \underset{0}{\overset{2\pi }{\int }}{r}^{2}d\theta }={\displaystyle \underset{0}{\overset{P}{\int }}\frac{L}{m}}dt{\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{r^{2}d\theta }{2}}=\frac{L}{2m}{\displaystyle \underset{0}{\overset{P}{\int }}dt}}$

La primera integral es el área total de la elipse πab, que es igual a la suma de las áreas de todos triángulos infinitesimales. La integral del segundo miembro es el periodo P del planeta, por tanto

${\displaystyle P=\frac{2m\pi ab}{L}}$

Poniendo el semieje b en función del semieje a, (final del apartado anterior) llegamos a la fórmula que relaciona el periodo de la órbita de un planeta P y el semieje mayor de la elipse a, denominada tercera ley de Kepler.

${\displaystyle P^2=\frac{4{\pi }^2{a}^3}{\left(GM\right)}}$

Curso Interactivo de Física en Internet © Ángel Franco García