• Inicio
• Dinámica celeste
• Fuerza central y conservativa

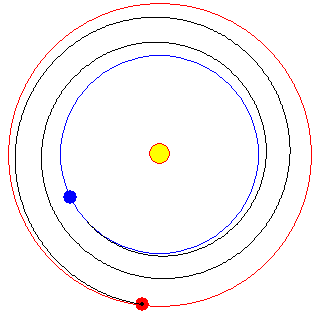
Viaje de la Tierra a Marte siguiendo una trayectoria en forma de espiral logarítmica.

En las páginas anteriores, hemos visto que una nave espacial puede pasar de una órbita circular de baja altura a una órbita circular de mayor altura a través de una órbita semielíptica de transferencia. El motor proporciona a la nave dos impulsos de pequeña duración. El primero, para colocarla en la órbita de transferencia y el segundo, para situarla en la órbita circular de destino.

En esta página, se va a describir, una órbita de transferencia en forma de espiral logarítmica que une dos órbitas circulares de distinto radio. Para que la nave siga esta trayectoria solamente es necesario un motor que proporcione una aceleración relativamente pequeña a lo largo del viaje y que va disminuyendo a medida que la nave se aleja del centro de fuerzas.

Como ejemplo significativo, vamos a describir el viaje de una nave espacial desde las proximidades de la Tierra (pero fuera de su esfera de influencia) hasta las proximidades del planeta Marte. En color negro, se muestra la trayectoria espiral de la nave espacial.

Posición, velocidad y aceleración en coordenadas polares

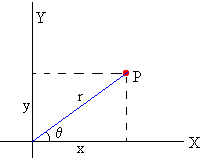La posición del punto P es x=r·cosθ y=r·sinθ

En coordenadas polares, un eje tiene la dirección radial y el otro eje, la dirección perpendicular a la radial, tal como se muestra en la figura.

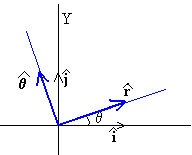Las componentes de los vectores unitarios r y θ son ${\displaystyle \begin{array}{l}\widehat{r}=\widehat{i}\cos \theta +\widehat{j}\text{sin}\theta \\ \widehat{\theta }=-\widehat{i}\text{sin}\theta +\widehat{j}\cos \theta \end{array}}$

Derivando con respecto del tiempo

${\displaystyle \begin{array}{l}\frac{d\widehat{r}}{dt}=(-\widehat{i}\text{sin}\theta +\widehat{j}\cos \theta )\frac{d\theta }{dt}=\widehat{\theta }\frac{d\theta }{dt}\\ \frac{d\widehat{\theta }}{dt}=(-\widehat{i}\text{cos}\theta -\widehat{j}\text{sin}\theta )\frac{d\theta }{dt}=-\widehat{r}\frac{d\theta }{dt}\end{array}}$

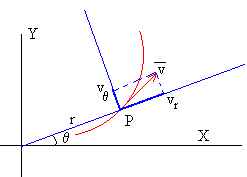La velocidad se expresa en coordenadas polares de la siguiente forma ${\displaystyle v=\frac{dr}{dt}=r\frac{d\widehat{r}}{dt}+\widehat{r}\frac{dr}{dt}=\frac{dr}{dt}\widehat{r}+r\frac{d\theta }{dt}\widehat{\theta }}$

La aceleración se expresa en coordenadas polares

${\displaystyle \begin{array}{l}a=\frac{dv}{dt}=\frac{d^{2}r}{d{t}^2}\widehat{r}+\frac{dr}{dt}\frac{d\widehat{r}}{dt}+r\frac{d^2\theta }{d{t}^2}\widehat{\theta }+\frac{dr}{dt}\frac{d\theta }{dt}\widehat{\theta }+r\frac{d\theta }{dt}\frac{d\widehat{\theta }}{dt}=\\ \frac{d^{2}r}{d{t}^2}\widehat{r}+\frac{dr}{dt}\frac{d\theta }{dt}\widehat{\theta }+r\frac{d^2\theta }{d{t}^2}\widehat{\theta }+\frac{dr}{dt}\frac{d\theta }{dt}\widehat{\theta }-r\frac{d\theta }{dt}\frac{d\theta }{dt}\widehat{r}=\\ \left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)\widehat{r}+\left(r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}\right)\widehat{\theta }\end{array}}$

La espiral logarítmica

La espiral logarítmica es una de las curvas notables o maravillosas junto a la catenaria, la cicloide, etc.

La ecuación de la espiral logarítmica en coordenadas polares es

r=r₀·exp(b·θ)

Donde r₀ es el radio inicial, b es un parámetro, y θ es el ángulo en radianes.

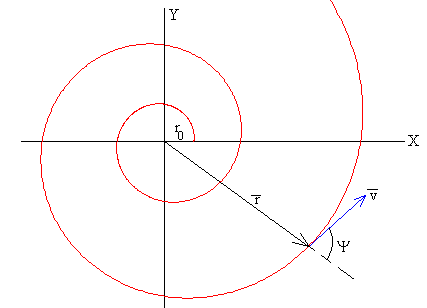
La principal característica de la espiral logarítmica es que el radio vector r, y la tangente a la espiral forman un ángulo Ψ que se mantiene constante.

La velocidad v de la partícula que describe una espiral logarítmica es

${\displaystyle v=\frac{dr}{dt}=\frac{dr}{dt}\widehat{r}+r\frac{d\theta }{dt}\widehat{\theta }=r(b\widehat{r}+\widehat{\theta })}$

Calculamos el ángulo Ψ entre los vectores v y r, empleando la definición de producto escalar de dos vectores.

${\displaystyle \cos \Psi =\frac{v\cdot r}{v·r}=\frac{b}{\sqrt{b^2+1}}b=\frac{1}{\tan \Psi }=\cot \Psi }$

Cuando b→0, Ψ→π/2 y r→r₀, la espiral logarítmica se convierte en una circunferencia de radio r₀.

Longitud de un arco de la espiral logarítmica

La longitud de un arco infinitesimal ds es el módulo del vector desplazamiento dr.

${\displaystyle ds=\sqrt{{(dr)}^2+{(r·d\theta )}^2}}$

La longitud del arco de espiral logarítmica entre θ=0 y θ es

${\displaystyle {\displaystyle \underset{0}{\overset{s}{\int }}ds}={\displaystyle \underset{0}{\overset{\theta }{\int }}\sqrt{{(dr)}^2+{(r·d\theta )}^2}}={\displaystyle \underset{0}{\overset{\theta }{\int }}\sqrt{1+b^2}{r}_0{e}^{b\theta }}d\theta =\frac{\sqrt{1+b^2}}{b}{r}_0\left(e^{b\theta }-1\right)=\frac{\sqrt{1+b^2}}{b}(r-r_0)}$

Ecuaciones del movimiento

Supondremos que el motor de la nave espacial de masa m proporciona una fuerza de empuje F que tiene la misma dirección que la velocidad de la nave, es decir, es tangente a la trayectoria.

Las fuerzas que actúan sobre la nave espacial son:

• La fuerza de empuje F de los motores de la nave

• La fuerza de atracción del Sol, GMm/r² se supone que la nave espacial está fuera de las esferas de influencia de la Tierra (cuando sale) y de Marte (cuando llega).

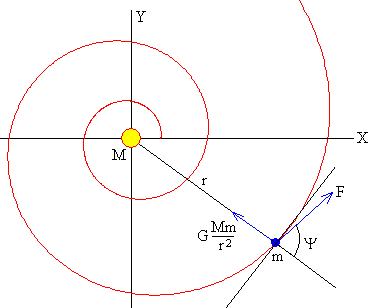
En coordenadas polares, la ecuación del movimiento se escribe

${\displaystyle \begin{array}{l}m\left(\frac{d^{2}r}{d{t}^2}-r{\left(\frac{d\theta }{dt}\right)}^2\right)=F\cos \Psi -G\frac{Mm}{r^2}\\ m\left(r\frac{d^2\theta }{d{t}^2}+2\frac{dr}{dt}\frac{d\theta }{dt}\right)=F\text{sin}\Psi \end{array}}$

Como la ecuación de la trayectoria es r=r₀·exp(θ·cotΨ), calculamos la derivada primera y segunda de r con respecto del tiempo t

${\displaystyle \begin{array}{l}\frac{dr}{dt}=r\frac{d\theta }{dt}\cot \Psi \\ \frac{d^{2}r}{d{t}^2}=r{\left(\frac{d\theta }{dt}\right)}^2{\cot }^2\Psi +r\frac{d^2\theta }{d{t}^2}\cot \Psi \end{array}}$

Introducimos estas expresiones en las ecuaciones del movimiento

${\displaystyle \begin{array}{l}\left(r{\left(\frac{d\theta }{dt}\right)}^2({\cot }^2\Psi -1)+r\frac{d^2\theta }{d{t}^2}\cot \Psi \right)=\frac{F}{m}\cos \Psi -G\frac{M}{r^2}\\ \left(r\frac{d^2\theta }{d{t}^2}+2r{\left(\frac{d\theta }{dt}\right)}^2\cot \Psi \right)=\frac{F}{m}\text{sin}\Psi \end{array}}$

Despejamos rd²θ/dt² en la segunda ecuación y la introducimos en la primera, se obtiene la ecuación

${\displaystyle \begin{array}{l}r{\left(\frac{d\theta }{dt}\right)}^2({\cot }^2\Psi +1)=G\frac{M}{r^2}\\ \frac{d\theta }{dt}=\frac{\sqrt{GM}\text{sin}\Psi }{r^{3/2}}\end{array}}$

Sabiendo que la ecuación de la trayectoria es r=r₀·exp(θ·cotΨ), integramos esta ecuación diferencial para obtener la variación del ángulo θ con el tiempo t.

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\theta }{\int }}\exp \left(\frac{3}{2}\theta ·\cot \Psi \right)}d\theta ={\displaystyle \underset{0}{\overset{t}{\int }}\frac{\sqrt{GM}\text{sin}\Psi }{r_0^{3/2}}dt}\\ \exp \left(\frac{3}{2}\theta ·\cot \Psi \right)=1+\frac{3}{2}\cos \Psi \sqrt{\frac{GM}{r_0^3}}t\end{array}}$

Teniendo en cuenta que la derivada primera de r respecto del tiempo t es

${\displaystyle \frac{dr}{dt}=r\frac{d\theta }{dt}\cot \Psi }$

Transformamos la ecuación diferencial en θ en una ecuación diferencial similar en r.

${\displaystyle \begin{array}{l}\frac{d\theta }{dt}=\frac{\sqrt{GM}\text{sin}\Psi }{r^{3/2}}\\ \frac{dr}{dt}=\frac{\sqrt{GM}\cos \Psi }{r^{1/2}}\end{array}}$

Integramos esta ecuación diferencial para obtener la variación del radio r con el tiempo t.

${\displaystyle \begin{array}{l}{\displaystyle \underset{r_0}{\overset{r}{\int }}\sqrt{r}dr}={\displaystyle \underset{0}{\overset{t}{\int }}\sqrt{GM}\text{cos}\Psi ·dt}\\ r^{3/2}=r_0^{3/2}+\frac{3}{2}\sqrt{GM}\cos \Psi ·t\end{array}}$

Las ecuaciones paramétricas (en función del tiempo t) de la trayectoria son

${\displaystyle \begin{array}{l}r={\left(r_0^{3/2}+\frac{3}{2}\sqrt{GM}\cos \Psi ·t\right)}^{2/3}\\ \theta =\frac{2\tan \Psi }{3}\ln \left(1+\frac{3}{2}\cos \Psi \sqrt{\frac{GM}{r_0^3}}t\right)\end{array}}$

Velocidad de la nave espacial

El módulo de la velocidad de la nave espacial en coordenadas polares es

${\displaystyle v=\sqrt{{\left(\frac{dr}{dt}\right)}^2+{\left(r\frac{d\theta }{dt}\right)}^2}=\sqrt{\frac{GM{\cos }^2\Psi }{r}+r^2\frac{GM{\text{sin}}^2\Psi }{r^3}}=\sqrt{\frac{GM}{r}}}$

es igual a la velocidad de una nave espacial que describa una órbita circular de radio r.

Fuerza de empuje sobre la nave espacial

La segunda ecuación del movimiento, nos permite calcular el módulo de la fuerza F de empuje de los motores de la nave.

${\displaystyle \left(r\frac{d^2\theta }{d{t}^2}+2r{\left(\frac{d\theta }{dt}\right)}^2\cot \Psi \right)=\frac{F}{m}\text{sin}\Psi }$

Conocemos la expresión de la derivada primera dθ/dt y calculamos la derivada segunda  d²θ/dt² del ángulo θ respecto del tiempo t. Para ello, combinamos las ecuaciones

${\displaystyle r^3{\left(\frac{d\theta }{dt}\right)}^2=GM{\text{sin}}^{\text{2}}\Psi }$

 r=r₀·exp(θ·cotΨ),

para obtener la expresión

${\displaystyle \exp (3\theta ·\cot \Psi ){\left(\frac{d\theta }{dt}\right)}^2=\frac{GM{\text{sin}}^{\text{2}}\Psi }{r_0^3}}$

Derivando con respecto del tiempo, y teniendo en cuenta que el segundo miembro es constante.

${\displaystyle \frac{d^2\theta }{d{t}^2}=-\frac{3\cot \Psi }{2}{\left(\frac{d\theta }{dt}\right)}^2=-\frac{3GM\text{sin}\Psi \cos \Psi }{2r^3}}$

Ahora, se despeja de la segunda ecuación del movimiento la fuerza de empuje

${\displaystyle \frac{F}{m}=\frac{1}{2}\frac{GM\cos \Psi }{r^2}}$  

El empuje F necesario para que la nave espacial describa una trayectoria en forma de espiral logarítmica va disminuyendo de forma inversamente proporcional al cuadrado de la distancia r al Sol. Su dirección es la misma que la velocidad (tangente a la trayectoria).

Tiempo de viaje

El tiempo de viaje T a un planeta que dista r del Sol es

${\displaystyle T=\frac{2(r^{3/2}-r_0^{3/2})}{3\sqrt{GM}\cos \Psi }}$

La posición angular θ de la nave espacial en función del tiempo t es

${\displaystyle \theta =\frac{2\tan \Psi }{3}\ln \left(1+\frac{3}{2}\cos \Psi \sqrt{\frac{GM}{r_0^3}}t\right)}$

Introducimos el valor del tiempo de viaje t=T, obtenemos después de simplificar

${\displaystyle {\theta }_f=\ln \left(\frac{r}{r_0}\right)\tan \Psi }$

Ejemplo

• La Tierra describe una órbita aproximadamente circular alrededor del Sol de radio r₀=1.0 UA=1.496·10¹¹ m.

• Marte describe una órbita aproximadamente circular alrededor del Sol de radio r=1.524 UA=2.280·10¹¹ m.

• La masa del Sol es M=1.98·10³⁰ kg

• La constante G=6.67·10^-11 Nm²/kg²

Aplicando la ecuación de la dinámica del movimiento circular uniforme calculamos la velocidad angular de Marte en su órbita circular alrededor del Sol.

${\displaystyle G\frac{Mm}{r_M^2}=m{\omega }_M^2{r}_M}$

ω_M=1.055·10^-7 rad/s=0.5225º/día

Cálculos similares se realizan para obtener la velocidad angular de la Tierra ω_T en su órbita circular alrededor del Sol.

Si queremos que el viaje de la nave espacial entre la Tierra y Marte se realice en T=3 años=36 meses=1080 días. De la fórmula del tiempo T de viaje, obtenemos el valor del ángulo Ψ=88.2º.

El desplazamiento angular de la nave espacial es θ_f=13.3 rad=761º

Si la posición inicial (en el instante t=0) del planeta Marte es φ_0M, su posición cuando llega la nave espacial a las proximidades de su órbita circular, al cabo de un tiempo T es

φ_M=φ_0M+ω_MT

La nave espacial parte de la Tierra en el instante t=0, cuando su posición es φ_0T

Para llegar a la órbita de Marte, la nave se desplaza un ángulo θ_f. Su posición angular final será φ_0T+ θ_f

Para que la posición de la nave espacial y de Marte coincidan se tiene que cumplir la igualdad

φ_0T+ θ_f=φ_0M+ω_MT

La diferencia entre las posiciones angulares de la Tierra y de Marte en el momento del lanzamiento de la nave espacial (t=0) deberá ser de

φ_0T - φ_0M =ω_MT- θ_f
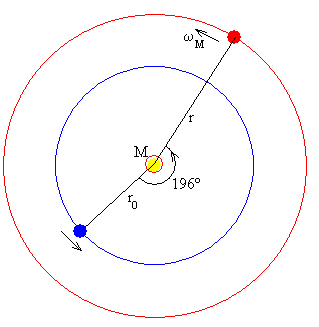
φ_0T - φ_0M =0.5225·1080-761=-196.6º

En la figura, se muestra las posiciones de la Tierra y Marte en el momento de partida de la nave espacial para un viaje de 3 años.

Actividades

Se introduce

• El tiempo de viaje de la nave espacial entre la Tierra y Marte, en meses (30 días), actuando en la barra de desplazamiento titulada Tiempo de viaje.

Se pulsa el botón titulado Nuevo

Se calcula el intervalo angular (φ_0T - φ_0M) entre las posiciones de la Tierra y de Marte en el momento de la partida de la nave espacial, tal como se ha hecho en el ejemplo.

Se pulsa el botón titulado Lanzar.

Si la nave no llega a Marte, se pulsa el botón titulado Nuevo y se vuelve a intentar

En la parte derecha del applet, se nos proporciona los valores del tiempo (en días), la posición angular y la velocidad de los tres cuerpos: la nave espacial, la Tierra y Marte.

Observamos que la nave espacial parte de las proximidades de la Tierra con su misma velocidad orbital y llega a las proximidades de Marte con su misma velocidad orbital. 

KeplerApplet2 aparecerá en un explorador compatible con JDK 1.1.

Referencias

Bacon R. H. Logarithmic spiral: An ideal trajectory for interplanetary vehicle with engines of low sustained thrust. Am. J. Phys. 27 (1959), pp. 164-165.

Curso Interactivo de Física en Internet © Ángel Franco García