Regresión lineal

En esta página, se describe el procedimiento de ajuste de los datos experimentales a una línea recta denominado regresión lineal, que se usa en el laboratorio en varias situaciones:

Para calcular la velocidad en una experiencia de movimiento rectilíneo
Para calcular la constante elástica de un muelle, colocando pesas en un platillo que cuelga de su extremo libre y midiendo la deformación del muelle
etc.

El programa interactivo al final de esta página, está diseñado para que sea usado, en el Laboratorio de Física para cualquier experiencia que lo requiera. Nos proporciona los valores de:

La pendiente a de la recta de regresión y el error cometido Δa
La ordenada en el origen b
El índice de correlación r. Este índice mide el grado de ajuste de los datos experimentales a la recta

Descripción

Supongamos que estamos midiendo la posición de un móvil en función del tiempo en un movimiento rectilíneo. Si el móvil está libre de fuerzas, esperamos que la relación entre la posición del móvil y el tiempo sea lineal x=x₀+vt. Donde x₀ es la posición del móvil en el instante t=0.

Si medimos las posiciones del móvil x₁ y x₂ en los instantes t₁ y t₂, obtenemos un sistema de dos ecuaciones con dos incógnitas de las que podemos determinar las cantidades desconocidas x₀ y v. Ahora bien, esta afirmación solamente es cierta en un experimento ideal libre de errores.

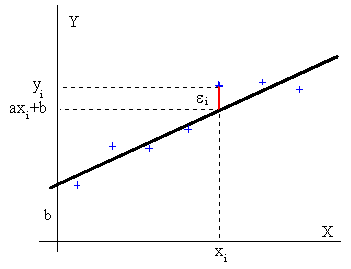
Si efectuamos n medidas de la posición del móvil, el aspecto de la representación gráfica de nuestras medidas puede ser parecido al de la figura más abajo, los puntos de color azul representan los datos experimentales. La relación entre las ordenadas y y las abscisas x de dichos puntos es solamente aproximada, debido a los errores de cada una de las medidas.

Si tomamos únicamente dos puntos para definir la recta el resultado tendría un importante error. Para una mejor estimación de la recta y por tanto, de las magnitudes buscadas, se deberán utilizar las n medidas tomadas.

Supongamos una magnitud física y, relacionada con otra x, mediante la función y=ax+b. Una recta de pendiente a cuya ordenada en el origen es b. Las desviaciones εde los valores de y, véase la figura, serán

ε₁=y₁-(ax₁+b)
ε₂=y₂-(ax₂+b)
...................
ε_i=y_i-(ax_i+b)
...................
ε_n=y_n-(ax_n+b)

Sea E(a,b) la suma de los cuadrados de todas estas desviaciones

E(a,b)=(y₁-ax₁-b)²+(y₂-ax₂-b)²+...(y_i-ax_i-b)²+...+(y_n-ax_n-b)²

$E (a, b) = \sum_{1}^{n} {(y_{i} - a x_{i} - b)}^{2}$

Los valores que minimizan a E(a,b) son aquellos para los que

$\frac{\partial E}{\partial a} = 0 \frac{\partial E}{\partial b} = 0$

Se obtiene así, un sistema de dos ecuaciones con dos incógnitas a y b cuya solución es

$a = \frac{n \sum_{1}^{n} x_{i} y_{i} - (\sum_{1}^{n} x_{i}) (\sum_{1}^{n} y_{i})}{n \sum_{1}^{n} x_{i}^{2} - {(\sum_{1}^{n} x_{i})}^{2}} b = \frac{\sum_{1}^{n} y_{i} - a \sum_{1}^{n} x_{i}}{n}$

Expresiones más elaboradas nos permiten determinar el error de a, Δa y el error de b, Δb

$\begin{array}{l} Δ a = \frac{\sqrt{n} \cdot σ}{\sqrt{n \sum_{1}^{n} x_{i}^{2} - {(\sum_{1}^{n} x_{i})}^{2}}} σ = \sqrt{\frac{\sum_{1}^{n} {(y_{i} - a x_{i} - b)}^{2}}{n - 2}} \\ Δ b = Δ a \cdot \sqrt{\frac{\sum_{1}^{n} x_{i}^{2}}{n}} \end{array}$

La pendiente de la recta se escribirá a±Δa, y la ordenada en el origen b±Δb. Véase las reglas para expresar una medida y su error de una magnitud.

El coeficiente de correlación es otro parámetro para el estudio de una distribución bidimensional, que nos indica el grado de dependencia entre las variables X e Y. El coeficiente de correlación r es un número que se obtiene mediante la fórmula.

$r = \frac{\sum_{1}^{n} (x_{i} - < x >) (y_{i} - < y >)}{\sqrt{\sum_{1}^{n} {(x_{i} - < x >)}^{2}} \sqrt{\sum_{1}^{n} {(y_{i} - < y >)}^{2}}}$

El coeficiente de correlación puede valer cualquier número comprendido entre -1 y +1.

Cuando r=1, la correlación lineal es perfecta, directa.
Cuando r=-1, la correlación lineal es perfecta, inversa
Cuando r=0, no existe correlación alguna, independencia total de los valores X e Y

Ejemplo

Un vehículo que se mueve supuestamente con velocidad constante. Los datos de las medidas del tiempo en cuatro posiciones separadas 900 m son las siguientes

Tiempo t (s)	Posición x (m)
17.6	0
40.4	900
67.7	1800
90.1	2700

Ajustar los datos a la línea recta

x=x₀+vt

y estimar el mejor valor de la velocidad v aplicando el procedimiento de mínimos cuadrados

Introduciendo los datos en el programa interactivo, la pendiente es a=36.71 y el error de la pendiente Δa=1.001. La velocidad se escribe (véase la página Errores en las medidas)

v=37±1 m/s

stokesApplet aparecerá en un explorador compatible con JDK 1.1.