Anterior

Procedimiento numérico

En esta página, se utilizan los siguienets procedimientos numéricos: el método de Montecarlo, y la integral definida por el método de Simpson.

Supondremos que sobre la pantalla hay detectores de anchura Δx. La probabilidad de que un fotón impacte en un detector (en color rojo) situado en la posición x es proporcional al área bajo la curva de la intensidad I, debida a la difracción de la luz por la rendija de anchura b, el área sombreada de color azul claro.

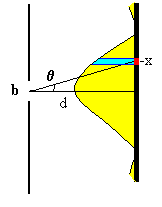
p(x)=c ∫ x−Δx/2 x+Δx/2 sin⁡ 2 u u 2 dx   u= π bsin⁡θ λ   sin⁡θ= x x 2 + d 2

La constante c se determina de modo que la suma de todas las probabilidades p(x) debe ser la unidad

1=c ∫ −∞ ∞ sin⁡ 2 u u 2 dx 

public class Difraccion {
	 double[] prob;       //array de probabilidades en cada detector
	 double d;		//distancia de la rendija a la pantalla
	 double r;		
//apertura :relación anchura de la rendija/longitud de onda
      int N;   		     //número de detectores
      double area;	     //área bajo la curva de la intensidad
      static final int INFINITO=24;
//generador de números aleatorios
     Random rnd=new Random();

  public Difraccion(int _N, double d, double r) {
//N es un número par
//el número de detectores es impar de 0 a N ambos inclusive
//N/2 es el detector central
	this.N=_N;
	if (_N%2==1) 	this.N=_N+1;
	this.d=d;
	this.r=r;
	prob=new double[N+1];
	area=0.0;
//cálculo de los elementos de los arrays
	if(N/2<INFINITO){
		double probAux[]= new double[INFINITO];

		probAux[0]=integral(0.0, 0.5, 10);
		for(int i=1; i<INFINITO; i++){
			probAux[i]=integral(i-1+0.5, i+0.5, 20);
          }
		for(int i=0; i<INFINITO; i++){
			area+=2*probAux[i];
          }
		prob[N/2]=2*probAux[0]/area;
		for(int i=0; i<N/2; i++){
			prob[i]=prob[N-i]=probAux[N/2-i]/area;
          }
//probabilidad acumulada
		for(int i=1; i<=N; i++){
			prob[i]+=prob[i-1];
          }
	}
  }

double f(double x) {
	double u=Math.PI*r*x/Math.sqrt(x*x+d*d);
//límite de sen(x)/x cuando x tiende a cero
	if(u==0){
		return 1;
     }
	double y=(Math.sin(u)*Math.sin(u))/(u*u);
	return y;
}
//método de Simpson
double integral(double a, double b, int n){
	//n debe de ser par
	double h=(b-a)/n;
	double s=f(a)+f(b)+4*f(b-h);
	for(int i=1; i<n-2; i+=2){
		s=s+4*f(a+i*h)+2*f(a+(i+1)*h);
     }
	return s*h/3;
}

int sorteo(){
	//número aleatorio comprendido entre 0 y 1
     double azar=rnd.nextDouble();
	for(int i=0; i<=N; i++){
		if(azar<prob[i]){
			return i;    //dentro de la pantalla
          }
     }
	return (N+1);	//fuera de la pantalla
 }
}
Anterior