La difracción de micropartículas
La experiencia nos enseña que al lanzar una moneda no podemos
predecir de antemano si saldrá cara o cruz, pero cuando lanzamos varias monedas a la vez
o una repetidamente obtenemos, aproximadamente, la mitad cara y la mitad cruz. Decimos
entonces, que la frecuencia con que aparece un resultado es aproximadamente 1/2, y
constataremos que es tanto más próximo a 1/2 cuanto mayor sea el número de
lanzamientos.
Realizando la operación mental de paso al límite, (cuando el número de experiencias es
infinito) diremos que la probabilidad de obtener un resultado (cara o
cruz) es 1/2.
En la vida ordinaria es corriente la identificación de los términos frecuencia y probabilidad, aún cuando el número de experiencias sea reducido, e incluso con una única experiencia.
La conducta de una partícula en el dominio cuántico es esencialmente aleatoria. Sin embargo, es predecible el comportamiento medio de un número muy grande de partículas idénticas.
El objetivo del programa interactivo, es el de comprobar que el concepto de trayectoria de una partícula en Mecánica Cuántica carece de sentido y se ha de sustituir por el concepto de probabilidad mayor o menor de encontrar una partícula en cierta región del espacio.
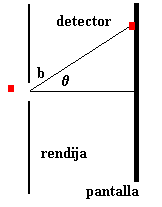
Para ello, se hacen pasar un conjunto de micropartícula (fotón, electrón, etc.) idénticas a través de una rendija estrecha. Sobre una pantalla paralela a la rendija hay situados un conjunto de detectores. Un diagrama de barras nos va indicando los registros de cada contador a medida que las partículas van pasando por la rendija.
Difracción de micropartículas
Consideremos un frente de onda plano que llega a una rendija estrecha. Supongamos que la pantalla está lo suficientemente alejada en comparación con la anchura de la rendija. Se observa sobre la pantalla un conjunto de franjas claras y oscuras que corresponden a los máximos y mínimos de la difracción de la luz por la rendija. A esta situación se la denomina difracción Fraunhofer. Las posiciones de los mínimos están dados por la ecuación
b sinθ =nλ
donde λ es la longitud de onda, b la anchura de la rendija y n un número entero. El valor de n=0 corresponde al máximo central. La intensidad viene dada por la expresión
dicha función tiene un máximo para u=0, y ceros o mínimos para u=nπ
 |
La difracción de una onda luminosa cuando pasa a través de una rendija corresponde a un efecto colectivo de un número muy grande de fotones que inciden sobre la rendija. Cuanto mayor es la intensidad en la posición del detector, mayor es el número de fotones que registra. Por tanto, la probabilidad de que un detector registre un fotón es proporcional a la intensidad de la onda luminosa en dicho lugar. |
Cuando se difractan micropartículas, tal como se simula en el programa, se puede comprobar que:
- Las ondas de de Broglie no tiene nada que ver con las ondas clásicas ya que el paso de una micropartícula a través de la rendija no da lugar al diagrama de difracción de una onda clásica.
- No tiene sentido hablar de trayectoria de una micropartícula sino, de la mayor o menor probabilidad que tendrá la micropartícula de ser registrada por un determinado detector.
- Se obtiene la función que describe la intensidad de la difracción en la pantalla, cuando pasan a través de la rendija un número muy grande de micropartículas.
Actividades
Se introduce
- un número que indica la relación entre la anchura de la rendija y la longitud de onda.
Se pulsa en el botón titulado Empieza.
Las micropartículas van pasando por la rendija una a una. Un detector situado en la pantalla registra las micropartículas. Un diagrama de barras de color azul situado sobre cada uno de los detectores señala el número de partículas registrada por cada detector.
Se pulsa en el botón Pausa para parar momentáneamente la experiencia, y volver a pulsar en el mismo botón titulado ahora Continua, para reanudarla. Se pulsa varias veces en el botón Paso, para observar la conducta individual de cada partícula, su lugar de impacto. Pulsar en el botón Continua para reanudar el experimento.
Observar que el lugar de impacto de una micropartícula sobre la pantalla no está determinado. Pero tiene mayor probabilidad de estar en la región que corresponde al máximo central de la difracción, y menor probabilidad en las regiones que corresponden a los mínimos de intensidad.
Observar que cuando se difracta un número muy grande de micropartículas, el diagrama de barras se ajusta a la curva continua que predice la difracción Fraunhofer.
Principio de incertidumbre
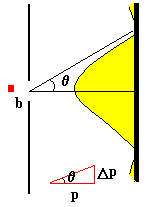Cuando una micropartícula atraviesa la rendija, su posición está indeterminada por
la anchura de la rendija, Δx=b. La dirección de su
velocidad (o su momento lineal) no está unívocamente determinado, sino que varía para
la mayoría de los casos entre +θ y -θ. Por tanto, la incertidumbre en el momento lineal tal como se
ve en la figura es Δp=p·sinθ
El ángulo θ corresponde al primer mínimo de difracción.
Δx·sinθ=λ
Introduciendo la relación de De Broglie λ=h/p en esta última ecuación, obtenemos
Cuanto más angosta es la rendija, menor es la indeterminación Δx=b en la posición de la micropartícula, y mayor es la indeterminación en la dirección de la velocidad, es decir, mayor es el ángulo θ que forma el primer mínimo con la horizontal.
La relación es la óptima entre las indeterminaciones Δx y Δp de la posición x y del momento lineal p de la micropartícula. En la mayoría de los casos, la posición y el momento lineal se conocen con menor precisión, de modo que podemos escribir
Este resultado, se denomina Principio de Incertidumbre de Heisenberg que se enuncia del siguiente modo: es imposible conocer simultáneamente y con exactitud la posición y el momento lineal de una partícula.