Movimiento de un vehículo propulsado por los proyectiles disparados

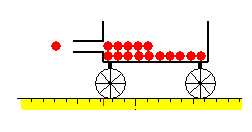Consideremos un vehículo de masa M (un vagón) que se mueve sobre dos raíles horizontales sin rozamiento. El vehículo dispone de un cañón que dispara proyectiles de masa m paralelamente a los raíles y con velocidad u medida respecto al vehículo.

Sobre el vehículo se disponen N proyectiles que se disparan consecutivamente. Calcularemos la velocidad final del vehículo v_f una vez que se hayan disparado todos los proyectiles.

Descripción

La masa del vehículo vacío es M. Cuando hay n proyectiles sobre el vehículo su masa es M+n·m y su velocidad es v_n. Se dispara un proyectil y la masa del vehículo disminuye a M+(n-1)m y su velocidad se incrementa a v_n_-1.

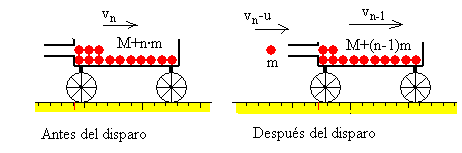
Aplicando el principio de conservación del momento lineal al sistema aislado formado por el vehículo y los proyectiles, relacionamos v_n_-1y v_n

El proyectil es disparado con velocidad -u respecto del vehículo o bien, con velocidad -u+v_n respecto a Tierra

El momento lineal antes del disparo es

p_i=(M+n·m)v_n

El momento lineal después del disparo es

p_f=(M+(n-1)m)·v_n_-1+m(-u+v_n)

$p_{i} = p_{f} v_{n - 1} = v_{n} + \frac{m u}{(M + (n - 1) m)} = v_{n} + \frac{u}{a + n} a = \frac{M}{m} - 1$

El trabajo de las fuerzas internas se invierte en cambiar la energía cinética del sistema formado por el vehículo y el proyectil disparado.

$\begin{array}{l} Δ E_{k} = \frac{1}{2} (M + (n - 1) m) v_{n - 1}^{2} + \frac{1}{2} m {(- u + v_{n})}^{2} - \frac{1}{2} (M + n m) v_{n}^{2} = \\ \frac{1}{2} m u^{2} + \frac{1}{2} m u^{2} (\frac{1}{a + n}) \end{array}$

Disparos consecutivos

La velocidad inicial v_N=0, cuando todos los proyectiles están sobre el vehículo.

Se dispara el primer proyectil

La velocidad del proyectil es

–u

La velocidad del vehículo es

$v_{N - 1} = 0 + \frac{u}{a + N}$

El trabajo de las fuerzas internas es

$Δ E_{1} = \frac{1}{2} m u^{2} + \frac{1}{2} m u^{2} \frac{1}{a + N}$

Se dispara el segundo proyectil

La velocidad del proyectil es

$- u + v_{N - 1} = - u + \frac{u}{a + N}$

La velocidad del vehículo es

$v_{N - 2} = v_{N - 1} + \frac{u}{a + N - 1} = \frac{u}{a + N - 1} + \frac{u}{a + N} = \sum_{i = N - 1}^{N} \frac{u}{a + i}$

El trabajo de las fuerzas internas es

$Δ E_{2} = \frac{1}{2} m u^{2} + \frac{1}{2} m u^{2} (\frac{1}{a + N - 1})$

Se dispara el tercer proyectil

La velocidad del proyectil es

$- u + v_{N - 2} = - u + \frac{u}{a + N - 1} + \frac{u}{a + N}$

La velocidad del vehículo es

$v_{N - 3} = v_{N - 2} + \frac{u}{a + N - 2} = \frac{u}{a + N - 2} + \frac{u}{a + N - 1} + \frac{u}{a + N} = \sum_{i = N - 2}^{N} \frac{u}{a + i}$

El trabajo de las fuerzas internas es

$Δ E_{3} = \frac{1}{2} m u^{2} + \frac{1}{2} m u^{2} (\frac{1}{a + N - 2})$

Se dispara el último proyectil

La velocidad del proyectil es

$- u + v_{N - N + 1} = - u + \sum_{i = 2}^{N} \frac{u}{a + i}$

La velocidad final del vehículo es

$v_{N - N} = v_{f} = \sum_{i = 1}^{N} \frac{u}{a + i}$

El trabajo de las fuerzas internas es

$Δ E_{N} = \frac{1}{2} m u^{2} + \frac{1}{2} m u^{2} (\frac{1}{a + 1})$

Trabajo de las fuerzas internas

La energía cinética final del sistema formado por el vehículo de masa M y los N proyectiles disparados es

$E_{k f} = \frac{1}{2} M v_{N - N}^{2} + \frac{1}{2} m {u^{2} + {(- u + v_{N - 1})}^{2} + {(- u + v_{N - 2})}^{2} + ... + {(- u + v_{N - N + 1})}^{2}}$

Esta es la suma de los trabajos realizados por las fuerzas internas en cada disparo

$E_{k f} = Δ E_{1} + Δ E_{2} + ... Δ E_{n} = N \frac{1}{2} m u^{2} + \frac{1}{2} m u^{2} \sum_{i = 1}^{N} \frac{1}{a + i}$

Ejemplo 1:

Masa del vehículo vacío M=20 kg
Masa del proyectil m=1 kg
Velocidad de disparo del proyectil respecto del vehículo u=10 m/s
Número de proyectiles N=4.

El vehículo de masa M+N·m=24 kg parte del reposo

Después del disparo	Velocidad del proyectil	Velocidad del vehículo (masa)	Trabajo de las fuerzas internas
1º	-10	0.4348 (23)	52.17
2º	-9.5652	0.8893 (22)	52.27
3º	-9.1107	1.3655 (21)	52.38
4º	-8.6345	1.8655 (20)	52.5
Total			209.32

El trabajo de las fuerzas internas es igual a la diferencia entre la energía cinética después del disparo del proyectil y del vehículo y la energía cinética del vehículo antes del disparo. Por ejemplo, en el segundo disparo

$Δ E_{2} = \frac{1}{2} 1 \cdot {9.5652}^{2} + \frac{1}{2} 22 \cdot {0.8893}^{2} - \frac{1}{2} 23 \cdot {0.4348}^{2} = 52.27$

Energía cinética final del sistema es la suma de la energía cinética de los cuatro proyectiles y la energía cinética final del vehículo

$\frac{1}{2} 1 (10^{2} + {9.5652}^{2} + {9.1107}^{2} + {8.6345}^{2}) + \frac{1}{2} 20 \cdot {1.8655}^{2} = 209.32 J$

El trabajo de las fuerzas internas es

$4 \cdot \frac{1}{2} 1 \cdot 10^{2} + \frac{1}{2} 1 \cdot 10^{2} (\frac{1}{19 + 1} + \frac{1}{19 + 2} + \frac{1}{19 + 3} + \frac{1}{19 + 4}) = 209.33 J$

Ejemplo 2:

Masa del vehículo vacío M=50 kg
Masa del proyectil m=0.7 kg
Velocidad de disparo del proyectil respecto del vehículo u=10 m/s
Número de proyectiles N=16.

Velocidad final del vehículo

$\begin{array}{l} v_{f} = \sum_{i = 1}^{N} \frac{u}{a + i} a = \frac{M}{m} - 1 = \frac{50}{0.7} - 1 \\ v_{f} = 10 (\frac{1}{a + 1} + \frac{1}{a + 2} + .... + \frac{1}{a + 16}) = 2.0341 \end{array}$

Actividades

Se introduce

La masa M del vehículo vacío, en el control de edición titulado Masa vacío
La masa m del proyectil, en el control de edición titulado Masa bala
El número N de proyectiles, actuando en la barra de desplazamiento titulada Número de balas
Velocidad de disparo del proyectil respecto del vehículose ha fijado en u=10 m/s

Se pulsa el botón titulado Empieza

Los proyectiles se disparan consecutivamente separados un segundo

Se observa el movimiento del vehículo

En la parte superior del applet, se representa la velocidad del vehículo en función del número de disparo.

Cuando se han terminado de disparar todos los proyectiles el vehículo se mueve con velocidad constante.

Referencias

Brun J. L. Motion of a trolley powered by ejecting balls. Eur. J. Phys. 27 (2006) pp. 1357-1362