Movimiento de dos bloques superpuestos (I)
Supongamos un bloque C que está sobre otro bloque B. El bloque C está unido por una cuerda que pasa por una polea a un bloque A, tal como se muestra en la figura.
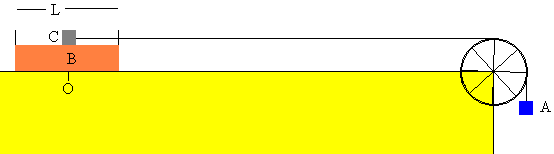
Se deja caer el bloque A y se observa el movimiento del bloque B sobre el plano horizontal y del bloque C sobre el bloque B.
El bloque B de longitud L dispone de dos topes situados en sus extremos, que hacen que cuando el bloque C llegue a dichos extremos el bloque B y el C se muevan con la misma velocidad.
Supondremos que la polea tiene masa despreciable de modo que la tensión de la cuerda es la misma en todos sus puntos. Supondremos también que los coeficientes estático y cinético de rozamiento entre las superficies en contacto tienen el mismo valor. El coeficiente de rozamiento entre el bloque C y el bloque B sobre el que desliza vale μBC. El coeficiente entre el bloque B y el plano horizontal sobre el que desliza vale μB
Descripción
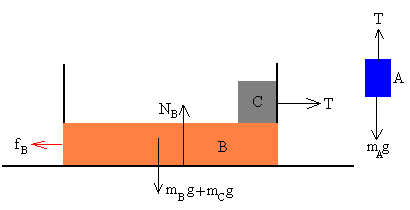
En la figura se muestran las fuerzas sobre los tres bloques
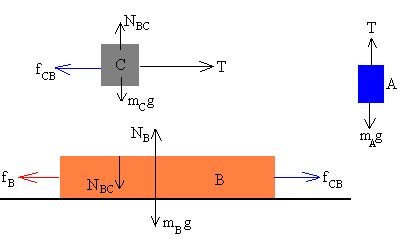
Sobre el bloque A actúan dos fuerzas:
- El peso mAg
- La tensión de la cuerda T
Sobre el bloque C actúan
- El peso mCg
- La tensión de la cuerda T
- La reacción de la superficie sobre la que descansa NBC
- La fuerza de rozamiento que se opone al deslizamiento del bloque sobre dicha superficie fBC
Sobre el bloque B actúan
- El peso mBg
- La reacción de la superficie sobre la que descansa NB
- Por el principio de acción y reacción el bloque B ejerce una fuerza NBC sobre el bloque C y éste ejerce una fuerza igual y de sentido contrario sobre el bloque B
- Del mismo modo, bloque B ejerce una fuerza fBC sobre el bloque C y éste ejerce una fuerza igual y de sentido contrario sobre el bloque B
- La fuerza de rozamiento que se opone al deslizamiento del bloque sobre la superficie horizontal fB
Los bloques están en equilibrio en la dirección vertical de modo que
NBC=mCg
NB=mCg+NBC=(mC+mB)g
El bloque C desliza sobre el bloque B si la fuerza de rozamiento fBC alcanza su valor máximo μBC·NBC= μBC·mCg
El bloque B desliza sobre el plano horizontal si la fuerza de rozamiento fB alcanza su valor máximo μB·NB= μB·(mC+mB)g
Vamos a considerar las distintas situaciones
Equilibrio
- Si mAg < μBC·mCg el bloque C permanece en reposo y la fuerza de rozamiento vale fBC= mAg
- Si fBC< μB·(mC+mB)g el bloque B permanece en reposo y la fuerza de rozamiento fB= fBC
Dinámica
Cuando el bloque A se mueve su aceleración es aA
mAg-T=mAaA
- Si mAg ≥ μBC·mCg el bloque C se mueve y la fuerza de rozamiento entre los bloques B y C alcanza su valor máximo fBC= μBC·mCg
- Cuando fBC≥ μB·(mC+mB)g el bloque B se mueve arrastrado por el bloque C, la fuerza de rozamiento entre el bloque B y el plano horizontal alcanza su valor máximo fB= μB·(mC+mB)g, la aceleración del bloque B es
- Cuando fBC< μB·(mC+mB)g el bloque B no se mueve aB=0 y la fuerza de rozamiento vale fB=μBC·mCg,
- Si mAg < μBC·mCg
-
Si fBC≥ μB·(mC+mB)g, el bloque B se mueve y arrastra consigo al bloque C.
La ecuación del movimiento de los bloques B y C es
T- μB·(mC+mB)g =(mB+mC)aBC
Como la ecuación del movimiento del bloque A es
mAg-T=mAaALa aceleración de los bloques A, B y C es la misma e igual a
- Si fB< μB·(mC+mB)g, todos los bloques permanecen en reposo, la fuerza de rozamiento entre el bloque B y el plano horizontal vale fB=fBC=mAg
La aceleración del bloque C, aC es
T- μBC·mCg=mCaC
Como los bloques A y C están unidos por una cuerda, sus aceleraciones son iguales aC= aA
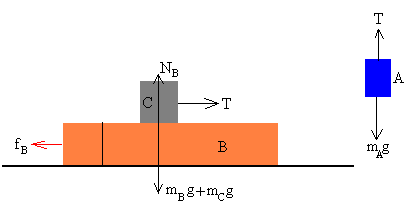
La fuerza de rozamiento entre el bloque C y el bloque B es fBC= mAg, el bloque C queda pegado al bloque B.
Si μB es pequeño, como ocurre en la experiencia de laboratorio, el bloque B es arrastrado por el bloque C.
Si el rozamiento entre las superficies BC es grande, el bloque C queda pegado al bloque B y todos los bloques se mueven con la misma aceleración.
Los bloques parten del reposo y se desplazan horizontalmente, sus posiciones al cabo de un cierto tiempo t son.
Choque
Si aC≠aB el cuerpo C llega al extremo derecho o izquierdo del bloque B. Si L es la longitud del bloque, el tiempo que tarda en llega a dicho extremo es
con velocidades

La velocidad común después del choque es
A partir de este momento las ecuaciones del movimiento del conjunto de los dos bloque B y C y del bloque impulsor A son
mAg-T=mAa
T-μB·(mC+mB)g=(mC+mB)a
Las posiciones posteriores de los bloques B y C son
Ejemplo 1
- Rozamiento: μBC=0.4, μB=0.7
- Masa de los bloques: mA=2, mB=2, mC=1
Se cumple que
mAg ≥ μBC·mCg
La aceleración de los bloques A y C es
La fuerza de rozamiento alcanza su valor máximo fBC= μBC·mCg
Sin embargo, fBC< μB·(mC+mB)g por lo que el cuerpo B permanece en reposo aB=0
Al cabo de un tiempo
el bloque C llega al extremo derecho del bloque B, su velocidad común es
La aceleración del bloque impulsor A y de los bloques B y C a partir de dicho instante es
Los bloques se detienen al cabo de un tiempo Δt=3.88 s, en la posición
xB=1.47 m.
Ejemplo 2
- Rozamiento: μBC=0.7, μB=0.1
- Masa de los bloques: mA=0.8, mB=2, mC=1
Se cumple que
mAg ≥ μBC·mCg
La aceleración de los bloques A y C es
La fuerza de rozamiento alcanza su valor máximo fBC= μBC·mCg
Como, fBC> μB·(mC+mB)g por lo que el cuerpo B se mueve con aceleración aB
Al cabo de un tiempo
el bloque C llega al extremo izquierdo del bloque B, su velocidad común es
La aceleración del bloque impulsor A y de los bloques B y C a partir de dicho instante es
Los bloques continúan su movimiento acelerado
Ejemplo 3
- Rozamiento: μBC=0.7, μB=0.1
- Masa de los bloques: mA=0.4, mB=2, mC=1
Se cumple que mAg < μBC·mCg el bloque C queda pegado al bloque B. La fuerza de rozamiento entre el bloque B y C es fBC= mAg
Como, fBC> μB·(mC+mB)g por lo que el cuerpo B se mueve arrastrando al cuerpo C con aceleración aB
Actividades
Se introduce
- La masa mA del bloque A, en el control de edición titulado Masa A
- La masa mB del bloque B, en el control de edición titulado Masa B
- La masa del bloque C se ha fijado en el valor mC=1 kg
- El coeficiente de rozamiento μBC entre las superficies de los bloques B y C, actuando en la barra de desplazamiento titulada Coef. roza. BC
- El coeficiente de rozamiento μB entre el bloque B y el plano horizontal, actuando en la barra de desplazamiento titulada Coef. roza. B
Se pulsa el botón titulado Empieza
Observamos el movimiento de los bloques B y C, primero separadamente y luego, cuando van juntos una vez que el bloque C haya alcanzado uno de los extremos del bloque B.
En la parte superior del applet, se muestran los datos del tiempo t, y de las aceleración del bloque C, aC y del bloque B, aB.
Referencias
Sullivan P., Novak J., Sancilio P.A block dragging a cart. The Physics Teacher 44, February 2006, pp. 114-116