• Inicio
• Dinámica
• Sistemas de partículas

El operario ejerce una fuerza constante

Tenemos en este caso, un sistema de dos partículas bajo la acción de dos fuerzas externas, la fuerza F que ejerce el operario y la fuerza de rozamiento F_r que ejerce el suelo sobre la caja y una fuerza de interacción mutua, que es la que ejerce el muelle elástico deformado que une ambos cuerpos. En la figura, se muestra la situación inicial

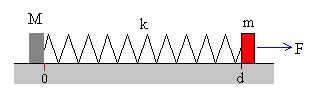
Supongamos que un operario de masa m tira del extremo del muelle elástico de constante k con una fuerza constante F. El otro extremo del muelle elástico está unido a una caja de masa M. Estudiaremos la dinámica del sistema formado por ambos cuerpos. El planteamiento del problema tiene dos partes:

• Cuando la caja está en reposo en la posición x₀

• Cuando la caja está en movimiento

La caja está en resposo

En un determinado instante t, el operario se encuentra en la posición y.

Las fuerzas sobre el operario son:

• La fuerza constante F

• La fuerza que ejerce el muelle elástico deformado k(y-x₀-d)

Como la caja está en reposo, la fuerza de rozamiento F_r se equilibra con la fuerza que ejerce el muelle elástico.

La ecuación del movimiento del operario es

${\displaystyle m\frac{d^{2}y}{d{t}^2}=F-k(y-x_0-d)}$

cuya solución es

${\displaystyle \begin{array}{l}y=A\sin (\omega t+\varphi )+\frac{F}{m{\omega }^2}+x_0+d{\omega }^2=\frac{k}{m}\\ v_y=\frac{dy}{dt}=A\omega \cos (\omega t+\varphi )\end{array}}$

La amplitud y la fase inicial se determinan a partir de las condiciones iniciales: En el instante t=0, el operario parte de la posición y₀ con velocidad v_0y

${\displaystyle A\sin \varphi =y_0-\frac{F}{m{\omega }^2}-x_0-dA\cos \varphi =\frac{v_{0y}}{\omega }}$

En el instante t_f en el que la fuerza de rozamiento alcanza su valor máximo μ_sMg, la caja empieza a deslizar.

k(y-x₀-d)= μ_sMg

La posición y_f y velocidad final v_fy del operario son

${\displaystyle \begin{array}{l}A\sin (\omega t_f+\varphi )=\frac{{\mu }_{s}Mg-F}{m{\omega }^2}\\ y_f=\frac{{\mu }_{s}Mg}{m{\omega }^2}+x_0+d{v}_{fy}=A\omega \text{cos}(\omega t_f+\varphi )\end{array}}$

Cuando empujamos una caja de masa M, la fuerza F mínima necesaria para que empiece a deslizar es  F= μ_sMg. Sin embargo, si tiramos de la caja por medio de un muelle, la fuerza F mínima necesaria es la mitad F= μ_sMg/2, como vamos a demostrar a continuación:

La caja parte de la posición x₀=0, y el operario de la posición y₀=d, con velocidad v_0y=0

Con estas condiciones iniciales, la amplitud A y la fase inicial φ valen, respectivamente

A=F/(mω²) y φ=3π/2

Para que la caja empiece a deslizar tiene que existir la raíz t_f de la ecuación

${\displaystyle A\sin (\omega t_f+\varphi )=\frac{{\mu }_{s}Mg-F}{m{\omega }^2}}$

es decir

${\displaystyle \left|\frac{{\mu }_{s}Mg-F}{m{\omega }^{2}A}\right|=\left|\frac{{\mu }_{s}Mg-F}{F}\right|\le 1}$

El valor mínimo de F= μ_sMg/2

Si F< μ_sMg/2, la caja permanece en reposo y el operario describe un M.A.S. de amplitud A y frecuencia angular ω. La posición de equilibrio (la fuerza sobre le operario es nula) se encuentra en $d+\frac{F}{m{\omega }^2}$

La figura muestra la trayectoria del operario en el espacio de las fases x-v, la caja está en reposo en el origen. El operario alcanza una velocidad máxima cuando pasa  por la posición de equilibrio y una velocidad mínima en d y en $d+\frac{2F}{m{\omega }^2}$ .

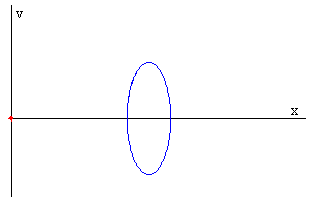
Datos: F=3 N, M=1 kg, k=8 N/m, μ_s=0.75

 

La caja empieza a deslizar

En un determinado instante t, el operario se encuentra en la posición y y la caja se encuentra en la posición x.

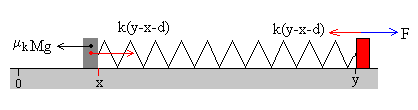
Las fuerzas sobre el operario son:

• La fuerza constante F

• La fuerza que ejerce el muelle elástico deformado k(y-x-d)

Las fuerzas sobre la caja son:

• La fuerza que ejerce el muelle k(y-x-d)

• La fuerza de rozamiento cinético F_r= μ_kMg

Las ecuaciones del movimiento de la caja y del operario son, respectivamente

${\displaystyle \begin{array}{l}M\frac{d^{2}x}{d{t}^2}=k(y-x-d)-{\mu }_{k}Mg\\ m\frac{d^{2}y}{d{t}^2}=F-k(y-x-d)\end{array}}$

Movimiento relativo

Multiplicamos la primera ecuación por m y la segunda por M y las restamos

${\displaystyle mM\left(\frac{d^{2}y}{d{t}^2}-\frac{d^{2}x}{d{t}^2}\right)=MF+{\mu }_{k}Mmg-k(M+m)(y-x-d)}$

Llamando  ξ=y-x-d

${\displaystyle \frac{d^2\xi }{d{t}^2}+\frac{k(M+m)}{Mm}\xi =\frac{MF+{\mu }_{k}Mmg}{mM}}$

La solución de esta ecuación diferencial es

${\displaystyle \xi =B\sin (\Omega t+\phi )+\frac{F/m+{\mu }_{k}g}{{\Omega }^2}}$

Movimiento del centro de masas

La posición del centro de masas es

${\displaystyle z=\frac{Mx+my}{M+m}}$

Sumando las dos ecuaciones diferenciales

${\displaystyle \begin{array}{l}m\frac{d^{2}y}{d{t}^2}+M\frac{d^{2}x}{d{t}^2}=F-{\mu }_{k}Mg\\ \frac{d^{2}z}{d{t}^2}=\frac{F-{\mu }_{k}Mg}{m+M}\end{array}}$

El movimiento del centro de masas depende solamente de las fuerzas externas y es uniformemente acelerado

${\displaystyle \begin{array}{l}{v}_z=v_{0z}+\frac{F-{\mu }_{k}Mg}{m+M}t\\ z=z_0+v_{0z}t+\frac{1}{2}\frac{F-{\mu }_{k}Mg}{m+M}{t}^2\end{array}}$

• Cuando F> μ_kMg, el centro de masas se acelera,

• Cuando F< μ_kMg el centro de masas decelera, su velocidad disminuye

• Cuando F= μ_kMg,  el centro de masas se mueve con velocidad constante

Posición de las partículas del sistema

Conocido la ecuación del movimiento relativo de las dos partículas ξ(t) y la posición del centro de masas z(t), podemos despejar la posición x de la caja y la posición y del operario.

y-x-d= ξ(t)
my+Mx=(m+M)z(t)

${\displaystyle y=z(t)+\frac{M}{m+M}\left(\xi (t)+d\right)x=z(t)-\frac{m}{m+M}\left(\xi (t)+d\right)}$

La amplitud B, la fase φ,, la posición inicial z₀ y la velocidad inicial v_0z del centro de masas se determinan a partir de las condiciones iniciales.

En el instante t=0, la posición de la caja es x₀ y parte del reposo v_0x=0

La posición  y₀ y velocidad v_0y del operario son las finales de la etapa anterior:

${\displaystyle \begin{array}{l}A\sin (\omega t_f+\varphi )=\frac{{\mu }_{s}Mg-F}{m{\omega }^2}\\ y_0=\frac{{\mu }_{s}Mg}{m{\omega }^2}+x_0+d{v}_{0y}=A\omega \text{cos}(\omega t_f+\varphi )\end{array}}$

La posición inicial y la velocidad inicial del centro de masas son

${\displaystyle \begin{array}{l}{z}_0=\frac{m{y}_0+M{x}_0}{m+M}{v}_{0z}=\frac{m{v}_{0y}}{m+M}\\ y_0-x_0-d=B\sin \phi +\frac{F/m+{\mu }_{k}g}{{\Omega }^2}{v}_{0y}=B\Omega \cos \phi \\ B\sin \phi =\frac{{\mu }_{s}Mg}{m{\omega }^2}-\frac{F/m+{\mu }_{k}g}{{\Omega }^2}B\cos \phi =\frac{A\cos (\omega t_f+\varphi )}{\Omega }\end{array}}$

La velocidad de la caja en esta etapa es

${\displaystyle \frac{dx}{dt}=v_{0z}+\frac{F-{\mu }_{k}Mg}{m+M}t-\frac{m}{m+M}B\Omega \cos (\Omega t+\phi )}$

La velocidad de la caja se hace cero en un instante t raíz de la ecuación trascendente

${\displaystyle v_{0z}+\frac{F-{\mu }_{k}Mg}{m+M}t-\frac{m}{m+M}B\Omega \cos (\Omega t+\phi )=0}$

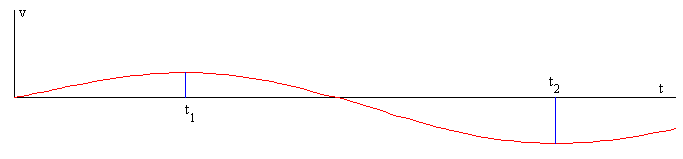
En la figura, se muestra la velocidad de la caja en función del tiempo. La raíz buscada t está entre el instante t₁ para el que la velocidad es máxima y el instante t₂ para el cual la velocidad es mínima. El máximo y el mínimo son las raíces de la ecuación

${\displaystyle \frac{F-{\mu }_{k}Mg}{m+M}+\frac{m}{m+M}B{\Omega }^2\sin (\Omega t+\phi )=0}$

La figura muestra la trayectoria en el espacio de las fases x-v, de la caja (en color rojo) y del operario (en color azul) cuando el c.m. decelera F< μ_kMg, su velocidad se hace cero al cabo de cierto tiempo y el sistema de partículas no puede moverse más allá de cierta distancia.

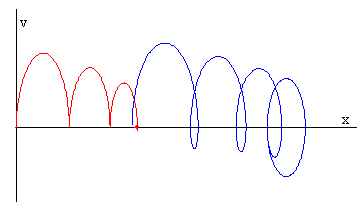
Datos: F=4.5 N, M=1 kg, m=1 kg, k=8 N/m, μ_s=0.75, μ_k=0.5

La figura muestra la trayectoria en el espacio de las fases x-v, de la caja (en color rojo) y del operario (en color azul) cuando el c.m. se mueve con velocidad constante F=μ_kMg.

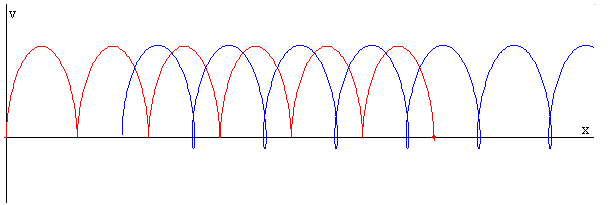
Datos: F=4.9 N, M=1 kg, m=1 kg, k=8 N/m, μ_s=0.75, μ_k=0.5

La figura muestra la trayectoria en el espacio de las fases x-v, de la caja (en color rojo) y del operario (en color azul) cuando el c.m. acelera F>μ_kMg.

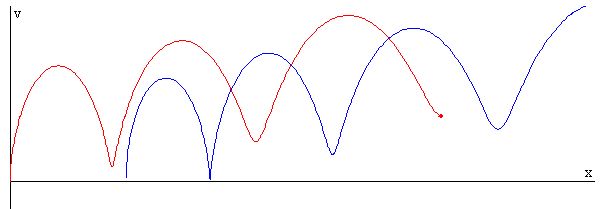
Datos: F=5.5 N, M=1 kg, m=1 kg, k=8 N/m, μ_s=0.75, μ_k=0.5

Balance energético

La energía del sistema de partículas es la suma de la energía cinética de las dos partículas y de la energía potencial de interacción entre ambas.

${\displaystyle U=\frac{1}{2}m{v}_y^2+\frac{1}{2}M{v}_x^2+\frac{1}{2}k{\left(y-x-d\right)}^2}$

El trabajo de las fuerzas exteriores

W_ext=F(y-d)- μ_kMgx

modifica la energía del sistema de partículas

W_ext=U-U₀

Actividades

Se introduce

• La fuerza constante F que ejerce el operario, en N, en el control de edición titulado Fuerza

• La masa m del operario, en kg, en el control de edición titulado Masa

• La masa M de la caja se ha fijado en 1 kg

• El coeficiente de rozamiento estático µ_s, actuando en la barra de desplazamiento Coef. estático

• El coeficiente de rozamiento cinético µ_k, actuando en la barra de desplazamiento Coef. cinético. Se debe de cumplir que µ_k≤µ_s

• La constante k en N/m, del muelle elástico, en el control de edición titulado Constante.

Se pulsa el botón titulado Empieza

Los valores críticos de la fuerza F son

• μ_sMg/2, para que la caja empiece a deslizar

• μ_kMg, para que la caja deslice sin detenerse.

El applet simula el movimiento de la caja y del operario, representado por un vehículo, ambos unidos por un muelle elástico.

Se representan mediante flechas, las fuerzas sobre la caja y sobre el operario

En la parte superior, se representa en el espacio de las fases x-v

• En color rojo, la trayectoria de la caja

• En color azul, la trayectoria del operario

En la parte izquierda del applet, se representa el balance energético

La altura de la barra, es el trabajo realizado por la fuerza constante F

• En color azul, la energía cinética del operario

• En color rojo, la energías cinética de la caja.

• En color verde, la energía almacenada en el muelle elástico deformado

• En color negro, el trabajo de la fuerza de rozamiento.

stokesApplet aparecerá en un explorador compatible con JDK 1.1.

Curso Interactivo de Física en Internet © Ángel Franco García