La lluvia que cae en un vagón de ferrocarril

En los cursos de Física General se ilustra la aplicación de la definición de fuerza F=dp/dt con el problema del vagón de ferrocarril que incrementa su masa a razón constante, debido a la lluvia que cae uniformemente.

Cuando no se aplican fuerzas

Se resuelve un problema cuyo enunciado es similar al siguiente:

Un vagón de ferrocarril que está abierto por arriba, se mueve a lo largo de vías rectilíneas con velocidad v₀. En un momento dado, comienza a llover verticalmente, incrementándose la masa del vagón a razón constante de f kg/s. Sabiendo que la masa inicial del vagón es m₀ kg. Calcular

La masa m del vagón en función del tiempo t
La velocidad v del vagón en función del tiempo
La aceleración a
La posición x del móvil en función del tiempo t, si parte del origen
La fuerza F necesaria para que el vagón se mueva con velocidad constante v₀.

La solución del problema es

Masa del vagón

La masa del vagón en el instante t es

m=m₀+f·t

Velocidad del vagón

Como la fuerza sobre el vagón es nula F=0, el momento lineal se mantiene constante.

F=dp/dt, si F=0, p=cte

Al incrementarse la masa del vagón disminuye su velocidad. La velocidad v del vagón en el instante t es

m₀·v₀=(m₀+f·t)·v

$v = \frac{m_{0} v_{0}}{m_{0} + f \cdot t}$

Tenemos una situación equivalente, cuando un cuerpo de masa m₀ que lleva una velocidad inicial v₀ choca inelásticamente con pequeño cuerpo de masa Δm en reposo. La velocidad v₁ después del primer choque es

mv₀=(m+Δm)v₁

Si el cuerpo resultante de masa m₀+Δm se vuelve a encontrar con otro pequeño cuerpo de masa Δm en reposo. La velocidad v₂ después del segundo choque es

m₀v₀=(m₀+Δm)v₁=(m₀+2Δm)v₂.

después de n choques consecutivos, el cuerpo tendrá una masa (m₀+n·Δm), y su velocidad será

$v_{n} = \frac{m_{0} v_{0}}{m_{0} + n \cdot Δ m}$

En la expresión anterior el término f·t es el incremento de la masa del vagón. En ésta, n·Δm es el incremento de la masa del cuerpo como resultado de sus choques inelásticos

La aceleración del vagón es

$a = \frac{d v}{d t} = - \frac{m_{0} v_{0} f}{{(m_{0} + f \cdot t)}^{2}}$

Aunque la fuerza sobre el vagón es cero, la aceleración no es nula.

Posición del vagón

Integrando la expresión de la velocidad obtenemos la posición x del vagón en función del tiempo

$\begin{array}{l} \frac{d x}{d t} = \frac{m_{0} v_{0}}{m_{0} + f \cdot t} \\ \int_{0}^{x} d x = \int_{0}^{t} \frac{m_{0} v_{0}}{m_{0} + f \cdot t} d t x = \frac{m_{0} v_{0}}{f} \ln \frac{m_{0} + f \cdot t}{m_{0}} \end{array}$

Velocidad constante del vagón

Al aumentar su masa m, el vagón disminuye la velocidad v. Para que el vagón se mueva con velocidad constante v₀, es necesario aplicar una fuerza F tal que

$F = \frac{d p}{d t} = \frac{d (m v_{0})}{d t} = \frac{d m}{d t} v_{0} = f \cdot v_{0}$

Cuando se aplican fuerzas.

Vamos a estudiar en este apartado, el movimiento de un vagón cuya masa inicial es m₀ y cuya velocidad inicial es v₀, que incrementa su masa a razón constante de f kg/s. Sobre el vagón se ejerce una fuerza F mediante una máquina de tren conectada al vagón y además, estudiaremos el efecto de la fuerza de rozamiento cuyo coeficiente es μ.

La masa del vagón en el instante t es m=m₀+f·t
Su velocidad es v, y su momento lineal p=(m₀+f·t)v

Las fuerzas que actúan sobre el vagón son:

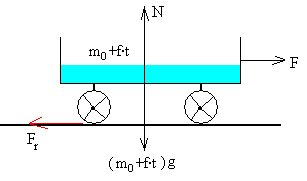
El peso (m₀+f·t)g
La reacción N de las vías, igual y de sentido contrario al peso, N=(m₀+f·t)g
La máquina de tren arrastra el vagón con una fuerza F constante
La fuerza de rozamiento F_r=μ·N= μ·(m₀+f·t)g. La fuerza de rozamiento no es constante y se incrementa con la masa del vagón.

La ecuación del movimiento del vagón es

$\frac{d p}{d t} = F - μ (m_{0} + f \cdot t) g$

En el instante t=0, la velocidad inicial es v₀, y el vagón parte del origen x=0.

$\begin{array}{l} \int_{p_{0}}^{p} d p = \int_{0}^{t} (F - μ m_{0} g - μ g f \cdot t) d t \\ p = p_{0} + (F - μ m_{0} g) t - \frac{1}{2} μ g f \cdot t^{2} \end{array}$

Velocidad del vagón

La velocidad v del vagón en el instante t es

$v = \frac{m_{0} v_{0} + (F - μ m_{0} g) t - μ f g t^{2} / 2}{m_{0} + f \cdot t}$

La velocidad se hace cero cuando el numerador lo sea, es decir, en el instante t, tal que

$t = \frac{(F - μ m_{0} g) + \sqrt{{(F - μ m_{0} g)}^{2} + 2 μ f g m_{0} v_{0}}}{μ f g}$

Si el vagón parte del reposo v₀=0, el tiempo que tarda en pararse es

$t = \frac{2 (F - μ m_{0} g)}{μ f g}$

El tiempo es positivo (el vagón se mueve) si F> μm₀g. (la fuerza de rozamiento inicial)

Posición del vagón

La posición x del vagón en función del tiempo t es

$\int_{0}^{x} d x = \int_{0}^{t} \frac{m_{0} v_{0} + (F - μ m_{0} g) t - μ f g t^{2} / 2}{m_{0} + f \cdot t} d t$

Para resolver la integral, se divide primero el numerador entre el denominador, calculando el cociente y el resto de la división. El resultado final es

$x = - \frac{μ g}{4} t^{2} + \frac{F - μ m_{0} g / 2}{f} t + \frac{m_{0}}{f} (v_{0} - \frac{F - μ m_{0} g / 2}{f}) \ln \frac{m_{0} + f t}{m_{0}}$

Casos particulares

Si F=0 y μ=0, obtenemos

$v = \frac{m_{0} v_{0}}{m_{0} + f \cdot t} x = \frac{m_{0} v_{0}}{f} \ln \frac{m_{0} + f \cdot t}{m_{0}}$

Si F≠0, y μ=0, obtenemos

$v = \frac{m_{0} v_{0} + F t}{m_{0} + f \cdot t} x = \frac{F}{f} t + \frac{m_{0}}{f} (v_{0} - \frac{F}{f}) \ln \frac{m_{0} + f t}{m_{0}}$

La velocidad v se hace constante e igual a v₀ cuando F=f·v₀, entonces x=v₀·t

Ejemplos

Ejemplo1:

Sea F=0, y μ=0

f=0.7 kg/s
v₀=0.1 m/s
m₀=50 kg

La velocidad en el instante t=50 s es

$v = \frac{50 \cdot 0.1}{50 + 0.7 \cdot 40} = 0 .064 m/s x = \frac{50 \cdot 0.1}{0.7} \ln \frac{50 + 0.7 \cdot 40}{50} = 3.18 m$

Ejemplo 2:

Sea μ=0

f=0.7 kg/s
v₀=0.1 m/s
m₀=50 kg

La velocidad v₀ es constante cuando la fuerza F=f·v₀=0.7·0.1=0. 07 N

Cuando F es más pequeña que este valor, el vagón se frena, y cuando es más grande se acelera

Ejemplo 3:

Sea μ=0.1

f=0.7 kg/s
v₀=0 m/s
m₀=50 kg

Introducimos el valor de la fuerza F que sea mayor que la fuerza de rozamiento inicial μm₀g=0.1·50·9.8=49 N

Por ejemplo, F=60 N

Observamos que el vagón parte del reposo, se acelera, hasta que alcanza una velocidad máxima y luego, se decelera hasta que se para. El tiempo que tarda en pararse es

$t = \frac{2 (60 - 49)}{0.1 \cdot 0.7 \cdot 9.8} = 32.07 s$

En este tiempo, el vagón se ha desplazado

$x = - \frac{0.1 \cdot 9.8}{4} {32.07}^{2} + \frac{60 - 49 / 2}{0.7} 32.07 + \frac{50}{0.7} (0 - \frac{60 - 49 / 2}{0.7}) \ln \frac{50 + 0.7 \cdot 32.07}{50} = 31.0 m$

Actividades

Se introduce

La velocidad inicial v₀, en el control de edición titulado Velocidad inicial
La masa inicial del vagón se ha fijado en m₀=50 kg
La fuerza F con la que tira la máquina de tren del vagón, en el control de edición titulado Fuerza.
La razón constante f del incremento de la masa del vagón, actuando en la barra de desplazamiento titulada Flujo
El coeficiente de la fuerza de rozamiento μ, en el control de edición titulado Coef. rozamiento.

Se pulsa el botón titulado Empieza

Se observa el movimiento del vagón arrastrado o no por la máquina según que la fuerza F sea positiva o nula, respectivamente.

La masa del vagón se incrementa con el tiempo, debido a la caída de la lluvia, que se representa por el movimiento vertical de puntos de color azul.

Referencias

Lapidus I. R. Problem: the rain in the plain falls mainly on the train. Am. J. Phys. 53 (7) July 1985, Enunciado pág 644, solución pág 697.