• Inicio
• Dinámica
• Sistemas de masa variable

La gota de lluvia que cae a través de una nube

Una gota de agua de lluvia cae a través de una nube de pequeñas gotitas. A medida que cae, incrementa su masa al chocar inelásticamente con las pequeñas gotitas. El problema consiste en determinar la posición x y velocidad v de la gota en función del tiempo t, conocida la masa inicial m₀, la velocidad inicial v₀ y la altura inicial x₀ en el instante t=0.

 

 

 

 

La masa de la gota

Hemos de hacer una suposición acerca de la forma en que la masa de la gota se incrementa con el tiempo. Si la gota va absorbiendo las pequeñas gotitas que encuentra en su camino, entonces

${\displaystyle \frac{dm}{dt}\propto (\text{área)}\times \text{(velocidad})\propto \pi r^{2}v={\rho }_n\pi r^{2}v=k{m}^{2/3}v}$

• πr² es el área trasversal de la gota supuesta esférica

• ρ_n es la densidad de la niebla,

• v es la velocidad de la gota

• m es la masa de la gota, y ρ_a es la densidad del agua, m=densidad·volumen=ρ_a·(4/3)πr³

El valor de la constante de proporcionalidad k es

${\displaystyle k=\frac{{\rho }_n\pi }{{\left({\rho }_a\frac{4}{3}\pi \right)}^{2/3}}}$

En general, supondremos que la razón del incremento de la masa de la gota con el tiempo es de la forma

${\displaystyle \frac{dm}{dt}=k{m}^{\alpha }v}$

Como la velocidad v=dx/dt

${\displaystyle \frac{dm}{dt}=k{m}^{\alpha }\frac{dx}{dt}}$

Integramos esta ecuación con las condiciones iniciales para x=0, m=m₀

${\displaystyle \begin{array}{l}{\displaystyle \underset{m_0}{\overset{m}{\int }}{m}^{-\alpha }}dm={\displaystyle \underset{0}{\overset{x}{\int }}k·dx}\\ m^{1-\alpha }-m_0^{1-\alpha }=(1-\alpha )kx\\ m={\left((1-\alpha )kx+m_0^{1-\alpha }\right)}^{1/(1-\alpha )}\end{array}}$

Esta ecuación nos proporciona la masa m de la gota en función de la posición x.

Ecuaciones del movimiento

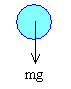Sobre la gota de masa m actúa una única fuerza que es su peso mg. La segunda ley de Newton aplicada a este sistema de masa variable se escribe

${\displaystyle \frac{d(mv)}{dt}=mgm\frac{dv}{dt}+v\frac{dm}{dt}=mg}$

Cuando g=0

Empezaremos por el caso más simple, aquél en el que la aceleración de la gravedad es cero. Podría ser el caso de un objeto que pasase a través de la materia interestelar.

Como la fuerza exterior es nula, el momento lineal se conserva, al aumentar la masa disminuye la velocidad de la gota

m₀v₀=mv

${\displaystyle \frac{dx}{dt}=\frac{m_0{v}_0}{m}=\frac{m_0{v}_0}{{\left((1-\alpha )kx+m_0^{1-\alpha }\right)}^{1/(1-\alpha )}}}$

Integramos

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{x}{\int }}{\left((1-\alpha )kx+m_0^{1-\alpha }\right)}^{1/(1-\alpha )}}dx={\displaystyle \underset{0}{\overset{t}{\int }}{m}_0{v}_{0}dt}\\ \frac{1}{k(2-\alpha )}\left\{{\left((1-\alpha )kx+m_0^{1-\alpha }\right)}^{(2-\alpha )/(1-\alpha )}-m_0^{(2-\alpha )}\right\}=m_0{v}_{0}t\end{array}}$

Expresamos x en función del tiempo t

${\displaystyle x=\frac{1}{k(1-\alpha )m_0^{(-1+\alpha )}}\left\{{\left(k(2-\alpha )m_0^{(-1+\alpha )}{v}_{0}t+1\right)}^{(1-\alpha )/(2-\alpha )}-1\right\}}$

Calculamos ahora la velocidad v en función del tiempo t

${\displaystyle v=\frac{m_0{v}_0}{m}=\frac{m_0{v}_0}{{\left((1-\alpha )kx+m_0^{1-\alpha }\right)}^{1/(1-\alpha )}}=\frac{v_0}{{\left(k(2-\alpha )m_0^{(-1+\alpha )}{v}_{0}t+1\right)}^{1/(2-\alpha )}}}$

Integrando de nuevo, obtenemos la posición x de la gota en función del tiempo t.

${\displaystyle x={\displaystyle \underset{0}{\overset{t}{\int }}\frac{v_0}{{\left(k(2-\alpha )m_0^{(-1+\alpha )}{v}_{0}t+1\right)}^{1/(2-\alpha )}}dt}=\frac{1}{k(1-\alpha )m_0^{(-1+\alpha )}}\left\{{\left(k(2-\alpha )m_0^{(-1+\alpha )}{v}_{0}t+1\right)}^{(1-\alpha )/(2-\alpha )}-1\right\}}$

Cuando α=2/3 las expresiones de la masa m de la gota, la velocidad v y la posición x en función del tiempo t son:

${\displaystyle \begin{array}{l}m={\left(\frac{1}{3}kx+m_0^{1/3}\right)}^3\\ v=\frac{v_0}{{\left(\frac{4}{3}k{m}_0^{-1/3}{v}_{0}t+1\right)}^{3/4}}x=\frac{3m_0^{1/3}}{k}\left\{{\left(\frac{4}{3}k{m}_0^{-1/3}{v}_{0}t+1\right)}^{1/4}-1\right\}\end{array}}$

Cuando g≠0

Las ecuaciones que tenemos que resolver son

${\displaystyle \begin{array}{l}\frac{dm}{dt}=k{m}^{\alpha }v\\ m\frac{dv}{dt}+v\frac{dm}{dt}=mg\end{array}}$

Con la notación

${\displaystyle \dot{m}=\frac{dm}{dt}\dot{v}=\frac{dv}{dt}\dot{\dot{v}}=\frac{d\dot{v}}{dt}=\frac{d^{2}v}{d{t}^2}}$

Las ecuaciones anteriores se escriben

${\displaystyle \begin{array}{l}\dot{m}=k{m}^{\alpha }v\\ m\dot{v}+v\dot{m}=mg\end{array}}$

En general, la aceleración de la gota dv/dt no es constante, para que fuese constante se debería cumplir que

${\displaystyle \frac{\dot{m}}{m}v=g-c}$

donde c es una constante

Eliminado la derivada de m en las dos ecuaciones que describen el movimiento de la gota, obtenemos una ecuación diferencial de primer orden en v.

${\displaystyle \begin{array}{l}\dot{m}=k{m}^{\alpha }v\\ \dot{v}+k{m}^{\alpha -1}{v}^2=g{m}^{-\alpha +1}=k\frac{v^2}{g-\dot{v}}\end{array}}$

Derivamos respecto del tiempo

${\displaystyle \begin{array}{l}(-\alpha +1)m^{-\alpha }\dot{m}=k\frac{2v\dot{v}(g-\dot{v})-v^2(-\dot{\dot{v}})}{g-\dot{v}}(-\alpha +1)kv=k\frac{2v\dot{v}(g-\dot{v})-v^2(-\dot{\dot{v}})}{g-\dot{v}}\\ \dot{\dot{v}}=\frac{(g-\dot{v})}{v}\left((1-\alpha )g-(3-\alpha )\dot{v}\right)\end{array}}$

Esta ecuación diferencial no tiene solución analítica conocida

La aceleración es constante cuando el término entre paréntesis es cero

${\displaystyle \begin{array}{l}\dot{\dot{v}}=0\\ \dot{v}=\frac{1-\alpha }{3-\alpha }g\end{array}}$

Cuando α=2/3, la aceleración es constante e igual a 1/7 de la aceleración de la gravedad g

${\displaystyle \frac{dv}{dt}=\frac{1}{7}g}$

Procedimiento numérico

Se resuelve la ecuación diferencial de segundo orden por el procedimiento de Runge-Kutta

${\displaystyle \begin{array}{l}\frac{d^{2}x}{dt}=-k{m}^{\alpha -1}{v}^2+g\\ m^{1-\alpha }=(1-\alpha )kx+m_0^{1-\alpha }\end{array}}$

Con las condiciones iniciales t=0, v=0, m=m₀

La masa inicial m₀ en gramos es el producto de la densidad del agua 1.0 g/cm³ por el volumen de una esfera de radio r₀ en cm

${\displaystyle m_0=\frac{4}{3}\pi r_0^3}$

El valor de la constante de proporcionalidad k es

${\displaystyle k=\frac{{\rho }_n\pi }{{\left({\rho }_a\frac{4}{3}\pi \right)}^{2/3}}=\frac{{10}^{-6}\pi }{{\left(\frac{4}{3}\pi \right)}^{2/3}}=1.21·{10}^{-6}}$

Donde ρ_n≈10^-6 g/cm³ es la densidad de la niebla, y ρ_a=1.0 g/cm³ es la densidad del agua. La constante de proporcionalidad k es por tanto, del orden de 10^-6.

La aceleración de la gravedad es g=980 cm/s².

Actividades

Se introduce

• El radio inicial r₀ de la gota en mm, actuando en la barra de desplazamiento titulada Radio inicial

• La constante de proporcionalidad k en el intervalo 0.1·10^-6 a 9.0·10^-6, actuando en la barra de desplazamiento titulada Parámetro k.

Se pulsa el botón titulado Empieza

Se observa la caída de la gota de agua en la parte izquierda del applet

Se representa la aceleración dv/dt de la gota en función del tiempo t, observando que tiende hacia el valor límite g/7=1.4 m/s².

Vemos como la gota cambia su tamaño a medida que absorbe las pequeñas gotas suspendidas en el aire y que forman la niebla.

Referencias

Adawi I. Comments on the raindrop problem. Am. J. Phys. 54 (8) August 1986, pp. 739-740

Curso Interactivo de Física en Internet © Ángel Franco García