• Inicio
• Electromagnetismo
• Campo eléctrico

Campo eléctrico y potencial producido por un anillo uniformemente cargado

En esta página se calcula el campo eléctrico y el potencial producido por un anillo uniformemente cargado en un punto de su eje de simetría. Aplicaremos el resultado obtenido para calcular el campo y potencial producido por un disco de radio R, uniformemente cargado y finalmente, el campo producido por un plano indefinido, cuando el radio del disco se hace muy grande.

Sin embargo, el campo y el potencial en un punto fuera del eje del anillo requiere el cálculo de integrales elípticas completas de primera y segunda especie.

El anillo de radio a contiene una carga q uniformemente distribuida en su longitud.

Potencial producido por el anillo en un punto z de su eje de simetría

La carga dista r del punto P, luego el potencial es ${\displaystyle V=\frac{1}{4\pi {\epsilon }_0}\frac{q}{\sqrt{a^2+z^2}}}$

 

Campo eléctrico producido por el anillo en un punto de su eje de simetría

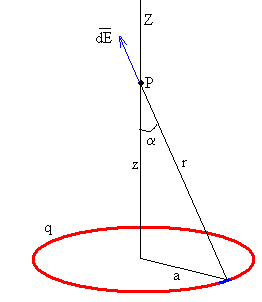El campo producido por el elemento de carga dq en el punto P vale ${\displaystyle \frac{1}{4\pi {\epsilon }_0}\frac{dq}{r^2}}$

Por simetría, las componentes de dicho campo perpendiculares al eje de simetría correspondientes a dos elementos de carga diametralmente opuestos se anulan de dos. El campo total es paralelo al eje Z de simetría y vale ${\displaystyle \begin{array}{l}E={\displaystyle \oint \frac{1}{4\pi {\epsilon }_0}\frac{dq}{r^2}\cos \alpha }=\frac{1}{4\pi {\epsilon }_0}\frac{q}{a^2+z^2}\frac{z}{\sqrt{a^2+z^2}}=\\ \frac{1}{4\pi {\epsilon }_0}\frac{qz}{{\left(a^2+z^2\right)}^{3/2}}\end{array}}$

El campo también se puede obtener a partir del potencial

${\displaystyle E=-\frac{dV}{dz}=\frac{1}{4\pi {\epsilon }_0}\frac{qz}{{(a^2+z^2)}^{3/2}}}$

Disco uniformemente cargado

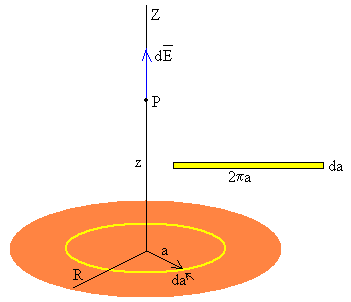Consideremos un disco de radio R, uniformemente cargado con una densidad de carga σ C/m2 El campo dE producido por un anillo de radio a y de anchura da, que contiene una carga dq=σ·2πa·da es ${\displaystyle dE=\frac{1}{4\pi {\epsilon }_0}\frac{z·dq}{{\left(a^2+z^2\right)}^{3/2}}=\frac{1}{4\pi {\epsilon }_0}\frac{z·\sigma ·2\pi a·da}{{\left(a^2+z^2\right)}^{3/2}}}$

El campo total producido por el disco cargado es la suma de los campos producidos por todos los anillos que forman el disco.

${\displaystyle E={\displaystyle \underset{0}{\overset{R}{\int }}\frac{1}{4\pi {\epsilon }_0}\frac{z·\sigma ·2\pi a·da}{{\left(a^2+z^2\right)}^{3/2}}=}\frac{\pi z·\sigma }{4\pi {\epsilon }_0}{\displaystyle \underset{0}{\overset{R}{\int }}\frac{2a·da}{{\left(a^2+z^2\right)}^{3/2}}}=\frac{z·\sigma }{2{\epsilon }_0}\left(\frac{1}{z}-\frac{1}{\sqrt{R^2+z^2}}\right)}$

Para un plano indefinido cargado R→∞

${\displaystyle E=\frac{\sigma }{2{\epsilon }_0}}$

El mismo resultado se obtiene aplicando la ley de Gauss.

Potencial producido por el anillo cargado en un punto fuera del eje

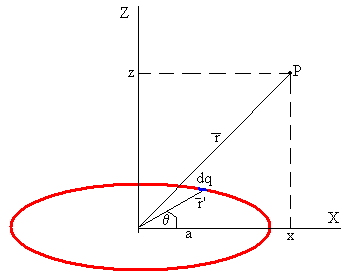Calculamos el potencial en el punto P del plano XZ producido por un elemento diferencial de carga dq=λ·dl, donde λ=q/(2πa) es la densidad lineal de carga en C/m, dl=a·dθ es la longitud de un arco diferencial, El vector r’= a·cosθi+ a·senθj señala la posición del elemento diferencial de carga El vector r=xi+zk señala la posición del punto P

El potencial en el punto  P vale

${\displaystyle V=\frac{1}{4\pi {\epsilon }_0}{\displaystyle \oint \frac{\lambda ·dl}{\left|r-r\text{'}\right|}}}$

donde |r-r’| es la distancia entre el elemento diferencial de carga dq y el punto P.

${\displaystyle \left|r-r\text{'}\right|=\sqrt{{(x-a\cos \theta )}^2+a^2{\sin }^2\theta +z^2}=\sqrt{x^2+a^2+z^2-2ax\cos \theta }}$

La integral se convierte en

${\displaystyle \begin{array}{l}{\displaystyle \oint \frac{\lambda ·a·d\theta }{\sqrt{x^2+z^2+a^2-2ax\cos \theta }}}=\frac{2}{4\pi {\epsilon }_0}{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{\lambda ·a·d\theta }{\sqrt{x^2+z^2+a^2-2ax\cos \theta }}}=\\ \frac{\lambda a}{2\pi {\epsilon }_0\sqrt{2ax}}{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{d\theta }{\sqrt{b-\cos \theta }}}b=\frac{z^2+x^2+a^2}{2ax}\end{array}}$

Las tablas de integrales elípticas (Good) nos da la siguiente equivalencia

${\displaystyle {\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{d\theta }{\sqrt{b-\cos \theta }}}=\sqrt{2m}K(m)K(m)={\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{d\phi }{\sqrt{1-m{\sin }^2\phi }}}m=\frac{2}{1+b}}$

K(m) es la integral elíptica completa de primera especie

El potencial V en el punto P vale

${\displaystyle V=\frac{\lambda }{2\pi {\epsilon }_0}\sqrt{\frac{a}{2x}}\sqrt{2m}K(m)m=\frac{2}{1+\frac{z^2+x^2+a^2}{2ax}}}$

El valor de K(m) se puede consultar en una tabla de integrales elípticas (Puig Adam)

Campo eléctrico producido por el anillo cargado en el punto fuera del eje

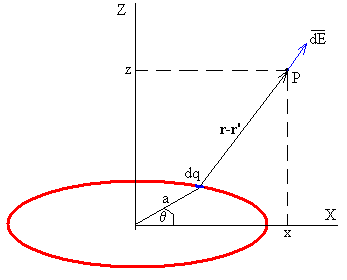Calculamos el campo eléctrico en el punto P del plano XZ producido por un elemento diferencial de carga dq=λ·dl, donde λ=q/(2πa) es la densidad lineal de carga en C/m, dl=a·dθ es la longitud de un arco diferencial, El vector r’= a·cosθi+ a·senθj señala la posición del elemento diferencial de carga El vector r=xi+zk señala la posición del punto P

El campo eléctrico producido por el elemento diferencial de carga dE tiene la dirección y el sentido del vector diferencia r-r’, que une la posición de la carga y el punto P.

${\displaystyle dE=\frac{1}{4\pi {\epsilon }_0}\frac{\lambda ·dl}{{\left|r-r\text{'}\right|}^2}\frac{r-r\text{'}}{\left|r-r\text{'}\right|}=\frac{1}{4\pi {\epsilon }_0}\frac{\lambda ·dl}{{\left|r-r\text{'}\right|}^3}(r-r\text{'})}$

Las componentes del campo total son:

${\displaystyle \begin{array}{l}{E}_x=\frac{\lambda a}{4\pi {\epsilon }_0}{\displaystyle \oint \frac{x-a\cos \theta }{{(x^2+z^2+a^2-2ax\cos \theta )}^{3/2}}}d\theta \\ E_y=\frac{\lambda a}{4\pi {\epsilon }_0}{\displaystyle \oint \frac{-a\sin \theta }{{(x^2+z^2+a^2-2ax\cos \theta )}^{3/2}}}d\theta \\ E_z=\frac{\lambda a}{4\pi {\epsilon }_0}{\displaystyle \oint \frac{z}{{(x^2+z^2+a^2-2ax\cos \theta )}^{3/2}}}d\theta \end{array}}$

Por simetría, la componente Y del campo debe anularse, como puede comprobarse fácilmente resolviendo la integral inmediata.

Como cosθ es una función par podemos hace la sustitución ${\displaystyle \underset{0}{\overset{2\pi }{\int }}}\to 2{\displaystyle \underset{0}{\overset{\pi }{\int }}}$

El resultado es

${\displaystyle \begin{array}{l}{E}_x=\frac{2\lambda a}{4\pi {\epsilon }_0}{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{x-a\cos \theta }{{\left(x^2+z^2+a^2-2ax\cos \theta \right)}^{3/2}}d\theta }=\frac{\lambda a}{2\pi {\epsilon }_0}\frac{1}{{\left(2ax\right)}^{3/2}}\left(x{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{d\theta }{{\left(b-\cos \theta \right)}^{3/2}}}-a{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{\cos \theta ·d\theta }{{\left(b-\cos \theta \right)}^{3/2}}}\right)\\ E_z=\frac{2\lambda a}{4\pi {\epsilon }_0}{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{z}{{\left(x^2+z^2+a^2-2ax\cos \theta \right)}^{3/2}}}d\theta =\frac{\lambda a}{2\pi {\epsilon }_0}\frac{1}{{\left(2ax\right)}^{3/2}}z{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{d\theta }{{\left(b-\cos \theta \right)}^{3/2}}}\end{array}}$  

Las tablas de integrales elípticas (Good) nos da las siguientes equivalencias

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{d\theta }{{\left(b-\cos \theta \right)}^{3/2}}}=\frac{m}{2-2m}\sqrt{2m}E\left(\sqrt{m}\right)E\left(\sqrt{m}\right)={\displaystyle \underset{0}{\overset{\pi /2}{\int }}\sqrt{1-m{\sin }^2\phi }d\phi }m=\frac{2}{1+b}\\ {\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{-\cos \theta ·d\theta }{{\left(b-\cos \theta \right)}^{3/2}}}=\sqrt{2m}K\left(\sqrt{m}\right)-\frac{2-m}{2-2m}\sqrt{2m}E\left(\sqrt{m}\right)K\left(\sqrt{m}\right)={\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{d\phi }{\sqrt{1-m{\sin }^2\phi }}}\end{array}}$

Las expresiones de las componentes del campo son, ahora,

${\displaystyle \begin{array}{l}{E}_x=\frac{q}{4{\pi }^2{\epsilon }_0}\frac{1}{{\left(2ax\right)}^{3/2}}\left(x\frac{m}{2-2m}\sqrt{2m}E\left(\sqrt{m}\right)+a\sqrt{2m}K\left(\sqrt{m}\right)-a\frac{2-m}{2-2m}\sqrt{2m}E\left(\sqrt{m}\right)\right)\\ E_z=\frac{q}{4{\pi }^2{\epsilon }_0}\frac{1}{{\left(2ax\right)}^{3/2}}z\frac{m}{2-2m}\sqrt{2m}E\left(\sqrt{m}\right)m=\frac{4ax}{x^2+z^2+a^2+2ax}\end{array}}$

En la figura, se muestra la dirección del campo eléctrico mediante flechas, en el plano XZ, con x>0  y z>0. El módulo del campo no se puede mostrar ya que cambia significativamente de un punto cercano al anillo a otro algo más alejado. El radio del anillo es a=1.0

Caso particular

Estudiamos el campo a lo largo del eje del anillo, x →0,

${\displaystyle m\to \frac{4ax}{z^2+a^2}}$

Las integrales elípticas tienden ambas a K(0)=E(0)=π/2

Como podemos comprobar fácilmente E_x→0, fijarse que los dos últimos términos entre paréntesis se cancelan y E_x en el límite, resulta proporcional a x. En cuanto a la componente Z.

${\displaystyle E_z\to \frac{q}{4{\pi }^2{\epsilon }_0}\frac{1}{{(2ax)}^{3/2}}z\frac{\frac{4ax}{z^2+a^2}}{2}\sqrt{2\frac{4ax}{z^2+a^2}}\frac{\pi }{\text{2}}=\frac{1}{4\pi {\epsilon }_0}\frac{qz}{{\left(a^2+z^2\right)}^{3/2}}}$

Resultado que hemos obtenido previamente.

Actividades

Se introduce

• La abscisa (x/a) del punto P, actuando en la barra de desplazamiento titulada Abscisa

• La ordenada (z/a) del punto P, actuando en la barra de desplazamiento titulada Ordenada

Se pulsa en el botón titulado Calcular

El programa interactivo calcula las componentes E_x y E_z del campo, su módulo y el ángulo que forma con el eje X.

Las componentes del campo E_x y E_z se expresan en términos de (x/a) y (z/a) y de las integrales elípticas completas de la siguiente forma

${\displaystyle \begin{array}{l}{E}_x=\frac{q}{4\pi a^2{\epsilon }_0}\frac{1}{\pi {\left(2(x/a)\right)}^{3/2}}\left(\left(\frac{x}{a}\right)\frac{m}{2-2m}\sqrt{2m}E\left(\sqrt{m}\right)+\sqrt{2m}K\left(\sqrt{m}\right)-\frac{2-m}{2-2m}\sqrt{2m}E\left(\sqrt{m}\right)\right)\\ E_z=\frac{q}{4\pi a^2{\epsilon }_0}\frac{1}{\pi {\left(2(x/a)\right)}^{3/2}}\left(\frac{z}{a}\right)\frac{m}{2-2m}\sqrt{2m}E\left(\sqrt{m}\right)m=\frac{4(x/a)}{{\left(x/a\right)}^2+{\left(z/a\right)}^2+1+2(x/a)}\end{array}}$

El campo en un punto del eje Z se expresa en términos de (z/a)

${\displaystyle E_z=\frac{q}{4\pi a^2{\epsilon }_0}\frac{(z/a)}{{\left(1+{\left(z/a\right)}^2\right)}^{3/2}}}$

El programa interactivo calcula el valor de E_x y de E_y proporcionales a la constante$\frac{q}{4\pi a^2{\epsilon }_0}$

ForzadasApplet aparecerá en un explorador compatible con JDK 1.1.

Referencias

Good R. H. Elliptic integrals, the forgotten functions. Eur. J. Phys. 22 (2001) pp. 119-126.

Zypman F. R., Electric field of a ring of charge. Am. J. Phys. 74 (4) April 2006, pp. 295-300.

Puig Adam P. Curso teórico de cálculo integral aplicado a la Física y a la Técnica. Biblioteca Matemática, 1972, págs.71-73.

Curso Interactivo de Física en Internet © Ángel Franco García