• Inicio
• Electromagnetismo
• Campo magnético

Campo magnético producido por una corriente rectilínea indefinida de sección circular.

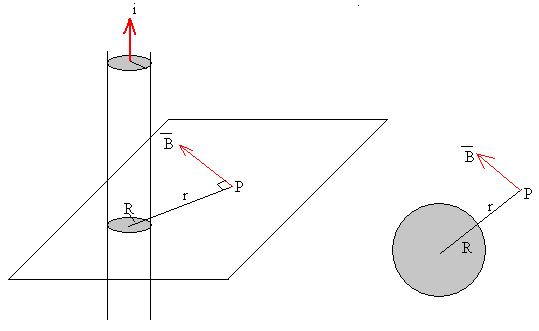
Apliquemos la ley de Ampère a una corriente rectilínea indefinida uniformemente distribuida en su sección y que circula a lo largo de un cilindro radio interior a.

1. La dirección del campo magnético en el punto P es perpendicular al plano determinado por el eje de la corriente cilíndrica y el punto P, es decir, tangente a la circunferencia de radio r con centro en el eje y que pasa por el punto P.
    
2. La simetría de la distribución de corrientes nos indica que el camino cerrado que tenemos que elegir es una circunferencia de radio r, centrada en el eje del cilindro y situada en una plano perpendicular al mismo. La circulación del campo magnético B a lo largo de dicha circunferencia tiene la misma expresión que para la corriente rectilínea

B·2π r

3. Vamos a calcular ahora la intensidad que atraviesa la circunferencia de radio r (en color azul) en los dos casos siguientes.

• r<a

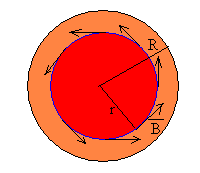4.-Como vemos en la figura, la intensidad que atraviesa la circunferencia de radio r<R es una parte de la intensidad total i. ${\displaystyle i\frac{\pi r^2}{\pi R^2}}$

5.-Aplicando la ley de Ampère

${\displaystyle B·2\pi r={\mu }_{0}i\frac{r^2}{R^2}B=\frac{{\mu }_{0}i}{2\pi R^2}r}$

• r>a

4.-La intensidad que atraviesa la circunferencia de radio r>R es i

5.-Aplicando la ley de Ampère

${\displaystyle B·2\pi r={\mu }_{0}iB=\frac{{\mu }_{0}i}{2\pi r}}$

Campo magnético producido por una corriente que circula a lo largo de un cilindro hueco.

En el siguiente applet se representa mediante flechas el campo magnético producido por una corriente rectilínea indefinida, perpendicular al plano del applet y dirigida hacia el lector.

Pulsando en el botón titulado Siguiente, se representa el campo magnético producido por dos, tres, cuatro, etc, corrientes rectilíneas indefinidas situadas sobre la superficie lateral y paralelas al eje de un cilindro de radio a.

Cuando el número de corrientes equidistantes es grande, se anula el campo magnético en el interior, (para r<a), en el exterior el campo magnético es tangente a circunferencias concéntricas de radio r>a. Vamos a ver cómo en esta situación es aplicable la ley de Ampère.

SolenoideApplet aparecerá en un explorador compatible JDK 1.1

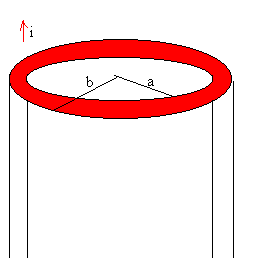Apliquemos la ley de Ampère a una corriente rectilínea indefinida uniformemente distribuida en su sección y que circula a lo largo de un cilindro hueco de radio interior a y exterior b.

1. Como hemos observado en el applet, la dirección del campo magnético en el punto P es perpendicular al plano determinado por el eje de la corriente cilíndrica y el punto P, es decir, tangente a la circunferencia de radio r con centro en el eje y que pasa por el punto P.
    
2. La simetría de la distribución de corrientes nos indica que el camino cerrado que tenemos que elegir es una circunferencia de radio r, centrada en el eje del cilindro y situada en una plano perpendicular al mismo. La circulación del campo magnético B a lo largo de dicha circunferencia tiene la misma expresión que para la corriente rectilínea

B·2π r

3. Vamos a calcular ahora la intensidad que atraviesa la circunferencia de radio r (en color azul) en los tres casos siguientes.

• r<a

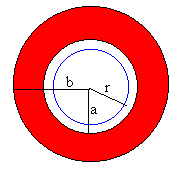Como vemos en la figura, la intensidad que atraviesa la circunferencia de radio r<a es cero. Aplicando la ley de Ampère B·2π r=μ 0 ·0 B=0 El campo magnético es nulo para r<a tal como hemos comprobado en el applet.

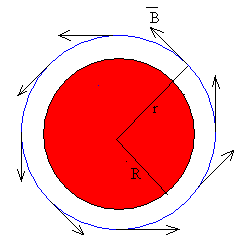
• a<r<b

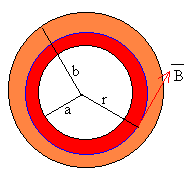Como vemos en la figura, la intensidad que atraviesa la circunferencia de radio a<r<b es una parte de la intensidad total i. Si la corriente i está uniformemente distribuida en la sección π b2-π a2. La corriente que atraviesa la circunferencia de radio r es la que pasa por la sección pintada de color rojo, cuya área es π r2-πa2.

${\displaystyle i\frac{\pi r^2-\pi a^2}{\pi b^2-\pi a^2}}$

Aplicando la ley de Ampère

${\displaystyle B·2\pi r={\mu }_{0}i\frac{\pi r^2-\pi a^2}{\pi b^2-\pi a^2}B=\frac{{\mu }_{0}i}{2\pi r}\frac{r^2-a^2}{b^2-a^2}}$

• r>b

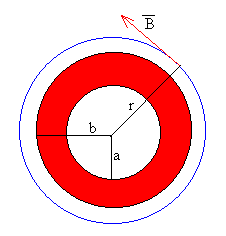Como vemos en la figura, la intensidad que atraviesa la circunferencia de radio r>b es la intensidad i. El módulo del campo magnético B en un punto P situado a una distancia r del eje de la corriente cilíndrica es ${\displaystyle B·2\pi r={\mu }_{0}iB=\frac{{\mu }_{0}i}{2\pi r}}$

Curso Interactivo de Física en Internet © Ángel Franco García