Materiales paramagnéticos

Método de Montecarlo. Variable aleatoria discreta

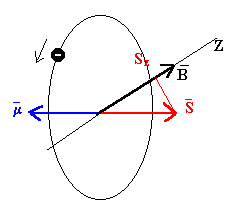Un átomo o un ión de momento magnético μ en un campo magnético B tiene una energía U=-µ·B. El momento magnético es proporcional al momento angular µ=gµ_BS. Donde μ_B=9.2732·10^-24 J/T es el magnetón de Bohr y g es un factor del orden de dos.

Si B apunta en la dirección del eje Z, la energía del dipolo vale U=-µ·B=--μ_zB=-gµ_BmB

En la descripción mecánico-cuántica la componente Z del momento angular pude tomar solamente 2S+1 valores que van desde m=-S a m=+S. Utilizando la descripción clásica esta restricción nos viene a decir que no todas las orientaciones del momento magnético son posibles, sino aquellas tales que su componente a lo largo de la dirección del campo tiene el valor indicado. Por ejemplo, si el ion Cr(3+) tiene un momento angular S=3/2, su momento magnético en unidades del magnetón de Bohr es μ=gS=3. Las posibles orientaciones son -3/2, -1/2, 1/2 y 3/2, es decir 4.

Aplicaremos la fórmula de la estadística clásica a 2S+1 niveles discretos. Así, la probabilidad de que un ion tenga una energía E_m o bien, que la componente Z de su momento magnético (en unidades del magnetón de Bohr) valga gm es

$P (m) = C \cdot \exp (\frac{- E_{m}}{k T})$

La constante de proporcionalidad se determina teniendo en cuenta todos los posibles estados de los componentes del sistema magnético. Luego,

$P (m) = \frac{\exp (\frac{g μ_{B} m B}{k T})}{\sum_{m = - S}^{S} \exp (\frac{g μ_{B} m B}{k T})}$

La componente del momento magnético medio en la dirección del campo magnético vale:

$< μ_{z} > = \frac{\sum_{m = - S}^{S} μ_{z} \exp (g μ_{B} m B / k T)}{\sum_{m = - S}^{S} \exp (g μ_{B} m B / k T)} = \sum_{m = - S}^{S} g μ_{B} m P (m) = g μ_{B} B (u) u = \frac{g μ_{B} B}{k T}$

La función B(u) se denomina función de Brillouin y es equivalente a la función de Langevin para los dipolos eléctricos

Podemos considerar dos situaciones extremas:

Cuando u<<<1 la componente del momento magnético medio se puede aproximar a la expresión:

$< μ_{z} > = \frac{g^{2} μ_{B}^{2} S (S + 1)}{3 k} \frac{B}{T}$

El momento magnético medio <μ_z> y por tanto, la imanación M=N<μ_z> es una función lineal del cociente campo/temperatura, a esta fórmula se le conoce como ley de Curie.

Cuando u es grande, es decir, cuando el campo magnético es intenso o la temperatura es baja, la mayor parte de los momentos magnéticos están orientados según el campo

<μ_z>=gμ_BS

En la aplicación del método de Montecarlo hemos de transformar la variable aleatoria con distribución de probabilidad dada P(m), a partir de los valores de una variable aleatoria uniformemente distribuida en el intervalo [0, 1), según se esquematiza en el apartado variable aleatoria discreta. Se obtendrá el resultado m, es decir, una partícula del sistema estará en el nivel de energía E_m, si al sortear un número aleatorio γ uniformemente distribuido en el intervalo [0, 1), se cumple la condición (1)

La clase que describe el sistema físico

Los miembros dato de la clase Paramagnetico son el momento magnético mu del material en unidades del magnetón de Bohr, un número impar (1, 3, 5 o 7) dependiendo del tipo de ion paramagnético, un array p donde se guardan las probabilidades acumuladas para efectuar el sorteo de la variable aleatoria discreta, y el número de partículas del sistema nParticulas. La constante COEFICIENTE guarda el cociente ente el magnetón de Bohr y la constante de Boltzmann.

El constructor recibe como datos, el número de partículas del sistema y el momento magnético en unidades del magnetón de Bohr, y crea el array p que guarda las probabilidades. Por ejemplo, si el momento magnético es 3 tendrá que crear un array de 4 elementos ya que hay 2·3/2+1 posibles orientaciones del momento angular, y por tanto, cuatro posibles estados o niveles donde pueden situarse los iones

public class Paramagnetico {
    private int mu;         	//momento magnético en unidades de Bohr
    private double[] p;  	//distribución de probabilidades de ocupación
    public int nParticulas;
//números aleatorios
    private Random rnd=new Random();
    private static final double COEFICIENTE=9.2732e-24/1.3805e-23;  
   //Magnetón de Bohr/cte de Boltzmann

    public Paramagnetico(int nParticulas, int momento) {
        this.nParticulas=nParticulas;
        mu=momento;
        p=new double[mu+1];
    }
//funciones miembro ...
}

La función miembro probabilidades, calcula las probabilidades p_i, de acuerdo con las fórmulas descritas en la la clase Niveles de la página anterior, y las probabilidades acumuladas, guandándolas en cada uno de los elementos del array p.

    private void probabilidades(double campo, double temperatura){
        for(int i=0; i<=mu; i++){
            p[i]=Math.exp(COEFICIENTE*(2*i-mu)*campo/temperatura);
        }
//acumulada
        for(int i=1; i<=mu; i++){
            p[i]+=p[i-1];
        }
//normalizar
        for(int i=0; i<=mu; i++){
            p[i]/=p[mu];
        }
    }

La función miembro sorteo determina el estado de cada uno de los iones, de acuerdo con el procedimiento descrito en el apartado variable aleatoria discreta, o en la página anterior (función miembro distribucion), devolviendo el momento magnético de un ion particular.

    private int sorteo(){
        int i=0;
        for(i=0; i<=mu; i++){
            if(Math.random()<p[i]){
                break;
            }
        }
        return (2*i-mu);    //momento magnético
    }

Por último, hemos de determinar el estado de una muestra significativa de iones para calcular el momento magnético medio en función del campo magnético y de la temperatura. Obtenemos el momento magnético de cada ión mediante la función miembro sorteo, por último dividimos el momento magnético total entre el número de iones de la muestra. La función miembro momentoMagneticoMedio nos devuelve el momento magnético medio de la muestra paramagnética en unidades del magnetón de Bohr. Como caso particular, consideramos aquél en el que la temperatura es cero, todos los momentos magnéticos apuntan en la dirección del campo.

    public double momentoMagneticoMedio(double campo, double temperatura){
        if(temperatura<=0.0){
            return mu;
        }
        probabilidades(campo, temperatura);
        int media=0;
        for(int i=0; i<nParticulas; i++){
            media+=sorteo();
        }
        return (double)media/nParticulas;
    }

Creamos un objeto param de la clase Paramagnetico y le pasamos al constructor el número de iones 1000 y el momento magnético de la muestra por ejemplo, el Cr (3+) que tiene un momento magnético de 3 unidades. Fijamos la intensidad del campo magnético en 2 Tesla, y analizamos el comportamiento de la muestra para diversas temperaturas.

        Paramagnetico param=new Paramagnetico(1000, 3);
        double campo=2.0; 		//Teslas
        System.out.println("temperatura \t m. magnético medio");
        for(double T=0.0; T<20; T+=1.0){
            System.out.println(" "+T+ " \t \t"+
             (double)Math.round(100*param.momentoMagneticoMedio(campo, T))/100);
        }

Ejercicio

En la siguiente tabla se proporcionan los momentos magnéticos en unidades de Bohr de varios iones paramagnéticos

Ion	Momento magnético ( u. Bohr)
Gd (3+)	7
Fe (3+)	5
Cr (3+)	3
Co (3+)	1

Completar tablas en las que fijada la intensidad del campo magnético y el tipo de material, se obtenga el momento magnético medio en función de la temperatura.

Comprobar la ley de Curie