Fluido viscoso entre dos cilindros coaxiales

En esta página, vamos a determinar la distribución de las velocidades angulares del fluido entre dos cilindros coaxiales en rotación y a calcular el momento que ejerce el fluido viscoso respecto del eje de rotación.

Emplearemos la expresión deducida para diseñar una experiencia que nos permita medir la viscosidad del fluido

Momento que ejerce el fluido

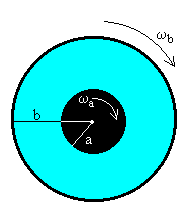Consideremos el movimiento de un fluido entre dos cilindros coaxiales tal como se indica en la figura. Sea a el radio del cilindro interior y b el del cilindro exterior. Sean ω_a la velocidad angular de rotación del cilindro interior y ω_b la velocidad angular del exterior.

En la página anterior, al estudiar el concepto de viscosidad, vimos que la fuerza por unidad de área era proporcional al gradiente de velocidad, la constante de proporcionalidad se denomina viscosidad η

$\frac{F}{A} = η \frac{d v}{d x}$

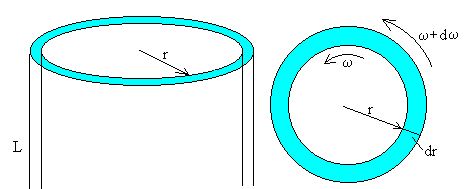
En este caso, la capa de fluido considerada es de forma cilíndrica de espesor dr. La velocidad angular ω varía con la distancia radial r. El gradiente de velocidad se expresa en coordenadas cilíndricas

$\frac{F}{A} = η r \frac{d ω}{d r}$

El área A de una superficie lateral de un cilindro de radio r y altura L es 2π rL.

Teniendo en cuenta que, la magnitud relevante en la dinámica de rotación es el momento no la fuerza. El momento M de la fuerza F respecto del eje de rotación es M=Fr.

$M = 2 π r^{3} L η \frac{d ω}{d r}$

Como el movimiento de fluido es estacionario, M debe de ser independiente de r, esto significa que

$\begin{array}{l} r^{3} \frac{d ω}{d r} = c_{1} \\ M = 2 π L η c_{1} \end{array}$

donde c₁ es una constante a determinar. Integrando

$ω = - \frac{c_{1}}{2 r^{2}} + c_{2}$

Las constantes c₁ y c₂ se determinan sabiendo que las velocidades del fluido en las superficies interior y exterior de los cilindros coaxiales son respectivamente

Para r=a, ω =ω_a
Para r=b, ω =ω_b.

$c_{1} = \frac{2 a^{2} b^{2}}{b^{2} - a^{2}} (ω_{a} - ω_{b}) c_{2} = \frac{b^{2} ω_{b} - a^{2} ω_{a}}{b^{2} - a^{2}}$

y el momento respecto del eje de rotación es

$M = \frac{4 π η L a^{2} b^{2}}{b^{2} - a^{2}} (ω_{b} - ω_{a})$

proporcional a la velocidad angular relativa de los cilindros.

Actividades

El programa interactivo trata de mostrar visualmente la distribución de las velocidades angulares del fluido entre los dos cilindros coaxiales, cuando se introduce las velocidades angulares ω_a y ω_b, y el radio del cilindro interior a. El radio del cilindro exterior se ha fijado en el programa, de modo que b=1.0.

Se introduce

la velocidad angular del cilindro interior, seleccionado 0, 1, 2 ó 3 en el control de selección titulado V. angular (interior)
la velocidad angular del cilindro exterior, seleccionado 0, 1, 2, 3, -1, -2, -3 en el control de selección titulado V. angular (exterior).
el radio del cilindro interior a, en el control de selección titulado Radio interior.
el radio del cilindro exterior se ha fijado en b=1.0,

Se pulsa el botón titulado Empieza

A la izquierda del applet, se muestra el movimiento de las partículas de fluido situados a distancias variables del eje de los cilindros. A la derecha, se muestra una gráfica del perfil de la velocidad angular de dichas partículas en función de su distancia radial al eje de los dos cilindros coaxiales.

FluidoApplet1 aparecerá en un explorador compatible con JDK 1.1.

Medida de la viscosidad de un fluido

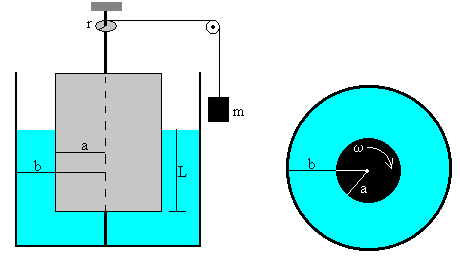
En este apartado, se describe una experiencia para la medida de la viscosidad de un fluido, utilizando un cilindro interior que gira en un recipiente cilíndrico de mayor radio que contiene el fluido. En la figura se muestra el dispositivo experimental

El cilindro móvil de radio a que gira con velocidad angular ω.
El fluido de viscosidad η desconocida.
El recipiente de radio b, que se llena de fluido hasta que la base del cilindro esté a una profundidad L.
El eje de rotación tiene una polea de radio r, en la que se enrolla una cuerda, que se une a un bloque de masa m que cuelga de su extremo.

El momento respecto del eje de rotación que ejerce el fluido viscoso cuando el cilindro interior gira con velocidad angular ω_a=ω, y el exterior está en reposo ω_b=0 es

$M = \frac{4 π a^{2} b^{2}}{b^{2} - a^{2}} η L ω$

Este momento frena el movimiento de rotación el cilindro

Cuando le aplicamos un momento exterior mgr al cilindro, inicialmente en reposo, se pone en movimiento, alcanzando rápidamente una velocidad angular constante límite ω tal que

$m g r = \frac{4 π a^{2} b^{2}}{b^{2} - a^{2}} η L ω$

Recuérdese que en los experimentos de medida de la viscosidad por el método de Stokes. Una bolita que cae en el seno de un fluido, cuya viscosidad es elevada (por ejemplo, aceite de automóvil) alcanza una velocidad límite constante prácticamente desde el momento en que se libera.

Del mismo modo, cuando se suelta el bloque, el cilindro adquiere muy pronto una velocidad angular de rotación constante.

En la experiencia real, además del rozamiento en los ejes del cilindro y de las poleas, típicos de cualquier experiencia en mecánica, tenemos un rozamiento en la base del cilindro que será una función de la velocidad angular de rotación ω. Estos factores no los tendremos en cuenta en la experiencia simulada.

Procedimiento de medida

Fijada la altura del líquido en el recipiente, se va cambiando la masa m del bloque que cuelga y se mide la velocidad angular de rotación ω del cilindro. Se representa la velocidad angular de rotación ω en el eje vertical y la masa m en el eje horizontal.

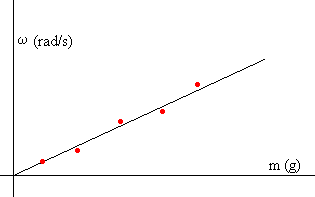
Se traza la recta

ω=K·m

Se calcula la pendiente K, en la experiencia real, aplicando el procedimiento de regresión lineal.

$ω = (\frac{b^{2} - a^{2}}{4 π a^{2} b^{2}} \frac{g r}{L η}) m$

Modificamos la altura del líquido en el recipiente, y volvemos a repetir las medidas.

Actividades

El programa interactivo genera un número aleatorio entre 0.35 y 0.60 que representa la viscosidad η del fluido.

Se introduce

La parte L, en cm, del cilindro que está sumergida en el fluido, actuando en la barra de desplazamiento titulada Longitud.
La masa m del bloque, en gramos, actuando en la barra de desplazamiento titulada Masa bloque.
El radio del cilindro se ha fijado en a=10 cm
El radio del recipiente b=15 cm
El radio de la polea r=2 cm

Se pulsa el botón titulado Empieza

Se cambia la masa m del bloque, manteniendo la longitud L constante. La regla situada a la derecha del applet, nos permite medir la velocidad constante v=x/t del bloque, la velocidad angular de rotación ω=v/r, donde r es el radio de la polea.

En la parte izquierda del applet, se recogen los pares de datos, masa del bloque m en gramos, velocidad angular de rotación ω en rad/s. Cuando se ha recogido varios pares de datos se pulsa en botón titulado Gráfica.

Se representan los pares de datos y la recta

ω=K·m

En la parte superior del applet, se nos proporciona el valor de la pendiente K a partir de este dato, calculamos la viscosidad η.

Como K viene expresado en rad/(g·s), se convierte en rad/(s·kg) multiplicando por 1000.

Despejamos la viscosidad de la fórmula

$K = \frac{b^{2} - a^{2}}{4 π a^{2} b^{2}} \frac{g r}{L η} K = \frac{{0.15}^{2} - {0.1}^{2}}{4 π {0.1}^{2} {0.15}^{2}} \frac{9.8 \cdot 0.02}{L η}$

Se cambia la longitud L de la parte del cilindro sumergida en el fluido y se vuelven a repetir las medidas.

FluidoApplet1 aparecerá en un explorador compatible con JDK 1.1.

Referencias

Hibberd F. H., A simple arrangement for a rotating cylinder viscosimeter. Am. J. Phys. 20 (1952) , pp. 134-135