Ecuación fundamental de la estática de fluidos
Variación de la presión con la profundidad
Consideremos una porción de fluido en equilibrio de altura dy y de sección S, situada a una distancia y del fondo del recipiente que se toma como origen.
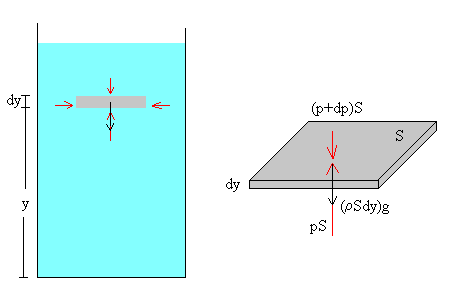
Las fuerzas que mantienen en equilibrio a dicha porción de fluido son las siguientes:
- El peso, que es igual al producto de la densidad del fluido, por su volumen y por la intensidad de la gravedad, (ρ S·dy)g.
- La fuerza que ejerce el fluido sobre su cara inferior, pS
- La fuerza que ejerce el fluido sobre su cara superior, (p+dp)S
La condición de equilibrio establece que
(ρ S·dy)g+pS=(p+dp)S
dp=-ρ·g·dy
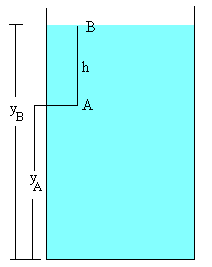 |
Integrando esta ecuación entre los límites que se indican en la figura
Situamos el punto B está en la superficie y el punto A a una profundidad h. Si p0 es la presión en la superficie del fluido (la presión atmosférica), la presión p a la profundidad h es p=p0+ρ gh |
Medida de la presión. Manómetro
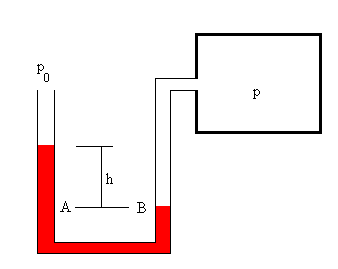 |
Para medir la presión empleamos un dispositivo denominado manómetro.
Como A y B están a la misma altura la presión en A y en B debe ser la misma. Por una
rama la presión en B es debida al gas encerrado en el recipiente. Por la otra rama la
presión en A es debida a la presión atmosférica más la presión debida a la diferencia
de alturas del líquido manométrico.
p=p0+ρ gh |
Experiencia de Torricelli
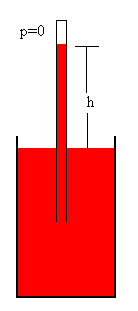 |
Para medir la presión atmosférica, Torricelli empleó un tubo largo,
cerrado por uno de sus extremos, lo llenó de mercurio y le dio la vuelta sobre una vasija
de mercurio. El mercurio descendió hasta una altura h=0.76 m al nivel del mar.
Dado que el extremo cerrado del tubo se encuentra casi al vacío p=0, y sabiendo la
densidad del mercurio es 13.55 g/cm3 ó 13550 kg/m3 el valor de la presión atmosférica es
|
Actividades
Con este applet se puede comprobar la ecuación fundamental de la estática de fluidos, es decir, que la presión varía linealmente con la altura. Al mismo tiempo, podemos ver como funciona un manómetro.
Se conecta un tubo por un extremo a un manómetro y por el otro a un elemento o cápsula de presión consistente en un cilindro de metal con un diafragma de goma, dispuesto para medir la presión hidrostática. El elemento de presión se introduce en el fluido a una profundidad h. En la práctica real, el elemento de presión se puede girar a fin de demostrar que la presión solamente depende de la posición, pero es independiente de la dirección en la que se mide.
En el programa interactivo podemos seleccionar uno de los fluidos cuyas densidades se recogen en la tabla y a continuación se pulsa en el botón titulado Nuevo.
| Sustancia | Densidad (kg/m3) |
| Agua | 1000 |
| Aceite | 900 |
| Alcohol | 790 |
| Glicerina | 1260 |
| Mercurio | 13550 |
La última sustancia es el líquido manométrico, el mercurio.
Arrastramos con el puntero del ratón el elemento de presión, señalado por una flecha de color rojo hasta la profundidad deseada. Podemos leer en el manómetro la presión, o también en la gráfica de la derecha, donde se representa la profundidad en el eje vertical y la presión en el eje horizontal.
Ejemplo:
Supongamos que el fluido es agua. Bajemos la cápsula de presión arrastrando con el puntero del ratón la flecha roja hasta una profundidad de 60 cm. La presión debida a la altura de fluido es
p=1000·9.8·0.6=5880 Pa
El manómetro marca 2.2 cm por ambas ramas, que corresponde a una presión de
p=13550·9.8·2·0.022=5843
Como el manómetro está abierto por el otro extremo, no nos mide la presión total (atmosférica más la altura de fluido) sino solamente la presión debida al fluido.
Como vemos en la gráfica de la derecha a la profundidad de 60 cm le corresponden algo menos de 106 000 Pa, que corresponden a la presión atmosférica (aproximadamente 100 000 Pa) más la presión debida a la altura de la columna de fluido (6000 Pa).
La gráfica de la derecha está trazada de forman no usual, ya que la presión (variable dependiente) debería estar en el eje vertical y la altura (variable independiente) en el eje horizontal. La gráfica por tanto, nos muestra la dependencia lineal de la presión p con la profundidad h.
p=p0+ρ gh
Se arrastra la flecha de color rojo con el puntero del ratón ![]()
