• Inicio
• Fluidos
• Tensión superficial

La forma que adopta una cuerda bajo la acción de su peso y de la tensión superficial.

Hemos estudiado en otra página, la forma que adopta una cadena que cuelga de sus extremos (la catenaria). En esta página, vamos a estudiar la forma que adopta una cuerda cuando el área encerrada por ésta y la varilla de que la sostiene se cubre con una película jabonosa.

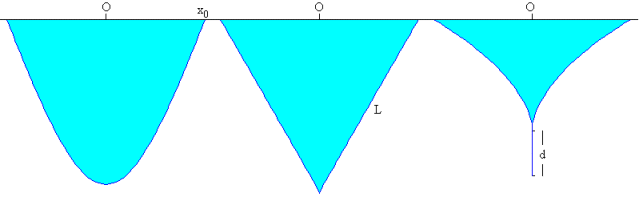
Veremos que el cociente entre la tensión superficial 2σ y la componente normal del peso de la cuerda por unidad de longitud λg determinan la forma de la cuerda. Cuando la tensión superficial domina, la cuerda adopta una forma convexa similar a la letra griega γ. Cuando la componente del peso domina, su forma es la de una catenaria distorsionada. Cuando ambas son iguales la cuerda adopta la forma lineal de una V.

Este ejemplo es particularmente relevante, ya que permite al lector practicar con el cálculo integral, los procedimientos numéricos y la representación gráfica de funciones. Para el programador, es un ejemplo interesante de aplicación de la herencia y del polimorfismo. En la clase base abstracta se define el procedimiento numérico que calcula la raíz de una ecuación trascendente, en las clases derivadas se tratan cada unos de los casos que van a surgir en el estudio de esta situación física aparente compleja.

Equilibrio de un elemento de la cuerda

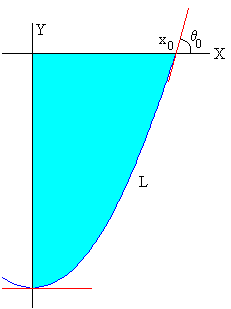
Una cuerda uniforme flexible de longitud 2L está sujeta a una varilla horizontal por sus extremos distantes 2x₀, tal como se muestra en la figura. Por razones de simetría respecto del eje Y, solamente analizaremos el comportamiento de la cuerda para x≥0.

Las fuerzas que actúan sobre un elemento ds de la cuerda son:

• El peso, λg·ds, donde λ es la masa por unidad de longitud de la cuerda.

• 2σ·ds, la fuerza debida a la tensión superficial,  donde σ  es el coeficiente de tensión superficial de la película jabonosa. El factor 2 se debe a que presenta dos caras.

• T+dT, es la fuerza que ejerce la parte derecha de la cuerda sobre el elemento ds, siendo θ+dθ el ángulo que forma con la horizontal.

• T, es la fuerza que ejerce la parte izquierda de la cuerda sobre el elemento ds, siendo θ el ángulo que forma con la horizontal.

Se pueden presentar los siguientes casos (véase la primera figura)

• Cuando la fuerza que ejerce la tensión superficial sobre el elemento ds,  2σ·ds (en color azul) es mayor que la componente del peso en la dirección normal λg·ds·cosθ (en color rojo), la cuerda es empujada hacia adentro, adoptando una configuración convexa (curvatura negativa).

• Cuando la fuerza que ejerce la tensión superficial sobre el elemento ds,  2σ·ds es menor que la componente del peso en la dirección normal λg·ds·cosθ, la cuerda es empujada hacia afuera, adoptando una configuración cóncava (curvatura positiva)

• Cuando ambas fuerza son iguales, la cuerda adopta una configuración lineal (curvatura cero)

Condiciones de equilibrio:

• A lo largo de la dirección tangencial

(T+dT)cos(dθ) =T+λg·ds·sinθ
dT= λg·ds·sinθ          (1)

• A lo largo de la dirección normal

(T+dT)sin(dθ)+2σ·ds =λg·ds·cosθ
T·dθ+2σ·ds =λg·ds·cosθ

${\displaystyle T=\lambda g\frac{ds}{d\theta }(\cos \theta -\alpha )\alpha =\frac{2\sigma }{\lambda g}}$                    (2)

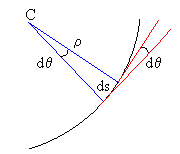En la figura, se muestra el significado del cociente ds/dθ. dθ es el ángulo que forman las rectas tangentes a la curva en la posición s y en la posición s+ds. dθ es el ángulo que forman las normales. Las direcciones normales se encuentran en un punto C denominado centro de curvatura, y ρ es el radio de curvatura, ds=ρ·dθ.

En la expresión (2), el ángulo θ está comprendido 0≤θ≤π/2 por tanto 0≤cosθ≤1. Por otra parte, la tensión de la cuerda T es siempre positiva.

• Si α>1, entonces ds/dθ<0  la cuerda adopta una forma convexa.

• Si α<1, hay tres posibilidades:

• Si cosθ>α entonces ds/dθ>0,  la cuerda adopta una forma cóncava

• Si cosθ<α entonces ds/dθ<0,  la cuerda adopta una forma convexa

• Si cosθ=α entonces ds/dθ=0, la cuerda adopta una forma lineal

Ahora bien, el ángulo θ varía a lo largo de la cuerda por lo que esta comparación no es satisfactoria.

Los parámetros más importantes de este sistema físico son α=2σ/λg, ya definido y el cociente x₀/L entre la separación de los extremos de la cuerda 2x₀ y la longitud de la cuerda 2L.

• En la configuración lineal θ es constante y cosθ=x₀/L.  Esta configuración se obtiene por tanto, cuando α=x₀/L.

• La configuración convexa se adopta cuando α>cosθ, (π/2<θ<θ₀) donde θ₀ es la tangente a la cuerda en su extremo x₀, es equivalente a α>x₀/L

• La configuración cóncava se adopta cuando α<cosθ, (0<θ<θ₀), es equivalente a α<x₀/L

Ecuación de curva que describe la forma que adopta la cuerda

Dividiendo las ecuaciones de equilibrio (1) y (2)

${\displaystyle \frac{dT}{T}=\frac{\sin \theta }{\cos \theta -\alpha }d\theta }$

Integrando

${\displaystyle \begin{array}{l}{\displaystyle \int \frac{dT}{T}}={\displaystyle \int \frac{\sin \theta }{\cos \theta -\alpha }d\theta }+\text{cte}\\ \ln T=-\ln (\cos \theta -\alpha )+\text{cte}\\ T(\cos \theta -\alpha )=C\lambda g\end{array}}$

donde C es una constante a determinar

Despejando T y sustituyéndola en la ecuación (2)

${\displaystyle \frac{ds}{d\theta }=\frac{C}{{\left(\cos \theta -\alpha \right)}^2}}$

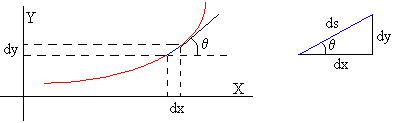Teniendo en cuenta que dx=ds·cosθ dy=ds·sinθ

Obtenemos las ecuaciones diferenciales de la curva dependiente del parámetro θ

${\displaystyle \frac{dx}{d\theta }=\frac{C·\cos \theta }{{\left(\cos \theta -\alpha \right)}^2}\frac{dy}{d\theta }=\frac{C·\text{sin}\theta }{{\left(\cos \theta -\alpha \right)}^2}}$

A continuación, vamos a integrar estas ecuaciones.

La segunda, se integra de forma inmediata

${\displaystyle y=C{\displaystyle \int \frac{\sin \theta }{{(\cos \theta -\alpha )}^2}}d\theta +C·c_y}$     

c_y es una constante de integración cuyo valor determinaremos más adelante.

Haciendo el cambio de variable

${\displaystyle \begin{array}{l}t=\cos \theta -\alpha dt=-\sin \theta ·d\theta \\ \frac{y}{C}={\displaystyle \int \frac{-dt}{t^2}}+c_y=\frac{1}{t}+c_y\end{array}}$

Deshaciendo el cambio

${\displaystyle \frac{y}{C}=\frac{1}{\cos \theta -\alpha }+c_y}$                       (3)

Más difícil resulta resolver la primera integral,

${\displaystyle \frac{x}{C}={\displaystyle \int \frac{\cos \theta }{{\left(\cos \theta -\alpha \right)}^2}d\theta }+c_x}$

c_x es una constante de integración cuyo valor determinaremos más adelante.

Se realiza el cambio de variable

${\displaystyle \begin{array}{l}t=\tan \left(\frac{\theta }{2}\right)dt=\frac{1}{2}(1+t^2)d\theta \\ \cos \theta =\frac{1-t^2}{1+t^2}\end{array}}$

La integral se convierte en

${\displaystyle \frac{1-t^2}{{(1-t^2-\alpha -\alpha t^2)}^2}dt}$

Se pueden presentar tres casos según que α>1, α<1 y α=1que conducen a distintos funciones integrando como veremos a continuación.

Caso α>1

Llamando

${\displaystyle \begin{array}{l}{\beta }^2=\frac{\alpha +1}{\alpha -1}>0\\ \frac{x}{C}=\frac{2}{{(\alpha -1)}^2}{\displaystyle \int \frac{1-t^2}{{\left(1+{\beta }^2{t}^2\right)}^2}dt}+c_x=\frac{2}{{(\alpha -1)}^2}{\displaystyle \int \frac{1+{\beta }^2{t}^2-{\beta }^2{t}^2-t^2}{{\left(1+{\beta }^2{t}^2\right)}^2}dt}+c_x=\\ \frac{2}{{(\alpha -1)}^2}\left\{{\displaystyle \int \frac{dt}{\left(1+{\beta }^2{t}^2\right)}}-(1+{\beta }^2){\displaystyle \int \frac{t^2}{{\left(1+{\beta }^2{t}^2\right)}^2}dt}\right\}+c_x\end{array}}$

La primera integral es inmediata y la segunda, procedemos a integrarla por partes

${\displaystyle {\displaystyle \int \frac{t^2}{{(1+{\beta }^2{t}^2)}^2}}dt=-\frac{1}{2{\beta }^2}\frac{t}{(1+{\beta }^2{t}^2)}+\frac{1}{2{\beta }^3}\arctan (\beta t)}$

El resultado final es

${\displaystyle \begin{array}{l}\frac{x}{C}=\frac{2}{{(\alpha -1)}^2}\left\{\frac{1}{\beta }\arctan (\beta t)-(1+{\beta }^2)\left(-\frac{1}{2{\beta }^2}\frac{t}{(1+{\beta }^2{t}^2)}+\frac{1}{2{\beta }^3}\arctan (\beta t)\right)\right\}+c_x=\\ \frac{2}{{(\alpha -1)}^2{\beta }^2}\left\{\frac{{\beta }^2-1}{\beta }\arctan (\beta t)+\frac{(1+{\beta }^2)t}{(1+{\beta }^2{t}^2)}\right\}+c_x\end{array}}$

Ahora, se deshace los cambios se expresa t en función del ángulo θ, y β en función de α.

${\displaystyle \cos \theta =\frac{1-t^2}{1+t^2}{t}^2=\frac{1-\cos \theta }{1+\cos \theta }=\frac{{(1-\cos \theta )}^2}{{\sin }^2\theta }t=\frac{1-\cos \theta }{\sin \theta }}$

El resultado final es

${\displaystyle \frac{x}{C}=\frac{1}{{\alpha }^2-1}\left\{\frac{2}{\sqrt{{\alpha }^2-1}}\arctan \left(\frac{\alpha +1}{\sqrt{{\alpha }^2-1}}\tan \left(\frac{\theta }{2}\right)\right)+\frac{\alpha \sin \theta }{\alpha -\cos \theta }\right\}+c_x}$          (4)

Caso α<1

Llamando

${\displaystyle \begin{array}{l}{\beta }^2=\frac{1+\alpha }{1-\alpha }>0\\ \frac{x}{C}=\frac{2}{{(1-\alpha )}^2}{\displaystyle \int \frac{1-t^2}{{\left(1-{\beta }^2{t}^2\right)}^2}dt}+c_x=\frac{2}{{(1-\alpha )}^2}{\displaystyle \int \frac{1-{\beta }^2{t}^2+{\beta }^2{t}^2-t^2}{{\left(1-{\beta }^2{t}^2\right)}^2}dt}+c_x=\\ \frac{2}{{(1-\alpha )}^2}\left\{{\displaystyle \int \frac{dt}{\left(1-{\beta }^2{t}^2\right)}}+({\beta }^2-1){\displaystyle \int \frac{t^2}{{\left(1-{\beta }^2{t}^2\right)}^2}dt}\right\}+c_x\end{array}}$

El resultado de la primera integral es

${\displaystyle {\displaystyle \int \frac{dt}{1-{\beta }^2{t}^2}}=\frac{1}{2}{\displaystyle \int \frac{dt}{1+\beta t}}+\frac{1}{2}{\displaystyle \int \frac{dt}{1-\beta t}}=\frac{1}{2\beta }\ln \left|\frac{1+\beta t}{1-\beta t}\right|}$

La segunda, la integramos por partes

${\displaystyle {\displaystyle \int \frac{t^2}{{\left(1-{\beta }^2{t}^2\right)}^2}}dt=\frac{1}{2{\beta }^2}\frac{t}{(1-{\beta }^2{t}^2)}-\frac{1}{2\beta }{\displaystyle \int \frac{dt}{1-{\beta }^2{t}^2}}=\frac{1}{2{\beta }^2}\frac{t}{(1-{\beta }^2{t}^2)}-\frac{1}{4{\beta }^3}\ln \left|\frac{1+\beta t}{1-\beta t}\right|}$

El resultado final es

${\displaystyle \frac{x}{C}=\frac{1}{{(1-\alpha )}^2{\beta }^2}\left\{\frac{{\beta }^2+1}{2\beta }\ln \left|\frac{1+\beta t}{1-\beta t}\right|+({\beta }^2-1)\frac{t}{1-{\beta }^2{t}^2}\right\}+c_x}$

Ahora, se deshace los cambios se expresa t en función del ángulo θ, y β en función de α.

${\displaystyle \cos \theta =\frac{1-t^2}{1+t^2}{t}^2=\frac{1-\cos \theta }{1+\cos \theta }=\frac{{(1-\cos \theta )}^2}{{\sin }^2\theta }t=\frac{1-\cos \theta }{\sin \theta }}$

El resultado final es

${\displaystyle \frac{x}{C}=\frac{1}{1-{\alpha }^2}\left\{\frac{1}{\sqrt{{\alpha }^2-1}}\ln \left|\frac{\sqrt{1-{\alpha }^2}+(1+\alpha )\tan (\theta /2)}{\sqrt{1-{\alpha }^2}-(1+\alpha )\tan (\theta /2)}\right|+\frac{\alpha \sin \theta }{\cos \theta -\alpha }\right\}+c_x}$                 (5)

Caso α=1

${\displaystyle \frac{x}{C}=2{\displaystyle \int \frac{1-t^2}{{\left(-2t^2\right)}^2}dt}+c_x=\frac{1}{2}{\displaystyle \int \left(\frac{1}{t^4}-\frac{1}{t^2}\right)dt}+c_x=\frac{1}{2}\left(\frac{-1}{3t^3}+\frac{1}{t}\right)+c_x}$

Deshaciendo los cambios

t=tan(θ/2)

${\displaystyle \frac{x}{C}=\frac{-1}{6{\tan }^3(\theta /2)}+\frac{1}{2\tan (\theta /2)}+c_x}$                (6)

Configuración lineal

Este caso especial, se produce cuando cosθ=α=x₀/L.

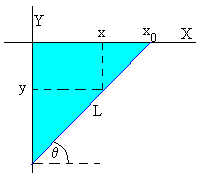Como el ángulo θ es constante, la cuerda adopta la forma de un segmento de recta cuya ecuación es ${\displaystyle y=(x-x_0)\tan \theta =\frac{\sqrt{L^2-x_0^2}}{x_0}(x-x_0)}$

Configuración cóncava

La cuerda adopta una configuración cóncava cuando α<x₀/L, naturalmente α<1

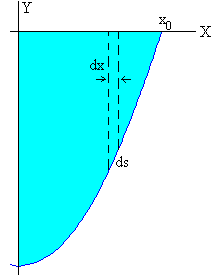
La configuración cóncava es similar en su forma a la catenaria, presentando un mínimo (vértice) en x=0. Para x=0, la recta tangente a la cuerda en el vértice forma un ángulo θ=0 Para x=x0, la recta tangente a la cuerda en el extremo forma un ángulo θ=θ0.

Las ecuaciones paramétricas de la curva son (3) y (5)

${\displaystyle \begin{array}{l}\frac{x}{C}=\frac{1}{1-{\alpha }^2}\left\{\frac{1}{\sqrt{{\alpha }^2-1}}\ln \left|\frac{\sqrt{1-{\alpha }^2}+(1+\alpha )\tan (\theta /2)}{\sqrt{1-{\alpha }^2}-(1+\alpha )\tan (\theta /2)}\right|+\frac{\alpha \sin \theta }{\cos \theta -\alpha }\right\}+c_x\\ \frac{y}{C}=\frac{1}{\cos \theta -\alpha }+c_y\end{array}}$

• Para x=0, la recta tangente a la cuerda en el vértice forma un ángulo θ=0

• Para y=0, recta tangente a la cuerda en el extremo forma un ángulo θ=θ₀.

Con estos dos datos determinamos las constantes de integración c_x y c_y

${\displaystyle \begin{array}{l}\frac{x}{C}=\frac{1}{1-{\alpha }^2}\left\{\frac{1}{\sqrt{{\alpha }^2-1}}\ln \left|\frac{\sqrt{1-{\alpha }^2}+(1+\alpha )\tan (\theta /2)}{\sqrt{1-{\alpha }^2}-(1+\alpha )\tan (\theta /2)}\right|+\frac{\alpha \sin \theta }{\cos \theta -\alpha }\right\}\\ \frac{y}{C}=\frac{1}{\cos \theta -\alpha }-\frac{1}{\cos {\theta }_0-\alpha }\end{array}}$

Para representar la curva que describe la forma que adopta la cuerda, necesitamos conocer la constante C y el ángulo θ₀.

Cálculo de la constante C y del ángulo θ₀.

La longitud de la mitad de la cuerda L, se obtiene integrando ${\displaystyle L={\displaystyle \underset{0}{\overset{L}{\int }}ds}=C{\displaystyle \underset{0}{\overset{{\theta }_0}{\int }}\frac{d\theta }{{\left(\cos \theta -\alpha \right)}^2}}}$ Para resolver esta integral seguimos los mismos pasos que para obtener la abscisa x en función del parámetro θ.

Se realiza el cambio de variable

${\displaystyle \begin{array}{l}t=\tan \left(\frac{\theta }{\text{2}}\right)dt=\frac{1}{2}(1+t^2)d\theta \\ \cos \theta =\frac{1-t^2}{1+t^2}\end{array}}$

La integral se convierte en

${\displaystyle \begin{array}{l}\frac{L}{C}=\frac{2}{{(1-\alpha )}^2}{\displaystyle \underset{t_0}{\overset{t_1}{\int }}\frac{1+t^2}{{\left(1+\frac{\alpha +1}{\alpha -1}{t}^2\right)}^2}dt}=\frac{2}{{(1-\alpha )}^2}{\displaystyle \underset{t_0}{\overset{t_1}{\int }}\frac{1+t^2}{{\left(1-{\beta }^2{t}^2\right)}^2}dt}{\beta }^2=\frac{1+\alpha }{1-\alpha }\\ \frac{L}{C}=\frac{2}{{(1-\alpha )}^2}{\displaystyle \underset{t_0}{\overset{t_1}{\int }}\frac{1-{\beta }^2{t}^2+{\beta }^2{t}^2+t^2}{{\left(1-{\beta }^2{t}^2\right)}^2}dt}=\frac{2}{{(1-\alpha )}^2}\left\{{\displaystyle \underset{t_0}{\overset{t_1}{\int }}\frac{dt}{\left(1-{\beta }^2{t}^2\right)}}+({\beta }^2+1){\displaystyle \underset{t_0}{\overset{t_1}{\int }}\frac{t^2}{{\left(1-{\beta }^2{t}^2\right)}^2}dt}\right\}=\\ {\frac{1}{{(1-\alpha )}^2{\beta }^2}\left\{\frac{{\beta }^2-1}{2\beta }\ln \left|\frac{1+\beta t}{1-\beta t}\right|+({\beta }^2+1)\frac{t}{1-{\beta }^2{t}^2}\right\}|}_{t_0}^{t_1}\end{array}}$

Deshaciendo los cambios  obtenemos

${\displaystyle \begin{array}{l}\frac{L}{C}={\frac{1}{1-{\alpha }^2}\left\{\frac{\alpha }{\sqrt{{\alpha }^2-1}}\ln \left|\frac{\sqrt{1-{\alpha }^2}+(1+\alpha )\tan (\theta /2)}{\sqrt{1-{\alpha }^2}-(1+\alpha )\tan (\theta /2)}\right|+\frac{\sin \theta }{\cos \theta -\alpha }\right\}|}_0^{{\theta }_0}\\ \frac{L}{C}=\frac{1}{1-{\alpha }^2}\left\{\frac{\alpha }{\sqrt{{\alpha }^2-1}}\ln \left|\frac{\sqrt{1-{\alpha }^2}+(1+\alpha )\tan ({\theta }_0/2)}{\sqrt{1-{\alpha }^2}-(1+\alpha )\tan ({\theta }_0/2)}\right|+\frac{\sin {\theta }_0}{\cos {\theta }_0-\alpha }\right\}\end{array}}$

La posición del extremo de la cuerda es x₀ y el ángulo que forma la recta tangente en este punto es θ₀ (véase la figura)

${\displaystyle \frac{x_0}{C}=\frac{1}{1-{\alpha }^2}\left\{\frac{1}{\sqrt{{\alpha }^2-1}}\ln \left|\frac{\sqrt{1-{\alpha }^2}+(1+\alpha )\tan ({\theta }_0/2)}{\sqrt{1-{\alpha }^2}-(1+\alpha )\tan ({\theta }_0/2)}\right|+\frac{\alpha \sin {\theta }_0}{\cos {\theta }_0-\alpha }\right\}}$

Se elimina C en estas dos últimas ecuaciones, obteniendo una ecuación trascendente en θ₀. En la figura, vemos que para α=0.3<x₀/L=0.5 dicha ecuación tiene un cero en un ángulo próximo a 70º, y presenta una discontinuidad para el ángulo tal que

${\displaystyle \sqrt{1-{\alpha }^2}=(1+\alpha )\tan \left(\theta /2\right)}$

Para α=0.3, θ=72.5º

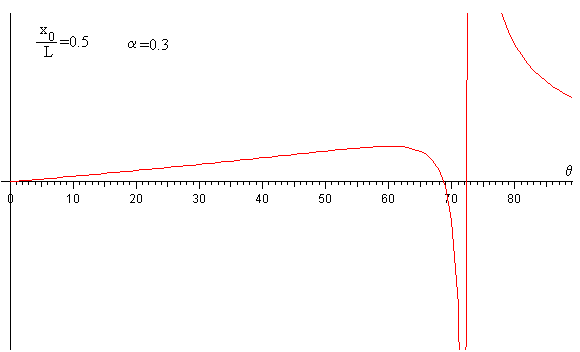
Se resuelve la ecuación trascendente en el intervalo (0, 72.5º) por el procedimiento numérico del punto medio, obteniéndose el ángulo θ₀=68.7º que forma la tangente a la cuerda en el extremo x₀=1.

Una vez que se ha determinado θ₀, se calcula C y se representa las ecuaciones paramétricas x(θ), y(θ) en el intervalo 0≤θ≤θ₀.

Configuración convexa

Hay tres posibles configuraciones convexas.

• α>x₀/L con α<1

• α>1

• α=1

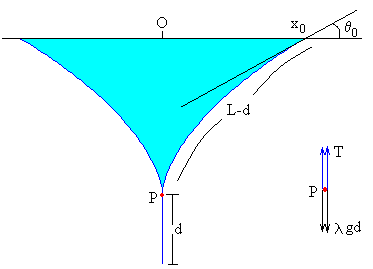
La configuración convexa tiene la particularidad de que una longitud d de la cuerda por debajo del vértice P está pegada a la porción d del otro lado del eje Y. Una porción L-d de la cuerda forma el arco convexo a cada uno de los lados de dicho eje. La recta tangente a la cuerda forma ángulos θ comprendidos entre π/2 y θ₀.

Del punto P, cuelga una longitud d de la cuerda por cada lado, la tensión de la cuerda en este punto es

T=λgd

Deducimos por integración una expresión para la tensión de la cuerda en función del parámetro θ,

T(cosθ-α)=Cλg

En el punto P, para θ=π/2 se obtiene

-Tα=Cλg

El valor de la constante C=-αd

Primer caso, α>x₀/L con α<1

Este caso es similar al cóncavo

Las ecuaciones paramétricas de la cuerda son (3) y (5)

${\displaystyle \begin{array}{l}\frac{x}{C}=\frac{1}{1-{\alpha }^2}\left\{\frac{1}{\sqrt{{\alpha }^2-1}}\ln \left|\frac{\sqrt{1-{\alpha }^2}+(1+\alpha )\tan (\theta /2)}{\sqrt{1-{\alpha }^2}-(1+\alpha )\tan (\theta /2)}\right|+\frac{\alpha \sin \theta }{\cos \theta -\alpha }\right\}+c_x\\ \frac{y}{C}=\frac{1}{\cos \theta -\alpha }+c_y\end{array}}$

• Para x=0, el ángulo que forma la recta tangente a la cuerda es θ= π/2.

• Para y=0, el ángulo que forma la recta tangente a la cuerda es θ=θ₀

Con estos dos datos determinamos las constantes de integración c_x y c_y.

${\displaystyle \begin{array}{l}\frac{x}{-\alpha d}=\frac{1}{1-{\alpha }^2}\left\{\begin{array}{l}\frac{1}{\sqrt{{\alpha }^2-1}}\ln \left|\frac{\sqrt{1-{\alpha }^2}+(1+\alpha )\tan (\theta /2)}{\sqrt{1-{\alpha }^2}-(1+\alpha )\tan (\theta /2)}\right|+\frac{\alpha \sin \theta }{\cos \theta -\alpha }\\ -\frac{1}{\sqrt{{\alpha }^2-1}}\ln \left|\frac{\sqrt{1-{\alpha }^2}+(1+\alpha )}{\sqrt{1-{\alpha }^2}-(1+\alpha )}\right|+1\end{array}\right\}\\ \frac{y}{-\alpha d}=\frac{1}{\cos \theta -\alpha }-\frac{1}{\cos {\theta }_0-\alpha }\end{array}}$

Para representar la curva que describe la forma que adopta la cuerda, necesitamos conocer la longitud d y el ángulo θ₀.

Cálculo de la longitud d y del ángulo θ₀.

La longitud de la mitad de la cuerda L, se obtiene integrando

${\displaystyle L-d={\displaystyle \underset{0}{\overset{L-d}{\int }}ds}=C{\displaystyle \underset{\pi /2}{\overset{{\theta }_0}{\int }}\frac{d\theta }{{\left(\cos \theta -\alpha \right)}^2}}=\alpha d{\displaystyle \underset{{\theta }_0}{\overset{\pi /2}{\int }}\frac{d\theta }{{\left(\cos \theta -\alpha \right)}^2}}}$

Ya hemos obtenido en la configuración cóncava el valor del integrando

${\displaystyle \begin{array}{l}\frac{L-d}{\alpha d}={\frac{1}{1-{\alpha }^2}\left\{\frac{\alpha }{\sqrt{{\alpha }^2-1}}\ln \left|\frac{\sqrt{1-{\alpha }^2}+(1+\alpha )\tan (\theta /2)}{\sqrt{1-{\alpha }^2}-(1+\alpha )\tan (\theta /2)}\right|+\frac{\sin \theta }{\cos \theta -\alpha }\right\}|}_{{\theta }_0}^{\pi /2}=\\ \frac{L}{\alpha d}-\frac{1}{\alpha }=\frac{1}{1-{\alpha }^2}\left\{\begin{array}{l}\frac{\alpha }{\sqrt{{\alpha }^2-1}}\ln \left|\frac{\sqrt{1-{\alpha }^2}+(1+\alpha )}{\sqrt{1-{\alpha }^2}-(1+\alpha )}\right|-\frac{1}{\alpha }\\ -\frac{\alpha }{\sqrt{{\alpha }^2-1}}\ln \left|\frac{\sqrt{1-{\alpha }^2}+(1+\alpha )\tan ({\theta }_0/2)}{\sqrt{1-{\alpha }^2}-(1+\alpha )\tan ({\theta }_0/2)}\right|-\frac{\sin {\theta }_0}{\cos {\theta }_0-\alpha }\end{array}\right\}\\ \frac{L}{\alpha d}=\frac{1}{1-{\alpha }^2}\left\{\begin{array}{l}\frac{\alpha }{\sqrt{{\alpha }^2-1}}\ln \left|\frac{\sqrt{1-{\alpha }^2}+(1+\alpha )}{\sqrt{1-{\alpha }^2}-(1+\alpha )}\right|-\alpha \\ -\frac{\alpha }{\sqrt{{\alpha }^2-1}}\ln \left|\frac{\sqrt{1-{\alpha }^2}+(1+\alpha )\tan ({\theta }_0/2)}{\sqrt{1-{\alpha }^2}-(1+\alpha )\tan ({\theta }_0/2)}\right|-\frac{\sin {\theta }_0}{\cos {\theta }_0-\alpha }\end{array}\right\}\end{array}}$

La posición del extremo de la cuerda es x₀ y el ángulo que forma la recta tangente a la cuerda en este punto es θ₀.

${\displaystyle \frac{x_0}{-\alpha d}=\frac{1}{1-{\alpha }^2}\left\{\begin{array}{l}\frac{1}{\sqrt{{\alpha }^2-1}}\ln \left|\frac{\sqrt{1-{\alpha }^2}+(1+\alpha )\tan ({\theta }_0/2)}{\sqrt{1-{\alpha }^2}-(1+\alpha )\tan ({\theta }_0/2)}\right|+\frac{\alpha \sin {\theta }_0}{\cos {\theta }_0-\alpha }\\ -\frac{1}{\sqrt{{\alpha }^2-1}}\ln \left|\frac{\sqrt{1-{\alpha }^2}+(1+\alpha )}{\sqrt{1-{\alpha }^2}-(1+\alpha )}\right|+1\end{array}\right\}}$

Se elimina d en estas dos últimas ecuaciones, obteniendo una ecuación trascendente en θ₀. En la figura, vemos que para α=0.7>x₀/L=0.5 y α<1. Dicha ecuación tiene un cero en un ángulo próximo a 50º y presenta una discontinuidad para el ángulo tal que

${\displaystyle \sqrt{1-{\alpha }^2}=(1+\alpha )\tan \left(\theta /2\right)}$

Para α=0.7, θ=45.6º

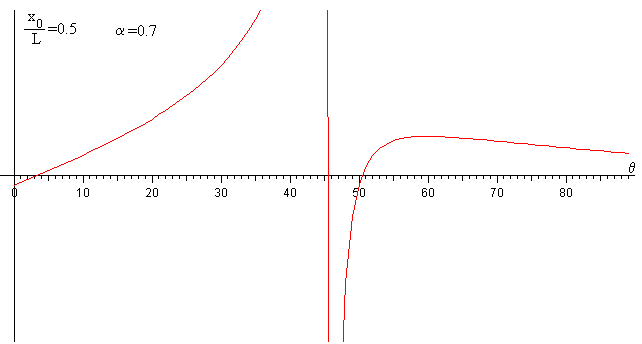
Se resuelve la ecuación trascendente, por el procedimiento numérico del punto medio, en el intervalo (45.6, 90º) obteniéndose el ángulo θ₀=50.5º que forma la tangente a la cuerda en el extremo x₀=1.

Una vez que se ha determinado θ₀, se calcula d y se representa las ecuaciones paramétricas x(θ), y(θ) en el intervalo θ₀≤θ≤π/2

Segundo caso, α>1

Las ecuaciones paramétricas de la cuerda son (3) y (4)

${\displaystyle \begin{array}{l}\frac{x}{C}=\frac{1}{{\alpha }^2-1}\left\{\frac{2}{\sqrt{{\alpha }^2-1}}\arctan \left(\frac{\alpha +1}{\sqrt{{\alpha }^2-1}}\tan \left(\frac{\theta }{2}\right)\right)+\frac{\alpha \sin \theta }{\alpha -\cos \theta }\right\}+c_x\\ \frac{y}{C}=\frac{1}{\cos \theta -\alpha }+c_y\end{array}}$

con C=-αd como en el caso anterior

• Para x=0, el ángulo que forma la recta tangente a la cuerda es θ= π/2.

• Para y=0, el ángulo que forma la recta tangente a la cuerda es θ=θ₀

Con estos dos datos determinamos las constantes de integración c_x y c_y.

${\displaystyle \begin{array}{l}\frac{x}{-\alpha d}=\frac{1}{{\alpha }^2-1}\left\{\begin{array}{l}\frac{2}{\sqrt{{\alpha }^2-1}}\arctan \left(\frac{\alpha +1}{\sqrt{{\alpha }^2-1}}\tan \left(\frac{\theta }{2}\right)\right)+\frac{\alpha \sin \theta }{\alpha -\cos \theta }\\ -\frac{2}{\sqrt{{\alpha }^2-1}}\arctan \left(\frac{\alpha +1}{\sqrt{{\alpha }^2-1}}\right)-1\end{array}\right\}\\ \frac{y}{-\alpha d}=\frac{1}{\cos \theta -\alpha }-\frac{1}{\cos {\theta }_0-\alpha }\end{array}}$

Para representar la curva que describe la forma que adopta la cuerda, necesitamos conocer la longitud d y el ángulo θ₀.

Cálculo de la longitud d y del ángulo θ₀.

La longitud de la mitad de la cuerda L, se obtiene integrando

${\displaystyle L-d={\displaystyle \underset{0}{\overset{L-d}{\int }}ds}=C{\displaystyle \underset{\pi /2}{\overset{{\theta }_0}{\int }}\frac{d\theta }{{\left(\cos \theta -\alpha \right)}^2}}=\alpha d{\displaystyle \underset{{\theta }_0}{\overset{\pi /2}{\int }}\frac{d\theta }{{\left(\cos \theta -\alpha \right)}^2}}}$

Se realiza el cambio de variable

${\displaystyle \begin{array}{l}t=\tan \left(\frac{\theta }{2}\right)dt=\frac{1}{2}(1+t^2)d\theta \\ \cos \theta =\frac{1-t^2}{1+t^2}\end{array}}$

La integral se convierte en

${\displaystyle \begin{array}{l}\frac{L-d}{\alpha d}=\frac{2}{{(\alpha -1)}^2}{\displaystyle \underset{t_0}{\overset{t_1}{\int }}\frac{1+t^2}{{\left(1+\frac{\alpha +1}{\alpha -1}{t}^2\right)}^2}dt}=\frac{2}{{(\alpha -1)}^2}{\displaystyle \underset{t_0}{\overset{t_1}{\int }}\frac{1+t^2}{{\left(1+{\beta }^2{t}^2\right)}^2}dt}{\beta }^2=\frac{\alpha +1}{\alpha -1}\\ \frac{L-d}{\alpha d}=\frac{2}{{(\alpha -1)}^2}{\displaystyle \underset{t_0}{\overset{t_1}{\int }}\frac{1+{\beta }^2{t}^2-{\beta }^2{t}^2+t^2}{{\left(1+{\beta }^2{t}^2\right)}^2}dt}=\frac{2}{{(\alpha -1)}^2}\left\{{\displaystyle \underset{t_0}{\overset{t_1}{\int }}\frac{dt}{\left(1+{\beta }^2{t}^2\right)}}+(1-{\beta }^2){\displaystyle \underset{t_0}{\overset{t_1}{\int }}\frac{t^2}{{\left(1+{\beta }^2{t}^2\right)}^2}dt}\right\}=\end{array}}$

La primera integral es inmediata y la segunda procedemos a integrarla por partes

${\displaystyle {\displaystyle \int \frac{t^2}{{\left(1+{\beta }^2{t}^2\right)}^2}}dt=-\frac{1}{2{\beta }^2}\frac{t}{(1+{\beta }^2{t}^2)}+\frac{1}{2{\beta }^3}\arctan (\beta t)}$

El resultado final es

${\displaystyle \begin{array}{l}\frac{L-d}{\alpha d}={\frac{2}{{(\alpha -1)}^2}\left\{\frac{1}{\beta }\arctan (\beta t)+(1-{\beta }^2)\left(-\frac{1}{2{\beta }^2}\frac{t}{(1+{\beta }^2{t}^2)}+\frac{1}{2{\beta }^3}\arctan (\beta t)\right)\right\}|}_{t_1}^{t_2}=\\ {\frac{2}{{(\alpha -1)}^2{\beta }^2}\left\{\frac{{\beta }^2+1}{\beta }\arctan (\beta t)+\frac{({\beta }^2-1)t}{(1+{\beta }^2{t}^2)}\right\}|}_{t_1}^{t_2}\end{array}}$

Ahora, se deshace los cambios se expresa t en función del ángulo θ, y β en función de α.

${\displaystyle \cos \theta =\frac{1-t^2}{1+t^2}{t}^2=\frac{1-\cos \theta }{1+\cos \theta }=\frac{{(1-\cos \theta )}^2}{{\sin }^2\theta }t=\frac{1-\cos \theta }{\sin \theta }}$

El resultado final es

${\displaystyle \begin{array}{l}\frac{L}{\alpha d}-\frac{1}{\alpha }={\frac{1}{{\alpha }^2-1}\left\{\frac{2\alpha }{\sqrt{{\alpha }^2-1}}\arctan \left(\frac{\alpha +1}{\sqrt{{\alpha }^2-1}}\tan \left(\frac{\theta }{2}\right)\right)+\frac{\sin \theta }{\alpha -\cos \theta }\right\}|}_{{\theta }_0}^{\pi /2}\\ =\frac{1}{{\alpha }^2-1}\left\{\frac{2\alpha }{\sqrt{{\alpha }^2-1}}\arctan \left(\frac{\alpha +1}{\sqrt{{\alpha }^2-1}}\right)+\frac{1}{\alpha }-\frac{2\alpha }{\sqrt{{\alpha }^2-1}}\arctan \left(\frac{\alpha +1}{\sqrt{{\alpha }^2-1}}\tan \left(\frac{{\theta }_0}{2}\right)\right)-\frac{\sin {\theta }_0}{\alpha -\cos {\theta }_0}\right\}\\ \frac{L}{\alpha d}=\frac{1}{{\alpha }^2-1}\left\{\frac{2\alpha }{\sqrt{{\alpha }^2-1}}\arctan \left(\frac{\alpha +1}{\sqrt{{\alpha }^2-1}}\right)+\alpha -\frac{2\alpha }{\sqrt{{\alpha }^2-1}}\arctan \left(\frac{\alpha +1}{\sqrt{{\alpha }^2-1}}\tan \left(\frac{{\theta }_0}{2}\right)\right)-\frac{\sin {\theta }_0}{\alpha -\cos {\theta }_0}\right\}\end{array}}$

La posición del extremo de la cuerda es x₀ y el ángulo que forma la recta tangente a la cuerda en este punto es θ₀.

${\displaystyle \frac{x_0}{-\alpha d}=\frac{1}{{\alpha }^2-1}\left\{\begin{array}{l}\frac{2}{\sqrt{{\alpha }^2-1}}\arctan \left(\frac{\alpha +1}{\sqrt{{\alpha }^2-1}}\tan \left(\frac{{\theta }_0}{2}\right)\right)+\frac{\alpha \sin {\theta }_0}{\alpha -\cos {\theta }_0}\\ -\frac{2}{\sqrt{{\alpha }^2-1}}\arctan \left(\frac{\alpha +1}{\sqrt{{\alpha }^2-1}}\right)-1\end{array}\right\}}$

Se elimina d en estas dos últimas ecuaciones, obteniendo una ecuación trascendente en θ₀. En la figura, vemos que para α=1.2 la ecuación presenta un cero para un ángulo próximo a 31.º

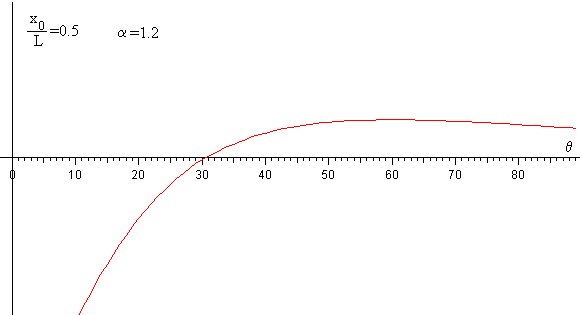
Se resuelve la ecuación trascendente, por el procedimiento numérico del punto medio, obteniéndose el ángulo θ₀=30.7º que forma la tangente a la cuerda en el extremo x₀=1.

Una vez que se ha determinado θ₀, se calcula d y se representa las ecuaciones paramétricas x(θ), y(θ) en el intervalo θ₀≤θ≤π/2

Tercer caso, α=1

Las ecuaciones paramétricas de la cuerda son (3) y (6)

${\displaystyle \begin{array}{l}\frac{x}{C}=\frac{1}{6\tan (\theta /2)}\left(4-\frac{1}{{\sin }^2(\theta /2)}\right)+c_x\\ \frac{y}{C}=\frac{1}{\cos \theta -1}+c_y\end{array}}$

con C=-αd=-d como en el caso anterior

• Para x=0, el ángulo que forma la recta tangente a la cuerda es θ= π/2.

• Para y=0, el ángulo que forma la recta tangente a la cuerda es θ=θ₀

Con estos dos datos determinamos las constantes de integración c_x y c_y.

${\displaystyle \begin{array}{l}\frac{x}{-d}=\frac{-1}{6{\tan }^3(\theta /2)}+\frac{1}{2\tan (\theta /2)}-\frac{1}{3}\\ \frac{y}{-d}=\frac{1}{\cos \theta -1}-\frac{1}{\cos {\theta }_0-1}\end{array}}$

Para representar la curva que describe la forma que adopta la cuerda, necesitamos conocer la longitud d y el ángulo θ₀.

Cálculo de la longitud d y del ángulo θ₀.

La longitud de la mitad de la cuerda L, se obtiene integrando

${\displaystyle L-d={\displaystyle \underset{0}{\overset{L-d}{\int }}ds}=C{\displaystyle \underset{\pi /2}{\overset{{\theta }_0}{\int }}\frac{d\theta }{{\left(\cos \theta -1\right)}^2}}=d{\displaystyle \underset{{\theta }_0}{\overset{\pi /2}{\int }}\frac{d\theta }{{\left(\cos \theta -1\right)}^2}}}$

Se realiza el cambio de variable

${\displaystyle \begin{array}{l}t=\tan \left(\frac{\theta }{2}\right)dt=\frac{1}{2}(1+t^2)d\theta \\ \cos \theta =\frac{1-t^2}{1+t^2}\\ L-d=2d{\displaystyle \underset{t_0}{\overset{t_1}{\int }}\frac{1+t^2}{{\left(-2t^2\right)}^2}dt}=\frac{d}{2}{\displaystyle \underset{t_0}{\overset{t_1}{\int }}\left(\frac{1}{t^4}+\frac{1}{t^2}\right)dt}={\frac{d}{2}\left(\frac{-1}{3t^3}-\frac{1}{t}\right)|}_{t_0}^{t_1}\end{array}}$

Deshaciendo los cambios

${\displaystyle \begin{array}{l}L-d={-\frac{d}{2}\left(\frac{1}{3{\tan }^3(\theta /2)}+\frac{1}{\tan (\theta /2)}\right)|}_{{\theta }_0}^{\pi /2}\\ \frac{L}{d}=\frac{1}{6{\tan }^3({\theta }_0/2)}+\frac{1}{2\tan ({\theta }_0/2)}+\frac{1}{3}\end{array}}$

La posición del extremo de la cuerda es x₀ y el ángulo que forma la recta tangente a la cuerda en este punto es θ₀.

${\displaystyle \frac{x_0}{d}=\frac{1}{6{\tan }^3({\theta }_0/2)}-\frac{1}{2\tan ({\theta }_0/2)}+\frac{1}{3}}$

Se elimina d en estas dos últimas ecuaciones, obteniendo una ecuación trascendente en θ₀. En la figura, vemos que para α=1, la ecuación presenta un cero para un ángulo próximo a 38.º

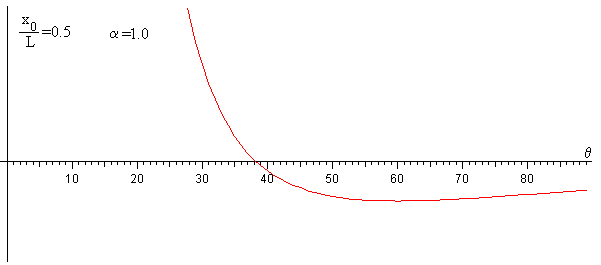
Se resuelve la ecuación trascendente, por el procedimiento numérico del punto medio, obteniéndose el ángulo θ₀=38.3º que forma la tangente a la cuerda en el extremo x₀=1.

Una vez que se ha determinado θ₀, se calcula d y se representa las ecuaciones paramétricas x(θ), y(θ) en el intervalo θ₀≤θ≤π/2

Actividades

Se introduce

• El cociente x₀/L<1 (distancia 2x₀ entre los extremos de la cuerda, entre la longitud 2L de la cuerda)  actuando en la barra de desplazamiento titulada  x0/L

• El valor del parámetro α, actuando en la barra de desplazamiento titulada Alfa

• Se ha fijado la longitud de la mitad de la cuerda en el valor L=2.0

Se pulsa el botón titulado Gráfica

Se dibuja la forma que adopta la cuerda, se proporciona los datos de la ordenada y_min del vértice, para x=0, y en el caso de las configuraciones convexas, la longitud d de la parte de la cuerda que permanece pegada debajo del vértice. Sus abscisas son x=0 y sus ordenadas varían entre y_min e y_min+d.

Fijado el valor de α, se observa el efecto de la modificación de la distancia 2x₀ entre los extremos de la cuerda sujetos a la varilla horizontal.

Fijado el valor de la distancia 2x₀ entre los extremos de la cuerda, se modifica el valor del parámetro α=2σ/λg. Simulando cuerdas de distintas densidades λ o películas jabonosas de distinto coeficiente de tensión superficial σ.

Se dibuja

• En color azul, la fuerza que ejerce la tensión superficial por unidad de longitud, 2σ

• En color negro, el peso de la cuerda por unidad del longitud, λg

• En color rojo, la componente del peso, en la dirección normal, λg·cosθ

Se cambia la ordenada y del punto de la cuerda en el que se dibujan las fuerzas, actuando en la barra de desplazamiento titulada Posición.

Se compara la longitud del vector de color azul (tensión superficial) con el vector de color rojo (componente del peso).

CalibreApplet aparecerá en un explorador compatible con JDK 1.1.

Referencias

Behroozi F., Mohazzabi P., McCrickard J. P., Remarkable shapes of a catenary under the effect of gravity and surface tension. Am. J. Phys. 62 (12) December 1994, pp. 1121-1128.

Curso Interactivo de Física en Internet © Ángel Franco García