Funciones recursivas. Fractales
Se denominan funciones recursivas a aquellas que se llaman a sí mismas. Un ejemplo típico es el método de ordenación quick-sort, el juego denominado Torres de Hanoi, etc.
Hay varios casos de funciones recursivas que se emplean en la Física, las funciones de Bessel, los polinomios de Hermite, etc.
Empezaremos por distinguir un método iterativo frente a un método recursivo mediante el ejemplo del cálculo del factorial de un número n.
n!=n·(n-1)·(n-2)...2·1
El resultado del factorial de un número entero es un número entero mucho más grande (long), que puede sobrepasar el rango de los enteros (int) si n es grande.
- Método iterativo
long factorial(int n){
long resultado=1;
for(int i=1; i<=n; i++){
resultado*=i;
}
return resultado;
}
- Método recursivo
long factorial(int n){
if(n==0) return 1;
return (n*factorial(n-1));
}
La geometría de la Tortuga
En primer lugar, creamos una clase que denominaremos Tortuga, por su similitud con la tortuga del lenguaje LOGO, tan popular a mediados de los años 80, en la que definiremos varios métodos que ejecutan movimientos o trazados simples. Una vez definidos los movimientos básicos en la clase Tortuga es posible crear rutinas recursivas que dibujen distintos motivos a escalas diferentes.
El estado de la tortuga, se especifica por su posición x e y y por su ángulo de orientación respecto del eje horizontal X. También podemos asignar a la tortuga un color (rojo, azul o verde)
Los distintos comandos que cambian el estado de la tortuga se seleccionan pulsando en tres botones de radio:
Inicia, sitúa a la tortuga en una posición x e y especificada, orientando la tortuga a lo largo del eje X (ángulo cero).
Gira, cambia la orientación de la tortuga, sumando a su dirección actual, el ángulo que seleccionamos en la barra de desplazamiento. Los posibles ángulos van desde –180º a 180º.
Mueve, desplaza la tortuga una distancia especificada a lo largo de su dirección. Se puede mover la tortuga sin que deje una traza o se puede mover de modo que deje una traza del color seleccionado. Para que dibuje su trayectoria, se activa la casilla titulada Lápiz.
El botón Nuevo borra la trayectoria de la tortuga y da comienzo a una nueva experiencia, situando a la tortuga en el origen, orientada a lo largo del eje X (ángulo cero).
El botón titulado Aplicar ejecuta cada uno de los tres comandos que se definen pulsando en cada uno de los tres botones de radio, e introduciendo los datos requeridos.
Ejemplos:
- Para trazar un cuadrado de lado 100 unidades.
Inicia X: -50, Y:50 → se pulsa el botón Aplicar
Mueve 100, se activa la casilla Lápiz, se elige el color, → se pulsa el botón Aplicar
Gira -90º → se pulsa el botón Aplicar
Mueve 100 → se pulsa el botón Aplicar
Gira -90º → se pulsa el botón Aplicar
Mueve 100 → se pulsa el botón Aplicar
Gira -90º → se pulsa el botón Aplicar
Mueve 100 → se pulsa el botón Aplicar
- Para trazar un hexágono de lado 100 unidades se procede del siguiente modo
Se pulsa el botón titulado Nuevo, para borrar la trayectoria anterior. Y a continuación, se ejecuta la siguiente serie de comandos
Inicia X: 0, Y:100 → se pulsa el botón Aplicar
Gira -30º → se pulsa el botón Aplicar
Mueve 100, se activa la casilla Lápiz, se elige el color, → se pulsa el botón Aplicar
Gira -60º → se pulsa el botón Aplicar
Mueve 100, → se pulsa el botón Aplicar
Gira -60º → se pulsa el botón Aplicar
Mueve 100, → se pulsa el botón Aplicar
Gira -60º → se pulsa el botón Aplicar
Mueve 100, → se pulsa el botón Aplicar
Gira -60º → se pulsa el botón Aplicar
Mueve 100, → se pulsa el botón Aplicar
Gira -60º → se pulsa el botón Aplicar
Mueve 100, → se pulsa el botón Aplicar
De este modo, podemos dibujar otras figuras geométricas sencillas.
La clase Tortuga
La clase Tortuga tiene los siguientes miembros datos.
- La posición del objeto tortuga x e y.
- Su orientación, angulo.
- El color del lápiz con el que pinta su trayectoria.
- El movimiento de la tortuga se representa mediante trazos rectilíneos en el contexto gráfico g.
Los constructores inicializan los miembros dato, con valores por defecto o explícitos
public class Tortuga {
double x;
double y;
double angulo; //radianes
Color color;
Graphics g;
public Tortuga(double x, double y, double angulo, Color color) {
this.x=x;
this.y=y;
this.angulo=angulo*Math.PI/180;
this.color=color;
}
public Tortuga() {
this.x=0.0;
this.y=0.0;
this.angulo=0.0;
this.color=Color.black;
}
La función miembro inicia, sitúa la tortuga en el origen, orientada hacia el Este (ángulo 0) y establece como color del lápiz el negro. Esta función proporciona, además, el contexto gráfico g, en el que se representan los movimientos de la tortuga.
public void inicia(Graphics g){
x=0.0;
y=0.0;
angulo=0.0;
color=Color.black;
this.g=g;
}
La función colorea cambia el color de dicho lápiz
public void colorea(Color color){
this.color=color;
}
La función miembro gira, cambia la orientación de la tortuga, sumándole a su orientación actual un determinado ángulo expresado en grados.
public void gira(double angulo){
this.angulo+=angulo*Math.PI/180;
}
La función miembro salta, cambia la posición actual de la tortuga, a otra especificada por las coordenadas x e y.
public void salta(double x, double y){
this.x=x;
this.y=y;
}
La tortuga también puede cambiar de posición saltando a lo largo de su dirección (angulo) una distancia determinada.
public void salta(double distancia){
double xx=x+distancia*Math.cos(angulo);
double yy=y-distancia*Math.sin(angulo);
salta(xx, yy);
}
La función traza es similar a salta, la única diferencia es que la tortuga dibuja con su lápiz el camino (segmento) que sigue para moverse de un punto a otro a lo largo de su dirección (angulo) una distancia especificada. Cuando llega al final del camino la tortuga actualiza su posición.
public void traza(double distancia){
double xx=x+distancia*Math.cos(angulo);
double yy=y-distancia*Math.sin(angulo);
g.setColor(color);
g.drawLine((int)xx, (int)yy, (int)x, (int)y);
salta(xx, yy);
}
Fractales
El término fractal proviene de la palabra latina "fractus" y que se acuñó a finales de la década de los 70 por el matemático Benoit Mandelbrot.
Un fractal consta de fragmentos geométricos de orientación y tamaño variable, pero de aspecto similar. Si lo ampliamos nos irá mostrando una serie repetitiva de niveles de detalle, de modo que a todas las escalas que se examine, la estructura presentada será similar.
Para representar un fractal basta con crear una rutina que tome una forma geométrica simple y la dibuje a una determinada escala. Se repite varias veces la llamada a esta rutina de forma recursiva y a diferentes escalas.
Curva de Koch
En la generación del copo de nieve de Koch podemos ver que cada segmento es sustituido por cuatro segmentos cada uno de ellos de un tercio de la longitud del anterior.
La función recursiva que genera la curva de Koch la podemos ver en la figura para el nivel 0 (en la parte inferior) y para el nivel 1 (en la parte superior), y la podemos dibujar en el applet de la geometría de la tortuga. Recordar que para empezar un dibujo se pulsa el botón titulado Nuevo, y para ejecutar un comando hay que pulsar el botón Aplicar.
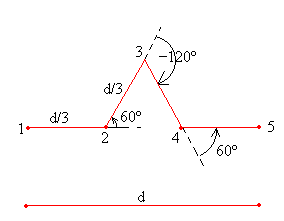 |
Inicia X:-120, Y: 0 Mueve 80 Gira 60º Mueve 80 Gira -120º Mueve 80 Gira 60º Mueve 80 |
El código de la función recursiva generaKoch que nos traza la curva de Koch es la siguiente
void generaKoch(int nivel, double distancia){
if(nivel==0){
tortuga.traza(distancia);
}else{
generaKoch(nivel-1, distancia/3);
tortuga.gira(60.0);
generaKoch(nivel-1, distancia/3);
tortuga.gira(-120.0);
generaKoch(nivel-1, distancia/3);
tortuga.gira(60.0);
generaKoch(nivel-1, distancia/3);
}
}
Para obtener la figura cerrada, se ejecuta el procedimiento generaKoch en cada uno de los tres segmentos de longitud d que forman un triángulo equilátero tal como se ve en la figura.
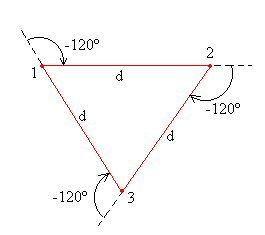 |
void curvaKoch(){
double distancia=(double)(3*wAlto-30)/(2*1.732);
double x=wAncho/2-distancia/2;
double y=(distancia/3)*1.732/2+5;
tortuga.salta(x, y);
generaKoch(orden, distancia);
tortuga.gira(-120);
generaKoch(orden, distancia);
tortuga.gira(-120);
generaKoch(orden, distancia);
}
|
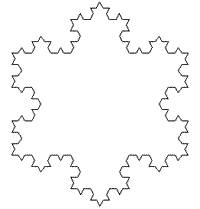
En las siguientes figuras, se muestra las primeras etapas en la generación de la curva de Koch.
 |
 |
 |
Curva de Peano
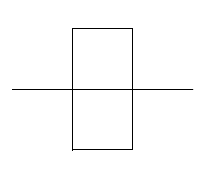
La función recursiva que genera la curva de Peano la podemos ver en la figura para el nivel 0 (en la parte inferior) y para el nivel 1 (en la parte superior), y la podemos dibujar en el applet de la geometría de la tortuga. Recordar que para empezar un dibujo se pulsa el botón titulado Nuevo, y para ejecutar un comando hay que pulsar el botón Aplicar.
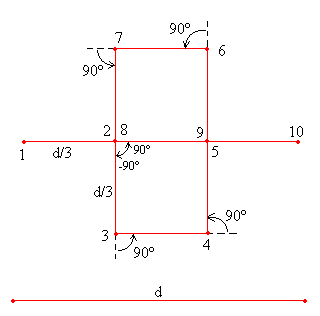 |
Inicia X:-120, Y: 0 Mueve 80 Gira -90º Mueve 80 Gira 90º Mueve 80 Gira 90º Mueve 80 Mueve 80 Gira 90º Mueve 80 Gira 90º Mueve 80 Gira 90º Mueve 80 Mueve 80 |
El código de la función recursiva generaPeano que nos traza la curva de Peano es la siguiente
void generaPeano(int nivel, double distancia){
if(nivel==0)
tortuga.traza(distancia);
else{
generaPeano(nivel-1, distancia/3);
tortuga.gira(-90.0);
generaPeano(nivel-1, distancia/3);
tortuga.gira(90.0);
generaPeano(nivel-1, distancia/3);
tortuga.gira(90.0);
generaPeano(nivel-1, distancia/3);
generaPeano(nivel-1, distancia/3);
tortuga.gira(90.0);
generaPeano(nivel-1, distancia/3);
tortuga.gira(90.0);
generaPeano(nivel-1, distancia/3);
tortuga.gira(90.0);
generaPeano(nivel-1, distancia/3);
generaPeano(nivel-1, distancia/3);
}
}
La llamada a esta función generaPeano comienza situando la tortuga en el punto inicial x, y, mediante la llamada a la función miembro salta.
void curvaPeano(){
double distancia=wAlto;
double x=wAncho/2-wAlto/2;
double y=wAlto/2;
tortuga.salta(x, y);
generaPeano(orden, distancia);
}
En las siguientes figuras, se muestra las primeras etapas en la generación de la curva de Peano
 |
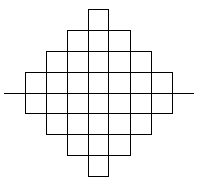 |
 |
Curva de Hilbert
Curva de Hilbert de orden cero la podemos generar como sigue en el applet de la geometría de la tortuga. Recordar que para empezar un dibujo se pulsa el botón titulado Nuevo, y para ejecutar un comando hay que pulsar el botón Aplicar
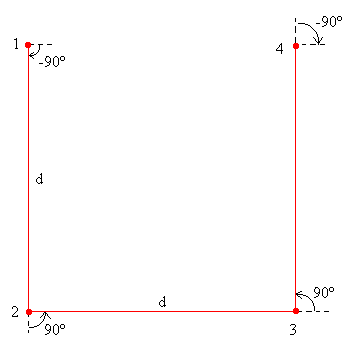 |
Inicia X:-50, Y: 50 |
Como podemos ver en las figuras, cada segmento se sustituye por otros cuatro de longitud mitad. El procedimiento recursivo es sin embargo, mucho más complejo que en los casos anteriores.
void generaHilbert(int nivel, int direccion, double distancia){
if(nivel>0){
tortuga.gira(-90*direccion);
generaHilbert(nivel-1, -direccion, distancia);
tortuga.traza(distancia);
tortuga.gira(90*direccion);
generaHilbert(nivel-1, direccion, distancia);
tortuga.traza(distancia);
generaHilbert(nivel-1, direccion, distancia);
tortuga.gira(90*direccion);
tortuga.traza(distancia);
generaHilbert(nivel-1, -direccion, distancia);
tortuga.gira(-90*direccion);
}
}
La llamada a la función recursiva generaHilbert comienza situando la tortuga en un punto inicial x, y, mediante la función miembro salta.
void curvaHilbert(){
double distancia=wAlto-10;
double x=wAncho/2-wAlto/2;
double y=5.0; // 5 de margen
tortuga.salta(x, y);
generaHilbert(orden+1, 1, distancia/(potencia2(orden+1)-1));
}
La función auxiliar potencia2, halla la potencia n de 2 y es muy simple de programar
private long potencia2(int n){
long resultado=1;
for(int i=1; i<=n; i++){
resultado*=2;
}
return resultado;
}
Lo que observamos al final es una curva cuya longitud se hace cada vez más grande (tiende a infinito) en un recinto limitado. Tras un número suficientemente grande de iteraciones la curva pasará por cualquier punto del plano.
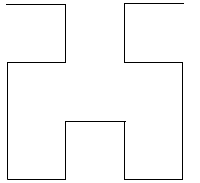
En las siguientes figuras, se muestra las primeras etapas en la generación de la curva de Hilbert.
 |
 |
 |
En el siguiente applet, se visualizan las primeras etapas de la generación de las curvas de Koch, Peano y Hilbert. Se selecciona el nombre de la curva en el control selección y a continuación se pulsa la barra de desplazamiento para elegir el nivel deseado
Bibliografía
Barallo Calonge, Javier. Geometría Fractal, Algorítmica y representación. Anaya Multimedia (1993).
