Deducción de la fórmula del efecto Doppler
A partir de la observación del movimiento del emisor, del observador y de los sucesivos frentes de onda, vamos a obtener la fórmula que describe el efecto Doppler.
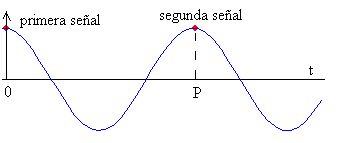
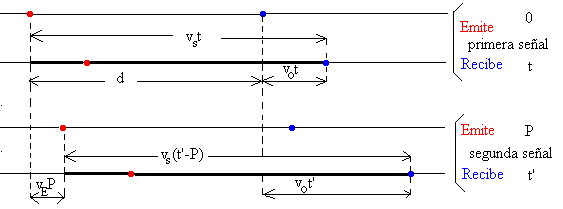
En la parte superior de la figura, tenemos dos señales, que pueden corresponder a dos picos consecutivos de una onda armónica, separados un periodo P. En la parte inferior, los dos puntos coloreados representan las posiciones del emisor (en rojo) y del observador (en azul). En el instante inicial t=0 en el que se emite la primera señal, el emisor y el observador están separados una distancia d desconocida, que no afecta al fenómeno en cuestión.
La primera señal es recibida por el observador en el instante t. La señal se desplaza el camino marcado en trazo grueso negro en la parte superior de la figura, desde que se emite hasta que se recibe, podemos por tanto, escribir la ecuación
vs·t=d+vO·t
La segunda señal se emite en el instante P, y se recibe en el instante t’. En el intervalo de tiempo entre la primera y la segunda señal, el emisor se desplaza vEP. La segunda señal recorre desde que se emite hasta que se recibe, el camino señalado en trazo grueso negro en la parte inferior de la figura. Por tanto, podemos escribir la ecuación
d-vE·P+vO·t’=vs·(t’-P)
Eliminando la cantidad desconocida d entre las dos ecuaciones, relacionamos el periodo P’=t’-t, de las ondas recibidas, con el periodo P de las ondas emitidas.
Teniendo en cuenta que la frecuencia es la inversa del periodo, obtenemos la relación entre frecuencias, o fórmula del efecto Doppler.
Ejercicio:
Un silbato emite sonido de frecuencia 500 Hz se mueve con una máquina de tren a velocidad de 90 km/h. Un conductor se mueve en la misma dirección pero en sentido contrario en un vehículo con una velocidad de 144 km/h acercándose al tren. Calcular la frecuencia del sonido escuchado por el conductor
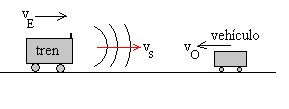 |
vE=25 m/s vs=340 m/s vO=-40 m/s La frecuencia del sonido escuchado es f'= 603 Hz |
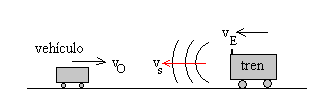 |
vE=-25 m/s vs=-340 m/s vO=40 m/s La frecuencia del sonido escuchado es f ' =603 Hz |
Procedimiento geométrico para dibujar los sucesivos frentes de onda
En el applet que viene a continuación, se muestra el procedimiento geométrico para dibujar con la regla y el compás los sucesivos frentes de onda, del sonido emitido por un vehículo en movimiento.
- Se dibuja una línea horizontal proporcional a la velocidad vE del emisor.
- Con el mismo origen, se dibuja una línea vertical proporcional a la velocidad del sonido vs
- Se unen los extremos de ambas líneas, formando un triángulo rectángulo
- Se divide la línea horizontal en varias partes iguales, poniendo una marca en cada una de las divisiones
- Se traza una línea vertical desde la marca hasta su intersección con la hipotenusa del triángulo rectángulo.
- Con centro en la marca y radio igual a la longitud de dicha línea vertical, se traza una circunferencia
- Se procede de la misma manera con todas las marcas de la línea horizontal.
Nota: Cuando vE > vs la hipotenusa del triángulo no es la envolvente de los sucesivos frentes de onda .
Actividades
Se introduce
- La velocidad del emisor vE proporcional a la velocidad vs del sonido
Se pulsa el botón titulado Empieza
Comienza una animación que muestra el procedimiento geométrico para dibujar los sucesivos frentes de ondas del sonido emitido por un vehículo en movimiento.
Referencias
Alt R., Wiley S., A generalized wave diagram for moving sources. The Physics Teacher Vol 42, December 2004, pp. 526-527
