Difracción de Fresnel

El propósito de esta página, es suscitar el interés del lector por los fenómenos de difracción.

La difracción de Fresnel se produce cuando la fuente puntual de ondas incidentes o el punto de observación desde el cual se las ve, o ambos, están a una distancia finita de la abertura o del obstáculo.

La difracción Fresnel es matemáticamente compleja especialmente la abertura circular. Algunos situaciones se pueden resolver de forma gráfica mediante la espiral de Cornu. En esta página, no se explica la difracción Fresnel, pero se recomienda la lectura del libro titulado.

Hecht E., Zajac A. Óptica. Editorial Addison-Wesley Iberoamericana (1986), págs. 388-418

Las integrales de Fresnel

Las integrales de Fresnel se definen

$\begin{array}{l} C (u) = \int_{0}^{u} \cos (\frac{π x^{2}}{2}) d x \\ S (u) = \int_{0}^{u} \sin (\frac{π x^{2}}{2}) d x \end{array}$

Estas integrales se pueden escribir de la forma

$\begin{array}{l} C (u) = \frac{1}{2} + f (u) \sin (\frac{π u^{2}}{2}) - g (u) \cos (\frac{π u^{2}}{2}) \\ S (u) = \frac{1}{2} - f (u) \cos (\frac{π u^{2}}{2}) - g (u) \sin (\frac{π u^{2}}{2}) \end{array}$

donde las funciones auxiliares f(u) y g(u) tienen las siguientes aproximaciones racionales, véase el primer artículo citado en las referencias

$\begin{array}{l} f (u) = \frac{1 + 0.926 u}{2 + 1.792 u + 3.104 u^{2}} \\ g (u) = \frac{1}{2 + 4.142 u + 3.492 u^{2} + 6.670 u^{3}} \end{array}$

La espiral de Cornu, es una curva que se obtiene dando valores al parámetro u. A continuación, se unen los puntos cuya abscisa es C(u) y cuya ordenada es S(u).

En los tres primeros applets, se indica el procedimiento geométrico para el cálculo de la intensidad debida a la difracción producida por

Una abertura rectangular
El borde de una placa semiinfinita
Un obstáculo en forma de placa rectangular

La abertura circular es la situación que tiene más importancia práctica. En el último applet, se muestra la intensidad debida a la difracción de una abertura circular: El cálculo de la intensidad se efectúa en términos de series convergentes de funciones de Bessel.

Difracción producida por una rendija

Se observa la evolución desde la difracción Fresnel a la difracción Fraunhofer a medida que se disminuye la anchura de la rendija.

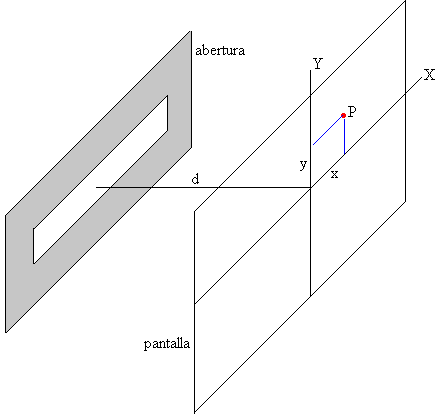
Arrastre el pequeño cuadrado de color rojo con el puntero del ratón

Referencias

Klein, Martin. Fresnel integrals. Am. J. Phys. 45 (3) March 1977, pp. 298-299

Press W. H., Teukolsky S. A., Vetterling W. T., Flannery B. P. Numerical Recipes in C, Second edition, Special functions. Fresnel Integrals, Cosine and Sine Integrals Chapter 6º. Cambridge University Press. Código en C adaptado por el autor al lenguaje Java