Movimiento de péndulos no acoplados de distinta longitud

En esta página, se simula el movimiento ondulatorio con péndulos no acoplados de distinta longitud.

Supongamos un conjunto de péndulos no acoplados de longitud variable, separados la misma distancia d, tal como se muestra en la figura.

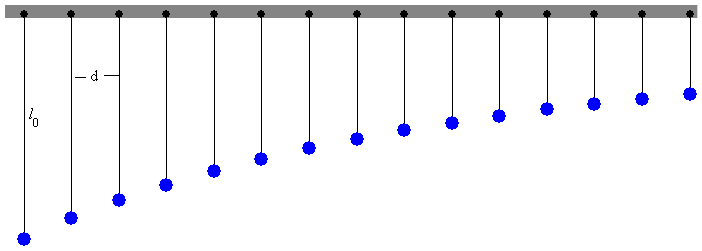
El primer péndulo se encuentra en la posición x=0, tiene una longitud l₀ describe N oscilaciones en el tiempo Γ
El segundo péndulo se encuentra en la posición x=d, tiene una longitud l₁, describe N+1 oscilaciones en el mismo tiempo Γ.
El tercer péndulo se encuentra en la posición x=2d, tiene una de longitud l₂, describe N+2 oscilaciones en el mismo tiempo Γ.
El péndulo n+1 se encuentra en la posición x=nd, tiene una de longitud l_n, describe N+n oscilaciones en el mismo tiempo Γ.

Descripción

El periodo T₀ y la longitud l₀ del primer péndulo son

$T_{0} = \frac{Γ}{N} l_{0} = \frac{g}{4 π^{2}} T_{0}^{2} = \frac{g}{4 π^{2}} \frac{Γ^{2}}{N^{2}}$

El periodo y la longitud del péndulo que se encuentra en la posición x=nd son

$T_{n} = \frac{Γ}{N + n} l_{n} = \frac{g}{4 π^{2}} T_{n}^{2} = \frac{g}{4 π^{2}} \frac{Γ^{2}}{{(N + n)}^{2}} n = 0, 1, 2 ...$

Si todos los péndulos se desplazan el mismo ángulo de su posición de equilibrio y se sueltan en el instante t=0.

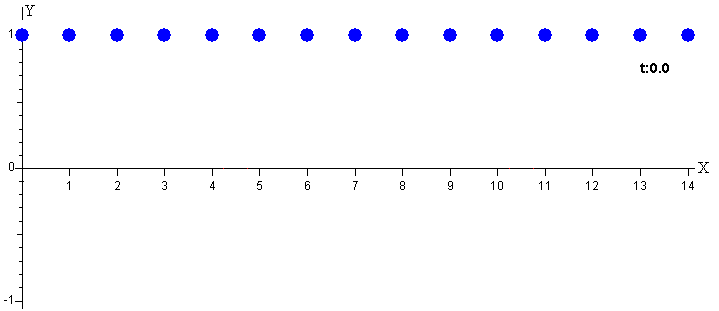
Cada uno de ellos describe un MAS de frecuencia angular ω_n=2π/T_n

y_n=A·cos(ω_n·t) n=0, 1, 2…

Las diferencia de fase entre dos péndulos adyacentes va creciendo con el tiempo, en el instante t=Γ/2 la diferencia de fase es constante

$Δ ϕ = ω_{n + 1} t - ω_{n} t = (\frac{2 π (N + (n + 1))}{Γ} - \frac{2 π (N + n)}{Γ}) \frac{Γ}{2} = π$

Si primer péndulo n=0, está en la posición y=+A (si N es par), el segundo péndulo estará en la posición y=-A, el tercero en la posición y=+A y así, sucesivamente.

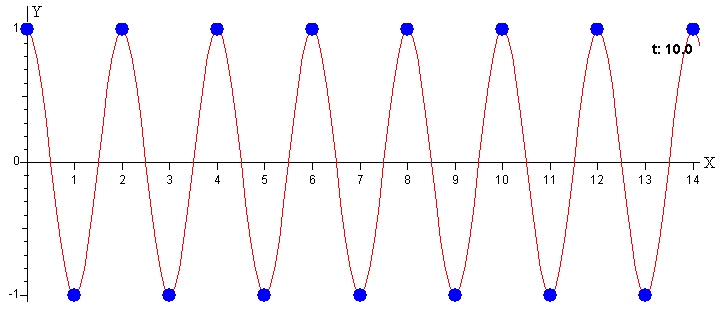
En el instante t=Γ todo los péndulos regresan a la posición de partida.

La función que describe la posición de cada unos de los péndulos en función del tiempo es

$y_{n} = A \cos (\frac{2 π (N + n)}{Γ} t) = A \cos (\frac{2 π (N d + x_{n})}{Γ d} t) = A \cos (\frac{2 π t}{Γ d} x_{n} + \frac{2 π N}{Γ} t)$

que tiene la forma de la propagación de una onda armónica y=Acos(kx+ωt) a lo largo del eje X y hacia la izquierda.

$k = \frac{2 π}{Γ d} t ω = \frac{2 π N}{Γ}$

El número de onda k y por tanto, la longitud de onda λ=2π/k= Γd/t no es constante. Es infinita para t=0 (todas las partículas están en una línea recta) y decrece con el tiempo.

El programa interactivo traza la función continua de x y t.

$y = A \cos (\frac{2 π t}{Γ d} x + \frac{2 π N}{Γ} t)$

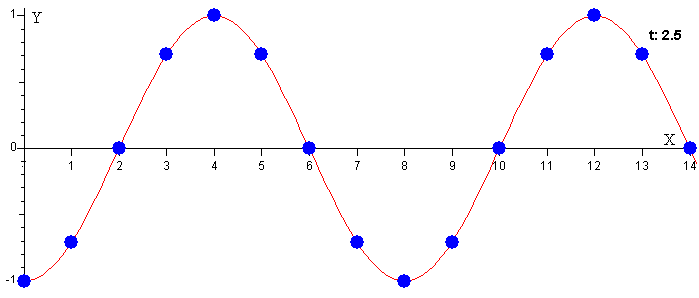
Sobre ella sitúa las posiciones y_n de cada una de las partículas en el instante t

$y_{n} = A \cos (\frac{2 π (N + n)}{Γ} t) n = 0, 1, 2,...$

En la figura, se muestra las posiciones de los péndulos en el instante t=Γ/8

Actividades

Se introduce

El número de oscilaciones N que describe el péndulo de mayor longitud, en el control d edición titulado N. oscilaciones
El tiempo Γ que tarda en describirlas, en el control de edición titulado en el tiempo

Se pulsa el botón titulado Nuevo

Se muestran 15 péndulos, y debajo de cada uno de ellos se proporciona el dato su periodo T_n en segundos

Se pulsa el botón titulado Empieza

Los 15 péndulos parten de la posición y=+1, en el instante t=0, los péndulos empiezan a oscilar, podemos observar ciertos instantes en los que parecen formar una estructura ordenada de una onda que se propaga, en otros, de una onda estacionaria y otros instantes, las posiciones de los péndulos parecen adoptar una estructura caótica.

LibresApplet aparecerá en un explorador compatible con JDK 1.1.

Referencias

Flaten J. A. Parendo K. A., Pendulum waves: A lesson in aliasing. Am. J. Phys. 69 (7) July 2001, pp. 778-782