Órbitas elípticas bajo la acción de la fuerza central –k·r

Consideremos el movimiento de una partícula de masa m bajo la acción de una fuerza atractiva cuyo módulo proporcional a la distancia al centro de fuerzas.

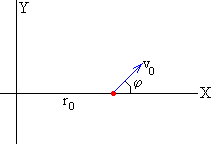
Vamos a determinar la ecuación de su trayectoria sabiendo que la partícula parte de la posición (r₀, 0) con velocidad v₀ haciendo un ángulo φ con el eje X, tal como se muestra en la figura.

Ecuación del movimiento

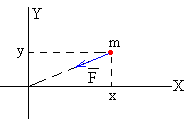Cuando la partícula se encuentra en la posición r(x, y), la fuerza que actúa sobre la partícula es –k·r=-kxi-kyj

La ecuación del movimiento de la partícula es:

$m \frac{d^{2} r}{d t^{2}} = - k r {\begin{cases} m \frac{d^{2} x}{d t^{2}} = - k x \\ m \frac{d^{2} y}{d t^{2}} = - k y \end{cases}$

La solución de este sistema de dos ecuaciones diferenciales es:

$\begin{array}{l} x = A \sin (ω t + δ_{1}) \\ y = B \sin (ω t + δ_{2}) \end{array}} ω = \sqrt{\frac{k}{m}}$

Que es la composición de dos MAS de la misma frecuencia y direcciones perpendiculares

Las componentes de la velocidad de la partícula son

$\begin{array}{l} \frac{d x}{d t} = A ω \cos (ω t + δ_{1}) \\ \frac{d y}{d t} = B ω \cos (ω t + δ_{2}) \end{array}$

Las amplitudes A y B y las fases iniciales δ₁ y δ₂ se determinan a partir de las condiciones iniciales, en el instante t=0, la partícula parte de la posición x=r₀, y=0, con velocidad v_x=v₀·cosφ, v_y=v₀·sinφ.

Tenemos el siguiente sistema de ecuaciones para despejar las amplitudes A y B, y las fases iniciales δ₁ y δ₂

r₀=Asinδ₁
v₀·cosφ= Aωcosδ₁
0=Asinδ₂
v₀·sinφ= Bωcosδ₂

Despejamos las incógnitas

$\begin{array}{l} δ_{2} = 0 B = \frac{v_{0}}{ω} \sin ϕ \\ δ_{1} = \arctan (\frac{ω}{v_{0}} \frac{r_{0}}{\cos ϕ}) A = \sqrt{r_{0}^{2} + {(\frac{v_{0}}{ω} \cos ϕ)}^{2}} \end{array}$

Eliminando el tiempo t obtenemos la ecuación de la trayectoria

$\begin{array}{l} x = A \sin (ω t) \cos δ_{1} + A \cos (ω t) \sin δ_{1} \\ x - A \sin (ω t) \cos δ_{1} = A \cos (ω t) \sin δ_{1} \end{array}$

Elevando al cuadrado ambos miembros

$\begin{array}{l} x^{2} + A^{2} \sin^{2} (ω t) \cos^{2} δ_{1} - 2 A x \sin (ω t) \cos δ_{1} = A^{2} \cos^{2} (ω t) \sin^{2} δ_{1} \\ x^{2} + A^{2} \sin^{2} (ω t) - 2 A x \sin (ω t) \cos δ_{1} = A^{2} \sin^{2} δ_{1} \\ x^{2} + A^{2} \frac{y^{2}}{B^{2}} - 2 x \frac{y}{B} A \cos δ_{1} = r_{0}^{2} \\ x^{2} + \frac{r_{0}^{2} ω^{2} + v_{0}^{2} \cos^{2} ϕ}{v_{0}^{2} \sin^{2} ϕ} y^{2} - \frac{2 x y}{\tan ϕ} = r_{0}^{2} \end{array}$

La ecuación de la trayectoria depende del ángulo φ con el que se dispara la partícula.

f(x, y, φ)=0

La envolvente

La ecuación de la envolvente de las trayectorias se obtiene derivando con respecto a φ e igualando a cero.

$\begin{array}{l} \frac{\partial f}{\partial ϕ} = 0 \\ - \frac{2 \cos ϕ (r_{0}^{2} ω^{2} + v_{0}^{2})}{v_{0}^{2} \sin^{3} ϕ} y^{2} + 2 x y \frac{1}{\sin^{2} ϕ} = 0 \\ \tan ϕ = \frac{y}{x} \frac{(ω^{2} r_{0}^{2} + v_{0}^{2})}{v_{0}^{2}} \end{array}$

y combinando ésta con la ecuación de la trayectoria para eliminar el ángulo φ. Para ello, empleamos las relaciones trigonométricas

$\begin{array}{l} \cos^{2} ϕ = \frac{1}{1 + \tan^{2} ϕ} = \frac{v_{0}^{4} x^{2}}{v_{0}^{4} x^{2} + {(ω^{2} r_{0}^{2} + v_{0}^{2})}^{2} y^{2}} \\ \sin^{2} ϕ = \frac{\tan^{2} ϕ}{1 + \tan^{2} ϕ} = \frac{{(ω^{2} r_{0}^{2} + v_{0}^{2})}^{2} y^{2}}{v_{0}^{4} x^{2} + {(ω^{2} r_{0}^{2} + v_{0}^{2})}^{2} y^{2}} \end{array}$

Introducimos las expresiones de sin²φ, cos²φ y tanφ en la ecuación de la trayectoria obteniendo la ecuación de la envolvente, que es una elipse de semiejes a y b.

$\begin{array}{l} \frac{ω^{2}}{v_{0}^{2} + ω^{2} r_{0}^{2}} x^{2} + \frac{ω^{2}}{v_{0}^{2}} y^{2} = 1 \\ a = \sqrt{r_{0}^{2} + \frac{v_{0}^{2}}{ω^{2}}} b = \frac{v_{0}}{ω} \end{array}$

Actividades

Se introduce

La posición r₀ de disparo de la partícula, actuando en la barra de desplazamiento titulada Posición.
La velocidad de disparo v₀, actuando en la barra de desplazamiento titulada Velocidad.
Se ha fijado la frecuencia angular ω=1

Se pulsa el botón titulado Empieza

Se observa las trayectorias de las partículas disparadas con ángulos φ=0º, 30º, 60º, 90º, 120º, 150º, 180º, 210º, 240º, 270º, 300º, 330º y la envolvente de todas las trayectorias elípticas.

Referencias

French A. P. The envelopes of some families of fixed-energy trajectories. Am. J. Phys. 61 (9) September 1993