Una partícula que cae sobre un muelle elástico

Consideremos el siguiente sistema oscilante. Una partícula de masa m, se deja caer desde una altura h, sobre una plataforma de masa M unida a un muelle elástico, de constante k. En una primera aproximación, consideremos que la plataforma tiene masa despreciable. La partícula cae sobre el muelle elástico, lo deforma y rebota, volviendo a la posición inicial de partida. El sistema es conservativo.

En la página titulada “Choque inelástico entre un bloque que cae y una plataforma que descansa sobre un muelle elástico” se ha estudiado el caso de que M≠0 y el choque sea completamente inelástico y la partícula quede pegada a la plataforma después del choque.

Ecuaciones del movimiento

Estudiamos las distintas etapas del movimiento de la partícula, para ello establecemos el origen en la posición de la plataforma en reposo, tal como se muestra en las figuras. Vamos a disponer de dos relojes uno que mide el tiempo parcial t de cada una de las etapas del movimiento y otro que mide el tiempo total tt, desde el momento en el que se libera la partícula a una altura h sobre el origen.

1.-Caída libre x≥0

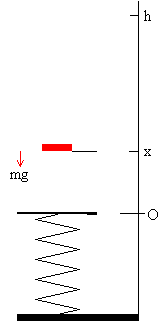La partícula se suelta a una altura h en el instante t=0, tt=0.

La posición y velocidad de la partícula es

$x = h - \frac{1}{2} g t^{2} v = - g t$

La partícula tarda en llegar al origen x=0 un tiempo t₁ (instante tt=t₁) alcanzando una velocidad v₁

$t_{1} = \sqrt{\frac{2 h}{g}} v_{1} = - \sqrt{2 g h}$

2.-La partícula deforma el muelle, x≤0

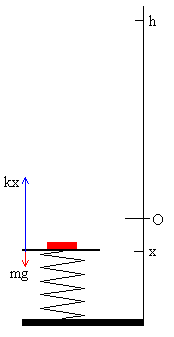Las fuerzas sobre la partícula son el peso y la fuerza que ejerce el muelle. La segunda ley de Newton se escribe

ma=-kx-mg

(como x≤0, –kx≥0 es positiva, tal como se muestra en la figura)

En forma de ecuación diferencial

$\frac{d^{2} x}{d t^{2}} + \frac{k}{m} x = - g \frac{d^{2} x}{d t^{2}} + ω^{2} x = - g$

La solución de esta ecuación diferencial es la suma de la solución de la ecuación diferencial homogénea

x₁=Asin(ωt)+Bcos(ωt)

donde A y B son constantes que se determinan a partir de las condiciones iniciales

y de la solución particular

x₂=C

introduciendo la solución particular en la ecuación diferencial determinamos el valor de la constante C.

ω²C=-g

La solución de la ecuación diferencial completa es x=x₁+x₂

$\begin{array}{l} x = - \frac{g}{ω^{2}} + A sin (ω t) + B \cos (ω t) \\ v = \frac{d x}{d t} = A ω cos (ω t) - B ω sin (ω t) \end{array}$

Las condiciones iniciales son las siguientes: la partícula unida al muelle elástico parte en el instante t=0 (tiempo total tt=t₁) del origen x=0, con velocidad v₁. Resolvemos el sistema de dos ecuaciones con dos incógnitas

$B = \frac{g}{ω^{2}} = \frac{m g}{k} A = \frac{- \sqrt{2 g h}}{ω} = - \sqrt{\frac{2 m g h}{k}}$

El máximo desplazamiento de la partícula se alcanza en el instante t₂ cuando v=0,

$\tan (ω t) = \frac{A}{B} = - \sqrt{\frac{2 h k}{m g}} t_{2} = \sqrt{\frac{m}{k}} (π - \arctan (\sqrt{\frac{2 h k}{m g}}))$

y vale

$\begin{array}{l} x_{m} = - \frac{m g}{k} - \sqrt{\frac{2 m g h}{k}} sin (ω t_{2}) + \frac{m g}{k} \cos (ω t_{2}) \\ x_{m} = - \frac{m g}{k} (1 + \sqrt{1 + \frac{2 h k}{m g}}) \end{array}$

Para obtener esta expresión, se emplean las relaciones trigonométricas,

$\cos θ = \frac{1}{\sqrt{1 + \tan^{2} θ}} sin θ = \frac{\tan θ}{\sqrt{1 + \tan^{2} θ}}$

como ωt₂ es un ángulo del segundo cuadrante, el seno es positivo y el coseno es negativo.

El tiempo que tarda en la partícula desde que parte del origen y regresa al origen es

T_v=2t₂

Podemos comprobar haciendo algunas operaciones, que en el instante t=2t₂, la posición de la partícula es x=0 y su velocidad es $\sqrt{2 g h}$

Para ello, se utilizan las relaciones trigonométricas

cos(2θ)=cos²θ-sin²θ
sen(2θ)=2cosθ·sinθ

y las dos que relacionan el seno y el coseno con la tangente,

3.-La partícula asciende

La partícula sale del origen con velocidad $\sqrt{2 g h}$ en el instante t=0, (tiempo total tt=t₁+2t₂)

La posición y velocidad de la partícula son

$x = \sqrt{2 g h} t - \frac{1}{2} g t^{2} v = \sqrt{2 g h} - g t$

Alcanza la máxima altura cuando v=0, y tarda un tiempo t₃ en alcanzarla

$t_{3} = \sqrt{\frac{2 h}{g}}$

es decir, su posición en el instante tt=t₁+2t₂+t₃=2t₁+2t₁ es x=h, la de partida

El tiempo total P (periodo de la oscilación), que emplea la partícula desde que parte hasta que llega es

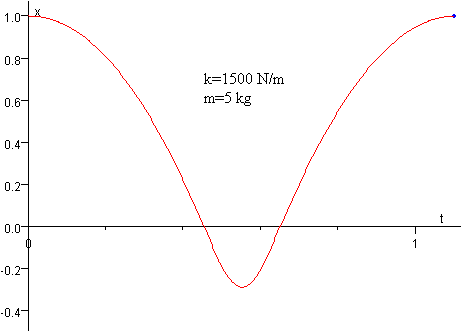
$P = 2 \sqrt{\frac{2 h}{g}} + 2 \sqrt{\frac{m}{k}} (π - \arctan (\sqrt{\frac{2 h k}{m g}}))$

En la figura, se muestra la posición x de la partícula en función del tiempo total tt, durante un periodo T de oscilación

Energía de la partícula

La energía potencial de la partícula es

$E_{p} (x) = {\begin{cases} m g x + \frac{1}{2} k x^{2} x \leq 0 \\ m g x x \geq 0 \end{cases}$

La energía total de la partícula es E=mgh, se convierte en cinética cuando pasa por el origen x=0. Cuando x<0 el muelle se deforma y la velocidad v de la partícula es

$m g h = \frac{1}{2} m v^{2} + m g x + \frac{1}{2} k x^{2}$

La velocidad se hace cero en la posición, raíz de la ecuación de segundo grado en x.

$x_{m} = \frac{- m g - \sqrt{m^{2} g^{2} + 2 k m g h}}{k} = - \frac{m g}{k} (1 + \sqrt{1 + \frac{2 k h}{m g}})$

En la figura se muestra, la partícula en una posición x. El segmento horizontal representa la energía total, el segmento vertical AB es la energía potencial y el segmento BC es la energía cinética. La partícula se mueve en el intervalo x_m≤x≤h. en el cual la energía cinética es mayor o igual a cero. Las posiciones x_m y h se denominan de retorno porque la velocidad de la partícula en estos dos puntos es cero, partícula cambia la dirección de su velocidad.

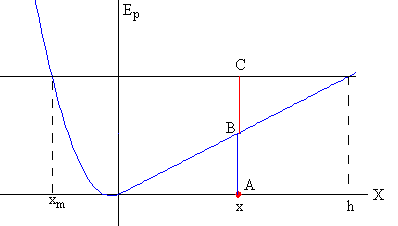
La fuerza sobre la partícula es la pendiente de la recta tangente cambiada de signo. La pendiente a la derecha del origen es constante.

$F = - \frac{d E_{p} (x)}{d x} = {\begin{cases} - m g x \leq 0 \\ - m g - k x x \geq 0 \end{cases}$

La energía potencial presenta un mínimo en el intervalo x≤0. Se trata de una posición de equilibrio estable.

x_e=-mg/k

El peso se iguala a la fuerza que ejerce el muelle elástico

Ejemplo.

Masa de la partícula m=5 kg
Constante elástica del muelle k=1500 N/m
El bloque parte de la posición h=1 m con velocidad v=0.

El bloque cae, y llega al origen x=0, en el instante tt=t₁=0.452 s, alcanzando una velocidad v₁=4.43 m/s.

La partícula entra en contacto con el muelle elástico. La deformación del muelle es máxima cuando la velocidad de la partícula v=0. Esto sucede en el instante tt=t₁+t₂

$t_{2} = \sqrt{\frac{m}{k}} (π - \arctan (\sqrt{\frac{2 h k}{m g}})) t_{2} = \sqrt{\frac{5}{1500}} (π - \arctan (\sqrt{\frac{2 \cdot 1 \cdot 1500}{5 \cdot 9.8}})) = 0.098 s$

La partícula regresa al origen en el instante tt=t₁+2t₂=0.648 s

La partícula vuelve a la posición inicial de partida, completando un periodo en el instante tt=2t₁+2t₂=1.100 s

Actividades

Se introduce

La masa m de la partícula, en el control de edición titulado Masa partícula
La constante elástica del muelle k, en el control de edición titulado Constante elástica
La altura inicial desde la que se suelta la partícula es h=1 m

Se pulsa el botón titulado Inicio

El programa verifica si la máxima deformación del muelle x_m es inferior a 0.45 m, en cuyo caso se invita al usuario a disminuir la masa del bloque o a aumentar el valor de la constante elástica.

Se elige el tipo de diagrama que se desea visualizar, activando el botón de radio titulado:

Energía, se representa de la energía potencial E_p(x) en función d ela posición x de la partícula
x-t, se representa a posición x de la partícula en función del tiempo t
v-x, la velocidad v de la partícula en función de su posición x (espacio de las fases)

Se pulsa el botón titulado Empieza

Se observa el movimiento de la partícula, en la parte izquierda del applet, y la representación gráfica elegida en la parte derecha.

LibresApplet aparecerá en un explorador compatible con JDK 1.1.

Referencias

Lopac V., Dananic V. Energy conservation and chaos in the gravitationally driven Fermi oscillator. Am. J. Phys. 66 (10) October 1998, pp. 892-902